Logistic Regression(로지스틱 회귀)

1. 정의

이진 분류 문제를 해결하기 위한 대표적인 알고리즘으로, 기계 학습에서 로지스틱 회귀는 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측한 뒤 그 확률에 따라서 가능성이 특정 기준치(threshold) 이상인 경우 해당 클래스로 분류해 주는 지도학습 알고리즘입니다.

2. 이진 분류

60점 이상일 때 합격하는 시험의 합/불합 결과를 이진분류 한다고 했을 때 하나의 feature인 성적을 기준으로 진행할 경우 아래와 같이 분류가 될 수 있습니다.

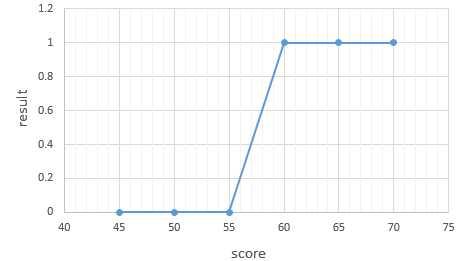
레이블에 해당하는 y에서 0을 불합격 1을 합격으로 간주할 시 y는 두 가지 값만을 가지므로, 이 문제를 풀기 위해서 예측값은 0과 1사이의 값을 가지도록 합니다. 이렇듯 s자 형태를 그리는 함수로 대표적인 함수는 후에 설명할 시그모이드 함수입니다.

p.s. 시그모이드 함수 외에도 클래스를 둘로 나눌 수만 있다면 그 어떤 함수를 이용해도 무방합니다.

3. 시그모이드 함수

$σ(z)={1 \over{1+e^{−z}}}$

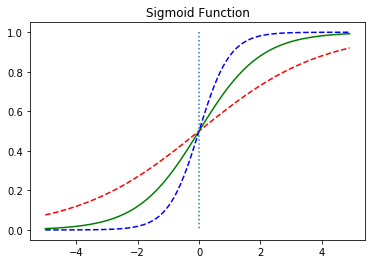
시그 모이드 함수는 위에서 볼 수 있듯 출력 값의 범위 0~1 사이이며, 경사하강법 시행 시에 기울기가 급격하게 변해서 발산하는 기울기 폭주가 발생하지 않는다는 장점이 있습니다. 하지만 출력되는 값의 범위가 좁아 기울기 소실 문제를 유발시킬 수 있다는 단점이 있습니다.

4. 왜 Regression(회귀)가 Classification(분류)에 사용되는가?

분명 logistic regression, 즉 결과값을 연속형으로 갖는 회귀 알고리즘인데 정작 용도는 classification이라는 점에서 의문이 들으셨을 수 있습니다. 그 이유는 2가지가 있습니다.

1. 이진 분류 문제의 자연스러운 적용이 가능

2. 분류 모델의 성능 향상에 기여할 수 있음

   로지스틱 회귀는 분류 모델의 성능 향상에 기여할 수 있습니다. 예측값과 실제값 사이의 오차는 로스 함수를 통해 계산되고, 이를 기반으로 경사 하강법 같은 최적화 알고리즘을 사용해 모델이 개선됩니다. 데이터 포인트들이 학습된 결정 경계를 기준으로 명확히 분류되는 방향으로 모델이 점진적으로 개선됩니다.

Reference

https://terms.naver.com/entry.naver?docId=6653422&cid=69974&categoryId=69974

https://wikidocs.net/35476

https://gooopy.tistory.com/52