VariationalAutoencoder(VAE)

유승한·2024년 10월 21일

딥러닝

목록 보기

11/15

1. VAE(VariationalAutoencoder)란?

VAE(Variational Autoencoder)는 확률적 접근을 사용하는 생성 모델로, 주어진 입력 데이터를 잠재 공간(latent space)으로 변환하고 그로부터 데이터를 재구성하는 데 사용됩니다. VAE는 일반적인 오토인코더(Autoencoder)의 변형이며, 데이터의 잠재 공간 분포를 학습하고 새로운 데이터를 생성하는 데 특화되어 있습니다.
오토인코더에 대해서 모르신다면 해당 포스트를 참고해주세요.

Prior Distribution, $p(z)$

p는 잠재변수 z가 따르는 사전 확률 분포를 의미합니다.
$z\sim p(z)$ : VAE에서 일반적으로 z는 정규분포 $N(0, I)$ 를 따르는 것으로 가정합니다.
- 잠재 변수 z 는 데이터의 숨겨진(잠재적인) 특성을 나타내는 변수로, 보통 VAE나 GAN에서는 정규 분포(또는 다른 사전 분포)에서 샘플링됩니다.

Generator, $g_{\theta}(z)$

생성자 $g_{\theta}(z)$ 는 잠재 변수 z 를 입력으로 받아 데이터 x 를 생성하는 함수입니다. $\theta$ 는 이 생성자의 파라미터를 나타냅니다.

$p(x|g_{\theta}(z))=p_{\theta}(x|z)$

$g_{\theta}(z)$ 는 잠재 변수 z 를 받아, 데이터를 생성하는 함수이기 때문에 x는 $g_{\theta}(z)$ 로 표현될 수 있습니다.
$p(x|g_{\theta}(z))$ 는 잠재 변수 z를 통해 생성된 데이터 x 의 조건부 확률입니다. 즉, z가 주어졌을 때 x가 생성될 확률을 나타냅니다.
이때, $g_{\theta}(z)$ 는 x를 생성하는 함수이므로, $p(x|g_{\theta}(z))$ 와 $p_{\theta}(x|z)$ 는 동일한 의미를 가집니다. 즉, $g_{\theta}(z)$ 가 주어진 데이터 x의 생성 확률을 표현하는 역할을 하기 때문에 두 표현은 같은 의미를 전달합니다.

vae가 학습을 통해 이루고자하는 목표는 train datapoint x가 나올 확률을 maximize하는 것입니다.

또한 단순히 샘플을 생성하는 것이 아닌 이미지를 조정하여 샘플을 생성하기 위해 컨트롤러를 이용하게 됩니다.

그 컨트롤러의 역할을 하는 것이 바로 Latent Space z입니다.

이때 prior distribution을 정규분포로 가정한 뒤, 샘플링을 진행할 시에 샘플링 된 값이 manifold를 대표하는 값을 가질 수 있는 이유는 아래 그림에서 확인할 수 있습니다.

깊은 신경망이기에, 한 두개의 레이어는 실제로 배워야할 복잡한 manifold를 잘 찾기 위해 사용될 수 있습니다.
위 사진은 간단한 함수가 적용되는 레이어로 데이터 분포를 간단히 할 수 있음을 표현합니다.

위 슬라이드에서 보여주는 MNIST 데이터셋의 세 이미지(a, b, c)를 보면, MSE 관점에서 a와 c(a에서 화소 한 개를 이동시킨 이미지)가 a와 b(a에서 일부분을 제거한 이미지)보다 MSE 값이 훨씬 큽니다. 즉, MSE 값이 작다고 해서 의미적으로 더 가까운 이미지를 나타내지는 않을 수 있습니다. 이는 단순한 MSE 기반의 손실 함수가 의미론적 유사성을 잘 포착하지 못할 수 있음을 보여줍니다.

따라서, 잠재 공간에서 샘플링을 할 때 학습이 제대로 이루어지기 어려울 수 있습니다. 이러한 문제를 해결하기 위해 도입된 것이 바로 Variational Inference입니다.

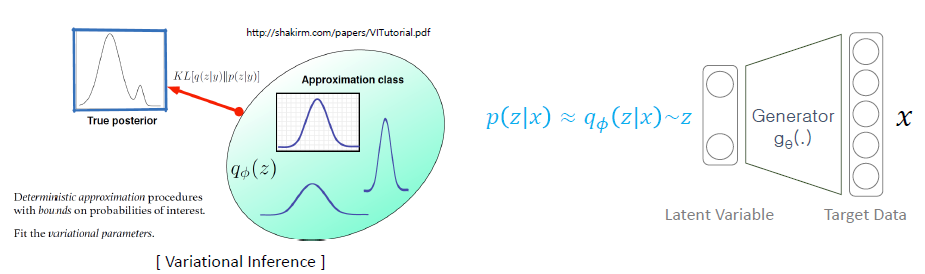
prior가 아닌 이상적인 샘플링 함수에서 샘플링을 진행하게 된다고 가정해봅시다. 이때 이상적인 z를 샘플링해내기 위해 x가 주어집니다. 이때 이상적인 샘플링 함수를 추정하기 위해 사용하는 것이 Variational Inference 방법입니다.

Variational Inference

우리가 다루기 쉬운(알고 있는) 함수분포 : ex) 가우시안 분포
확률분포를 결정짓는 파라미터 : $\phi$
변분 추론(Variational Inference)을 통해 $\phi$ 를 조정하여 근사 후방 분포 $q_{\phi}(z|x)$ 를 도출하고, 이를 통해 우리가 추정하려는 참된 후방 분포(True posterior)와 최대한 유사하게 만듭니다.

term 정리

true posterior: p(z|x) - how likely the latent variable is given the input
prior: p(z) - how the latent variables are distributed without any conditioning
approximation function(sampling function): q(z|x)

2. 수식

ELBO(Evidence LowerBOund)

우리가 궁극적으로 원하는 것은 훈련 데이터에 있는 입력 데이터와 유사한 분포를 가지는 샘플을 생성하는 것입니다. 이를 위해 p(x) 를 최적화합니다.

수식을 간단히하기 위해 log를 씌워줄 시에 p(x)에서 $ELBO(Φ)$ 값과 $KL(q_{Φ}(z|x)||p(z|x))$ 를 얻을 수 있습니다. 앞서 얘기했듯 p(x)를 최적화하기 위해 $ELBO(Φ)$ 의 최대로하는 Φ를 찾게됩니다. 그 이유는 $p(z|x)$ 를 모르기 때문에 $KL(q_{Φ}(z|x)||p(z|x))$ 을 직접적으로 최소화시키보다, $ELBO(Φ)$ 값을 최대로 하는 Φ를 찾는 것입니다.

ELBO 수식을 전개할 시에 위와 같이 도출됩니다. 결과적으로 아래와 같은 수식이 완성됩니다.

앞서 두 확률분포 간의 거리인 KL term은 계산을 할 수 없기에 앞에 ELBO를 최적화시켜줘야 한다고 언급했습니다. 따라서 우리가 최적화를 시켜야 할 값은 'Reconstruction term'과 'Regularization term'입니다.

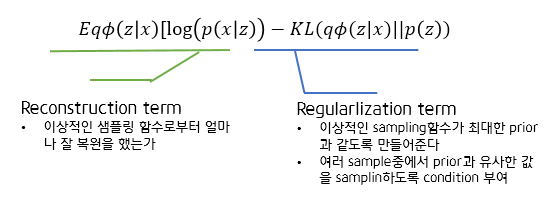
정리하자면 vae에게 요구하는 것은 크게 2가지입니다.

이상적인 샘플링 함수로 부터 생성한 z값으로부터 (Training DB에 있는) input data와 유사한 데이터를 생성해줘 ← Generation
이상적인 sampling함수의 값이 최대한 prior값과 같도록 만들어줘 ← Condition

이렇게 아래와 같은 VAE가 구성됩니다.

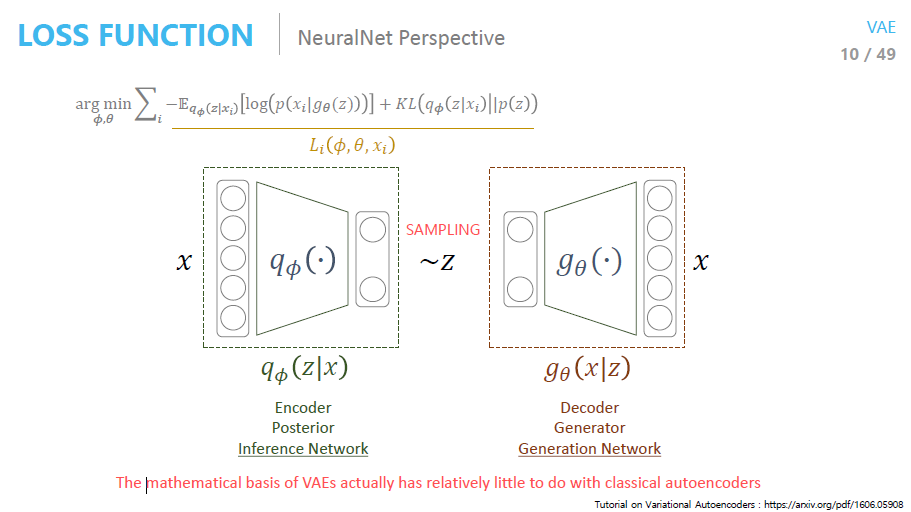
정리하자면, 우리의 목적은 생성자(Generator)를 학습시키는 것입니다. VAE는 생성 모델(generative model)이므로, 주어진 데이터를 기반으로 잠재 변수 z 에서 샘플링하여 데이터를 생성하는 능력을 학습합니다.

그러나 사전 분포(prior)만을 가지고 학습하면, 잠재 공간에서의 샘플링이 불충분하고 학습이 잘 되지 않습니다. 따라서 우리는 후방 분포를 근사하는 이상적인 샘플링 함수를 도입합니다.

이상적인 샘플링 함수는 바로 $q_\phi(z|x)$ 입니다. $q_\phi(z|x)$ 는 입력 데이터 x 가 주어졌을 때, 잠재 변수 z 를 샘플링하는 근사 후방 분포를 나타냅니다.

우리는 입력 데이터 x를 evidence로 주고, 그에 맞는 잠재 변수 z 를 샘플링하여 Generator가 데이터를 잘 복원할 수 있도록 학습합니다. 이 과정에서 $q_\phi(z|x)$ 가 z 를 샘플링하기 위한 함수로 도입됩니다.

샘플링된 잠재 변수 z를 통해 데이터를 복원하고, 그 결과가 입력 데이터 x 와 최대한 유사하도록 만드는 것이 목표입니다. 이를 재구성 항(Reconstruction Term)이라고 하며, 이 과정에서 최대 우도 추정(MLE) 문제로 파라미터 $\theta$ 를 최적화할 수 있습니다.

Φ에 대한 최적화: $\phi$ 는 인코더의 파라미터로, 근사 후방 분포 $q_\phi(z|x)$ 를 나타냅니다. ELBO를 $\phi$ 에 대해 최대화하는 것은 잠재 공간에서의 샘플링 함수를 최적화하여, 참된 후방 분포 $p(z|x)$ 에 최대한 가까운 분포를 학습하는 것을 의미합니다.
𝜃에 대한 최적화: $\theta$ 는 디코더의 파라미터로, 잠재 변수 z 로부터 데이터 x를 재구성하는 능력을 최적화합니다. 이 과정에서 최대 우도 추정(MLE) 관점에서 데이터를 잘 복원할 수 있는 네트워크 파라미터를 학습합니다.

따라서 ELBO는 VAE의 전체 학습 과정을 나타내는 중요한 최적화 함수이며, 인코더와 디코더의 파라미터를 각각 $\phi$ 와 $\theta$ 에 대해 최대화하여 VAE를 학습합니다.

3. Reparameterization Trick

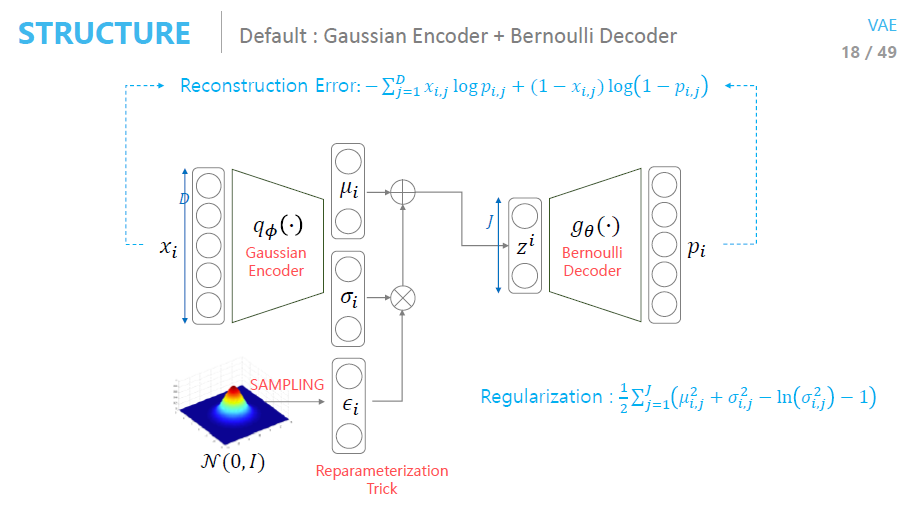
VAE는 입력 데이터를 잠재 공간에서 확률 분포로 표현합니다. 구체적으로, 인코더는 입력 데이터 x로부터 잠재 변수 z의 분포 매개변수(평균 $\mu$ 와 표준편차 $\sigma$ )를 예측합니다. 그 다음, 이 분포에서 잠재 변수 z를 샘플링한 후, 이를 디코더에 입력하여 데이터를 재구성합니다.

잠재 변수 z는 주어진 분포 $q_\phi(z|x$ )에서 샘플링되어야 합니다 : $z∼q_ϕ(z∣x)$

그러나, 샘플링 과정은 본질적으로 비미분 가능하므로, 경사 하강법과 같은 최적화 알고리즘을 사용할 수 없습니다. 이로 인해 인코더가 최적화 과정에서 학습하기 어려워집니다.

Reparameterization Trick은 잠재 변수 z를 샘플링하는 비미분 가능 과정을 미분 가능한 연산으로 변환하는 기법입니다. 구체적으로, 잠재 변수 z를 직접 샘플링하는 대신, 가우시안 노이즈를 활용해 잠재 변수 z를 재구성하는 방식입니다.

재매개변수화 트릭의 단계:

분포의 매개변수화: 인코더는 입력 데이터 x로부터 잠재 변수 z의 분포 매개변수인 평균 $\mu$ 와 표준편차 $\sigma$ 를 출력합니다.

$\mu = f_\mu(x), \quad \sigma = f_\sigma(x)$

여기서 $f_\mu(x)$ 와 $f_\sigma(x)$ 는 인코더 네트워크가 학습하는 함수입니다.
가우시안 샘플링: 잠재 변수 z는 평균 $\mu$ 와 표준편차 $\sigma$ 로부터 샘플링되는 가우시안 분포에서 얻어집니다. 직접 샘플링할 수 없으므로, 이를 다음과 같이 재구성합니다:

$z = \mu + \sigma \cdot \epsilon, \quad \epsilon \sim \mathcal{N}(0, I)$

여기서:
- $\mu$ 는 인코더가 예측한 잠재 변수의 평균입니다.
- $\sigma$ 는 인코더가 예측한 표준편차입니다.
- $\epsilon$ 은 표준 정규 분포 $\mathcal{N}(0, I)$ 에서 샘플링된 가우시안 노이즈입니다.

이 방식으로 잠재 변수 z를 평균 $\mu$ 와 표준편차 $\sigma$ 에 의해 재매개변수화하여 샘플링합니다. 중요한 점은 이제 샘플링 과정이 미분 가능해졌다는 것입니다. 이는 $\mu$ 와 $\sigma$ 가 신경망의 파라미터로 미분 가능하기 때문에, 최적화 알고리즘에서 경사 하강법을 사용할 수 있게 됩니다.