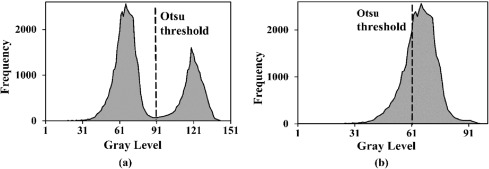
오츠 알고리즘

Otsu의 알고리즘에서 within-class variance와 between-class variance를 수식으로 간단히 표현하면 다음과 같습니다.

• within-class variance : $\sigma^2_w = w_0 \sigma^2_0 + w_1 \sigma^2_1$
• bitween-class variance : $\sigma^2_b = w_0 w_1 (\mu_0 - \mu_1)^2$

먼저 전체 이미지의 픽셀 강도에 대한 확률 분포를 고려합시다. 픽셀 강도 $i$가 나타날 확률을 $p(i)$라고 하겠습니다. 그럼 전체 이미지에 대한 확률 분포는 $\sum_{i=0}^{L-1} p(i) = 1$ (여기서 $L$은 가능한 픽셀 강도의 수)로 표현됩니다.

임계값 $t$를 기준으로 이미지를 두 클래스로 나눕니다: 클래스 1 ($C_1$, 픽셀 강도가 $t$ 이하)와 클래스 2 ($C_2$, 픽셀 강도가 $t$ 초과).

1. 클래스 확률:

• 클래스 1의 확률: $w_1(t) = \sum_{i=0}^{t} p(i)$
• 클래스 2의 확률: $w_2(t) = \sum_{i=t+1}^{L-1} p(i)$
• 여기서 $w_1(t) + w_2(t) = 1$

2. 클래스 평균:

• 클래스 1의 평균: $\mu_1(t) = \sum_{i=0}^{t} \frac{i \cdot p(i)}{w_1(t)}$
• 클래스 2의 평균: $\mu_2(t) = \sum_{i=t+1}^{L-1} \frac{i \cdot p(i)}{w_2(t)}$

3. 전체 평균:

• 전체 이미지의 평균: $\mu_T = \sum_{i=0}^{L-1} i \cdot p(i)$

Otsu's Method는 $\sigma_B^2(t)$를 최대화하는 $t$ 값을 찾습니다. 이렇게 함으로써, 두 클래스 간의 분산을 최대화하여 서로 다른 두 클래스를 명확하게 구분할 수 있는 임계값을 결정합니다.

이 수식은 "within-class variance"를 직접 계산하는 것보다 계산량이 적고, 클래스 간의 차이를 최대화하는 방식으로 최적의 임계값을 효율적으로 찾을 수 있게 해줍니다.