형태학적 연산은 이미지 처리와 분석 분야에서 이미지의 구조적 특징을 강조하거나 변형하는 데 사용되는 기법입니다. 이번 글에서는 형태학의 두 가장 기본적인 연산인 침식(Erosion)과 팽창(Dilation)의 중요한 관계, 즉 '쌍대성'에 대해 다룹니다.

🎓침식과 팽창

• 침식 : $A \ominus B$ 으로 표기하며 $B_x$(구조요소 B를 중심 $x$로 이동시킨 집합)의 모든 요소가 A에 포함된다면 해당 위치에 ${Foreground}$를 포함합니다.

  정의 : $A \ominus B = \{ x \mid B_x \subseteq A \}$

• 팽창 : $A \oplus B$ 으로 표기하며 $B_x$(구조요소 B를 중심 $x$로 이동시킨 집합)의 요소중 하나라도 A에 포함된다면 해당 위치에 ${Foreground}$를 포함합니다.

  정의 : $A \oplus B = \{ x \mid \hat{B_x} \cap A \neq \emptyset \}$

🎲침식과 팽창의 쌍대성(Duality)

침식과 팽창은 형대학적 연산의 기본적인 연산입니다. 이런 기본적인 두 연산자는 서로 선과 악처럼 Duality 관계에 있습니다.
쉽게 설명하자면, Binary Image에 대해 침식연산을 한다면 전경이 깍여나가듯이 작아지게 됩니다. 이를 배경에 대해서 설명하자만 배경이 커졌다고 할 수 있죠, 전경은 침식 되었지만, 배경은 팽창 하게 된것입니다.

수학식으로 표현하면

$(A \ominus B)^c = A^c \oplus \hat{B}$

• $A^c$는 A의 여집합(complementation)

• $\hat{B}$는 B의 반전(reflection)

  이 관계는 침식과 팽창이 서로 쌍대적인 관계에 있다는 것을 보여줍니다.
  다시 말해, 하나의 연산은 다른 연산을 통해 여집합과 관련된 관점에서 표현이 가능하다는 것을 말합니다.

---

• 침식과 팽창의 정의

  $A \ominus B = \{x \mid B_x \subseteq A \}$
  $A \oplus B = \{ x \mid \hat{B_x} \cap A \neq \emptyset \}$

• Duality 명제

  $\begin{aligned} &A^c \ominus \hat{B} = (A \oplus B)^c && \text{(1)} \\ &A^c \oplus \hat{B} = (A \ominus B)^c && \text{(2)} \\ \end{aligned}$

• 1) 증명:

  $\begin{aligned} (A \ominus B)^c & = \{x \mid B_x \subseteq A\}^c && \text{(1)} \\ &= \{ x \mid B_x \nsubseteq A^c\} && \text{(2)}\\ &= \{ x \mid B_x \cap A^c\neq0\} && \text{(3)}\\ &= \{ x \mid (\hat{B})_{-x} \cap A^c\neq0\} && \text{(4)}\\ &= A^c \oplus \hat{B} && \text{(5)}\\ \end{aligned}$

  • 설명 :
    (1) 침식의 정의 : 침식 연산은 구조 요소 $B$가 집합 $A$의 하위 집합이 되는 모든 원소 $x$의 집합을 나타낸다.
    (2) 여집합 : 침식 결과의 여집합을 사용하므로 논리적으로, 만약 $B_x$가 $A$의 하위 집합이 아니라면, 이는 $B_x$가 $A$의 여집합과 어떤 공통 원소도 가지고 있지 아니함을 의미한다.
    (3) 드모르간 법칙의 정리 : $B_x$가 $A$의 하위 집합이 아니라면, $B_x$와 $A^c$는 반드시 공통된 원소를 가지게 됨으로 교집합 기호로 이와 같이 표현이 가능하다
    (4) 구조요소의 변형 : $\hat{B}$의 정의에 따라 $\hat{B}_x = B_{-x}$이다. 그러므로 $B$를 $\hat{B}_{-x}$로 표현할 수 있다.
    (5) 팽창의 정의 : 팽창 연산의 정의를 적용하여 $A^c$와 $\hat{B}$의 팽창으로 표현이 가능하다.

• 2) 증명 :

  $\begin{aligned} (A \oplus B)^c &= \{x \mid \hat{B}_x \cap A \neq \emptyset \}^c && \text{(1)}\\ &= \{x \mid \hat{B}_x \cap A = \emptyset \} && \text{(2)}\\ &= \{x \mid \hat{B}_x \subseteq A^c\} && \text{(3)}\\ &= A^c \ominus \hat{B}&& \text{(4)}\\ \end{aligned}$

  • 설명 :
    (1) 팽창의 정의 : 팽창 연산은 구조 요소 $B$가 집합 $A$의 하위 집합이....
    (2) 여집합의 정의를 사용합니다.
    (3) 여기서, $\hat{B}_x \cap A = \emptyset$을 다르게 표현하면 $\hat{B}_x \subseteq A^c$로 표현할 수 있습니다.
    (4) 침식의 정의를 사용하여 마지막 변환을 수행합니다.

• 정리 :

  • $(A \ominus B)^c = A^c \oplus \hat{B}$
  • $(A \oplus B)^c = A^c \ominus \hat{B}$

  위 두 연산의 증명을 통해 침식 연산 후의 여집합이, 원본 이미지의 여집합을 사용하여 반전된 구조요소로 팽창 연산을 수행한 것과 동일하다는 것입니다. 이 수식을 활용한다면 계산을 더욱 효율적으로 할 수 있습니다.

---

📊예제 코드

import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import binary_erosion, binary_dilation
	# 이진영상이므로 scipy의 이진침식, 팽창을 이용함

def complement(image):                  # A^c: 이미지의 여집합
   return np.logical_not(image)

def reflect(struct_elem):               # \hat{B}: 구조 요소 반전하기
   return np.flip(struct_elem)

def translate(struct_elem, x):          # 평행 이동.
   return np.roll(struct_elem, shift=x, axis=(0,1))

def erosion(image, struct_elem):        # A \ominus B
   return binary_erosion(image, structure=struct_elem)

def dilation(image, struct_elem):       # A \oplus B
   return binary_dilation(image, structure=struct_elem)

def plot_image(image, title):
   plt.imshow(image, cmap='gray')
   plt.title(title)

A = np.array(
   [
       [0,0,0,0,0,0,0,0,0,0],
       [0,1,1,1,0,0,1,1,1,0],
       [0,1,1,1,0,1,0,1,1,0],
       [0,0,1,0,0,0,0,1,0,0],
       [0,0,0,0,1,0,0,0,0,0],
       [0,0,0,1,1,1,0,0,0,0],
       [0,0,0,1,1,1,1,1,0,0],
       [0,0,0,1,1,1,1,0,0,0],
       [0,0,0,0,0,0,0,1,0,0],
       [0,0,0,0,0,0,1,1,1,1]
   ], 
   dtype=bool)
B = np.array([[0,0,0], [0,1,1], [0,1,0]], dtype=bool)

A_oplus_B = dilation(A, B)
A_ominus_B = erosion(A, B)

plt.subplot(2,2,1)
plot_image(A, "A")

plt.subplot(2,2,2)
plot_image(B, "B")

plt.subplot(2,2,3)
plot_image(A_oplus_B, "A_oplus_B")

plt.subplot(2,2,4)
plot_image(A_ominus_B, "A_ominus_B")

plt.tight_layout()
plt.show()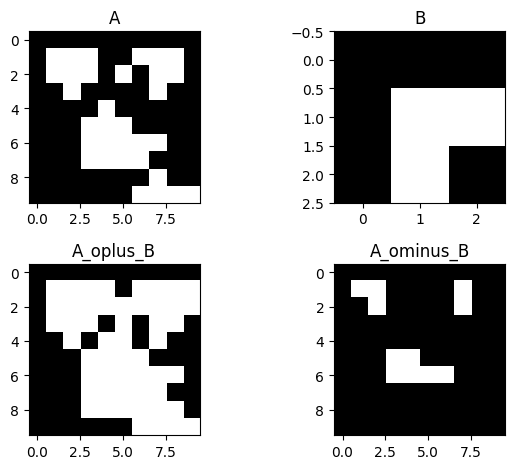

• 연산과정 증명 부는 나중에