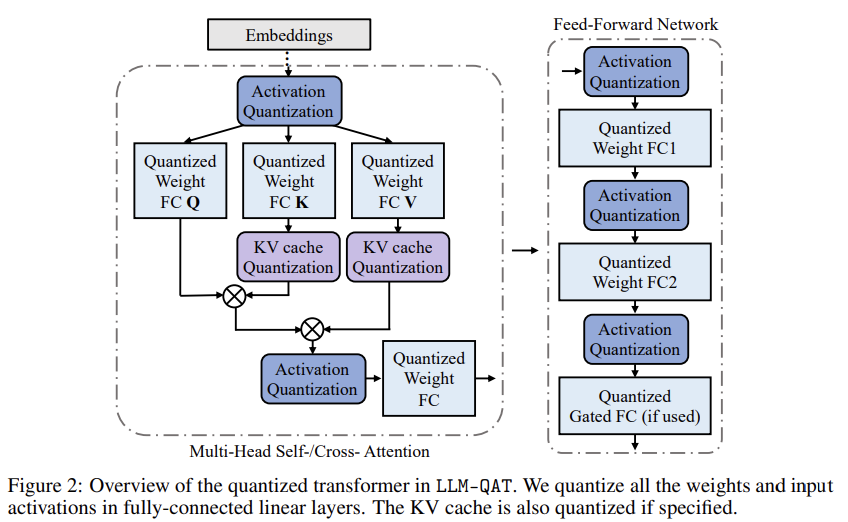
LLM-QAT: Data-Free Quantization Aware Training for Large Language Models

---

LLM-QAT에 대한 내용

Abstract

여러 PTQ(Post-Training Quantization) 기법이 LLM에 적용되어, 8 bit까지 우수한 성능을 보였다. 그러나 이러한 기법은 더 낮은 bit 정밀도에서 한계를 보인다.
==> LLM에 대해 Quantization Aware Training(LLM-QAT)을 적용하여 quantization level을 더욱 향상시키고자 한다.

이를 위해 pre-trained된 model이 생성하는 결과물을 활용하는 data-free distillation을 제안
==> original output 분포를 더 잘 보존 + PTQ와 유사하게 training data와 무관하게 모든 generative model을 quantizing할 수 있음

// original output 분포를 더 잘 보존
// ==> 기존 pre-trained된 model이 생성하는 output 분포를 더 잘 따라간다는 말
// ==> 성능이 크게 저하 X

Weight와 actiation 뿐만 아니라, KV cache도 quantizing한다.

---

1. Introduction

LLM에서 parameter수 ↑(model 크기 ↑)
==> 성능 ↑
==> 수십억, 수백억 개의 parameter를 가진 LLM 탄생

But 이러면 너무 무거워짐

==> weight, activation에 대한 8-bit quantization

But 650억 개의 parameter를 가진 LLaMA model에서 여전히 65GB의 GPU 메모리를 차지
+
attention layer의 activation를 저장하는 Key-Value cache는 수십 GB차지

==> KV cache도 quantizing
==> 긴 sequence 생성을 위한 throughput bottleneck을 완화하는 데 성공

data-free distillation이 필요한 이유

1. LLM training은 기술적으로 어렵고 resource를 많이 소모
2. QAT에는 training data가 필요한데, LLM의 경우 이러한 데이터를 확보하는 것이 어렵다

data-free distillation 장점

1. 원래의 training data의 available에 상관없이 모든 genarative model에 적용할 수 있다
2. 원래 모델의 output distribution을 더 잘 보존 (이는 원래 training data의 큰 부분 집합을 사용한 training과 비교해서도 우수하다)

   Q1. 근데 그럼 바보 모델이 생성한 training data로 학습하게 되면 더 바보가 되는 거 아님? 즉 일반화 성능이 떨어지는 거 아님?
   A1.
   아니지, pre-trained된 model은 똑똑한 model이라고 생각하는게 맞지

---

2. Method

LLM을 QAT하는데 2가지 어려움

1. LLM은 zero-shot generalization에서 우수한 성능을 발휘하도록 pre-trained되었으며, quantized 후에도 이러한 능력을 유지하는 것이 중요
   ==> 2.1. Data-free Distillation
2. LLM은 소형 model과는 다른 독특한 weight와 activation distribution을 나타내며, 이는 outlier가 다수 존재한다는 특징을 가진다.
   ==> 2.2. Quantization-Aware Training

   Q2. zero-shot generalization은 무엇이고, LLM에서 이것이 중요한 이유는?
   A2.
   

2.1. Data-free Distillation

pre-training data의 distribution을 제한된 양의 fine-tuning data로 가깝게 synthesize하기 위해, pre-trained된 model을 활용하여 next token data generation을 제안.

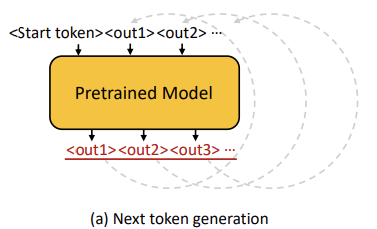
data 생성 과정에서 3가지 sampling 전략들

1. Top-1 sampling : 가장 확률이 높은 token을 다음 token으로 선택하는 단순한 방식
   단점 : 생성된 문장이 다양성이 부족하고, 몇몇 token이 주기적으로 반복되는 문제 有
2. stochastically sampling : 사전 학습된 모델의 SoftMax 출력을 확률로 사용하여 분포에서 다음 토큰을 확률적으로 sampling하는 방법
3. Hybrid Sampling : 첫 3~5개의 token은 deterministically하게 Top-1 sampling(높은 신뢰도를 위해). 이후 token은 stochastically sampling(다양성을 위해). (∵ 초기 몇 개의 token이 prediction trend를 결정하는 데 중요한 역할)

---

2.2. Quantization-Aware Training

2.2.1. Preliminaries

Linear Quantzation은 실수를 clipping 않하는 지 하는 지에 따라 MinMax quant, Clipping-based quant로 나뉜다.

---

MinMax Quantization

MinMax Quant는 모든 값 범위를 유지한다.
$\mathbf{X}_Q^i = \alpha \hat{\mathbf{X}}_Q^i = \alpha \left[ \frac{\mathbf{X}_R^i - \beta}{\alpha} \right] + \beta$
$식 (1)$

$X^Q$ : quantized 된 변수
$X_R$ : fp 변수
$i$ : tensor의 $i$번째 요소
$\alpha$ : scaling factor
$\beta$ : zero-point value

Symmetric Quantization의 경우,
$\alpha = \frac{max(|X_R|)}{2^{N-1}-1}, \beta = 0$

Astmmetric Quantization의 경우,
$\alpha = \frac{max(X^R)-min(X^R)}{2^N-1}, \beta = min(X^R)$

---

Clipping-based Quantization

outlier를 clipping하면 precision을 개선하고, 중간 값에 더 많은 비트를 할당할 수 있다.
$\mathbf{X}_Q^i = \alpha \hat{\mathbf{X}}_Q^i = \alpha \left[ \text{Clip}\left( \frac{\mathbf{X}_R^i - \beta}{\alpha}, 0, 1 \right) \right] + \beta.$
$식(2)$

---

2.2.2. Quantization for Large Language Models

Quantization function

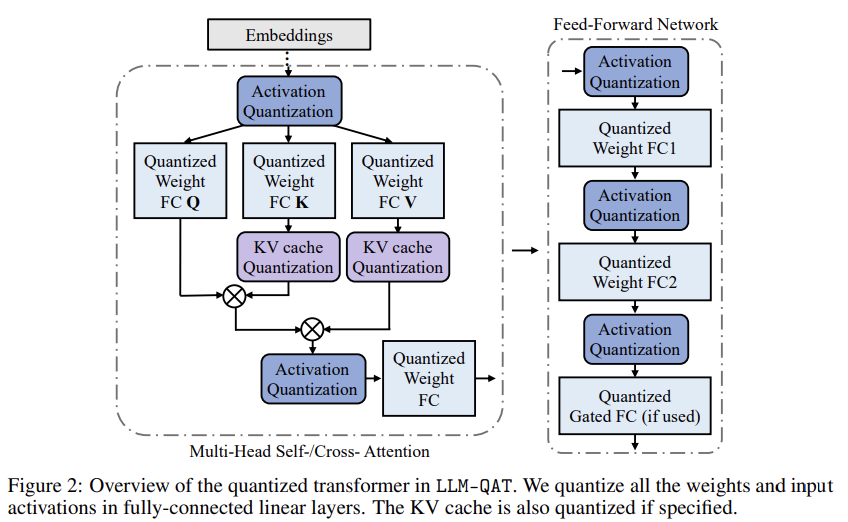
outlier 문제점
quantization step size를 증가시켜, 중간 값(실제로 양자화 범위 내에서 대부분의 데이터가 위치하는 값)의 precision을 저하시킨다.

==> 그럼 outlier를 없애면?
==> outlier clipping은 LLM 성능에 부정적이다. 특히 training 초기 단계에서 clipping은 매우 높은 perpelxity score를 초래하여, 이후 fine-tuning으로도 회복 X

==> outlier clipping 없이 quantization

GLU(Gated Linear Unit)기반 model에서 weight와 activation이 대체로 symmetric 하게 분포
==>
Symmetric MinMax Quantization

Symmetric MinMax Quantization 식은 위 식(1),(2)를 기반으로 아래와 같음을 알 수 있다.

$\mathbf{X}_Q^i = \alpha \left[ \frac{\mathbf{X}_R^i}{\alpha} \right], \quad \alpha = \frac{\max(|\mathbf{X}_R|)}{2^{N-1} - 1}$
$식(3)$

Quantization granularity level은
activation에서는 per-token,
weight에서는 per-channel로
Quantization한다.
즉, 아래 Figure 3의 (a)이다.

---

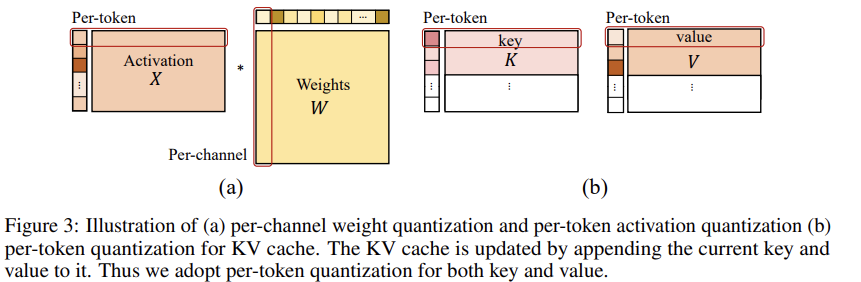
Quantization-aware training for key-value cache

LLM에서 weight, activation 말고도 KV Cache는 상당한 양의 메모리를 소비한다.

But

기존 연구들은 주로 PTQ에 초점을 맞췄으며, 이에 대한 연구는 제한적이었다.

==> KV Cache에 QAT 적용

Figure 3 (b)에서 볼 수 있듯, K,V는 per-token으로 생성되므로, 식(3)의 per-token quantization을 채택했다.

---

Knowledge distillation

Cross-Entropy Based Logits Distillation을 사용하여, full precision으로 pre-trained된 선생 네트워크로부터 quantized된 학생 네트워크를 훈련한다.

$\mathcal{L}_{CE} = -\frac{1}{n} \sum_c \sum_{i=1}^n p_c^T(X_i) \log\left(p_c^S(X_i)\right),$

$i$ : 현재 batch에서 i번째 sample (n : 총 문장 수)
$c$ : 클래수 수 (본 연구에서는 vocabulary 크기와 동일)
$T, S$ : 선생, 학생 네트워크
$p^T_c(X_i)$ : 선생 네트워크의 c번째 클래스에 대한 예측 확률

---

3. Experiments

생략

---

4. Related Works

생략

---

5. Conclusion and Limitations

생략

---