
Abstract
Implicit feedback(클릭, 구매)를 이용해 아이템을 추천하는 방법론은 (MF, KNN) 등 다양
그러나 다음과 같은 방법으로는 Rank를 최적화할 수 없음
이에 따라 Ranking 방법론으로 BPR-OPT를 제시하고자 함
이는 베이지안 방법론을 사용한 사후 확률 추정기이며 부트스트랩과 SGD를 이용해 MF, K-nn에 적용할 수 있음
Introduction
아이템 추천 Task는 유저별 아이템 집합 랭킹을 만드는 것
아이템에 대한 유저의 선호도는 유저의 과거 Interation를 통해 예측 가능
본 논문을 통해 Implicit feedback으로 아이템 집합 랭킹을 만들고자 함
Contribution
- Bayesian 추론 기반 optimization 기법 제시 후, 이 기법이 AUC를 극대화 하는 문제와 동치임을 보임
- BPR-OPT를 최대화 하기 위한 알고리즘(Learn BPR)을 제안
- Learn BPR을 MK, kNN에 적용
- BPR-Opt가 다른 optimization 기법보다 우수함을 보임
관련 연구
기존 implicit data의 design matrix는 binary로, user가 item을 클릭할 확률을 예측하는 task (Least-Sqaure 사용)
본 논문에서 주장하는 rangking optimization은 이와 달리, 두 item 쌍의 선호 강도를 반영한 hyperparameter optimizaiton
Personalized Ranking
Implicit feedback은 Positive 관측만이 사용 가능
관찰되지 않은 유저-아이템 pair는 Negative일지, unknown일지 알 수 없음
Formula
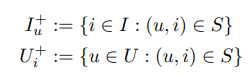
U X I의 Implicit feedback matrix는 구매, 조회, 클릭 모두 사용 가능
모든 아이템의 개인 맞춤형 종합 랭킹을 제공하는 것이 목표
Analysis of the problem setting
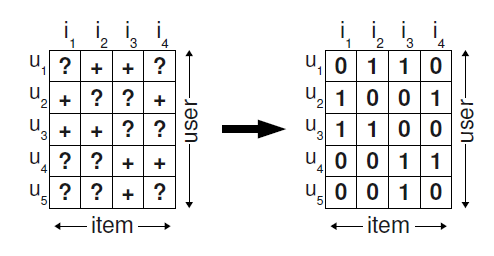
Implicit data는 positive class만 관측됨으로, 남아있는 데이터는 negative와 unknown의 결과물
흔히 머신러닝 task에서는 +를 1로, negative와 unknown을 0으로 labeling 한 뒤, 이를 예측하기 위해 학습
이는 unknown도 negative로 설정하는 것으로서, 실제 user가 구매할지도 모르는 item을 무시하는 효과가 나옴
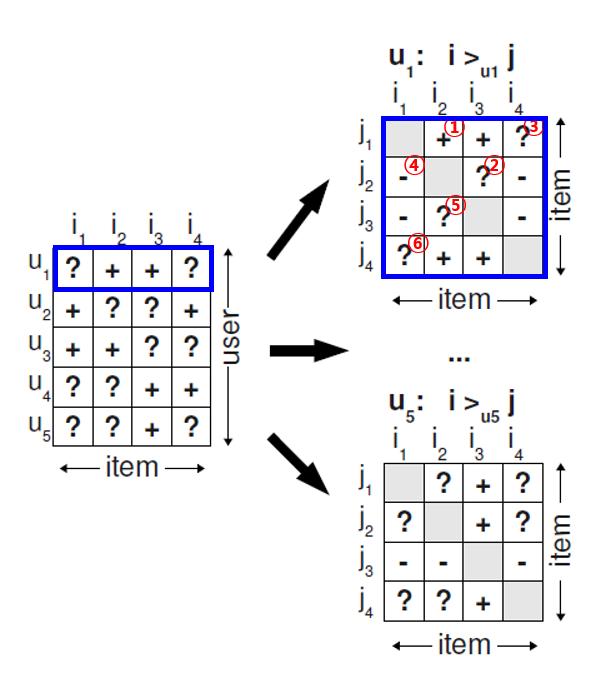
저자는 다음과 같은 가정의 desing matrix로 문제를 해결
- user는 관측된 item을 관측되지 않은 모든 item보다 선호
- 관측된 item 중에서는 선호 강도를 추론할 수 없음
- 관측되지 않은 item 중에서도 선호 강도를 추론할 수 없음
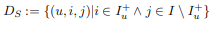
이를 formula 하기 위해, 데이터 셋을 다음과 같이 명시
이와 같이 ranking 기반으로 문제를 정의하면 다음과 같은 특징을 가짐
- 관측되지 않은 item에도 정보를 부여해 간접적으로 학습할 수 있음
- 관측되지 않은 item들에 대해서도 ranking이 가능해짐
Bayesian Personalized Ranking (BPR)
BPR Optimization Criterion
위에서 정의한 Ds를 바탕으로 Bayesian Optimization, 즉 Maximum A posteriori Estimation을 진행
사전확률을 이용한 MLE를 찾는 것으로 다음과 같은 가정 하에서 진행됨
- 모든 유저들은 서로 독립
- 특정 유저의 아이템 pair 순서가 다른 모든 pair 순서와 독립
이 떄 >u에 대한 확률 분포를 예측하는 것으로, 이는 베르누이 분포를 따름

다만 여기에서, 개인 rank를 얻는 것은 보장되지 않음
따라서 MF와 kNN 등 item 사이의 관계를 포착하는 모델을 적용

x^uij가 MF, kNN 등의 user와 item i, j의 함수이며
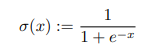
시그마는 로지스틱 시그모이드 함수
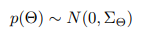
이후 사전확률 분포는 다음과 같은 정규 분포를 따른다고 가정하며, Hyperparmeter 개수를 줄이기 위해 공분산행렬은 대각행렬로 가정
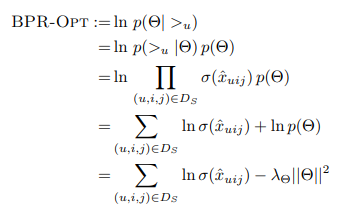
따라서 최종 BPR-OPT는 다음과 같이 formula 됨
lambda theta L2 norm은 regularization parameter
BPR Learning Algorithm
하이퍼파라미터 Theta를 update하는 방법으로는 stochastic graiden descent 방법을 사용
- 일반적으로 관측된 i 집단이 j 집단보다 개수가 작음
- 따라서 booststrap sampling을 통해 u,i,j를 randomg하게 선택한 stochastic gradient descent 방법은 dataset의 비대칭성을 어느정도 해소할 수 있음
Conclusion
BPR-OPT는 베이지안 방법론을 이용한 최대 사후 확률 추정기로서, 이를 적용한 모델이 기존 모델에 비해 좋은 성능을 보여주는 것을 확인할 수 있음
