Loss Function

• 모델의 성능을 측정하는 척도를 지정하기 위해 사용

• Error를 낮추는게 학습의 목표 -> Error에 대해 정의하는 것이 중요

Error = Variance + Bias

Variance: 추정값의 평균과 추정 값 들 간의 차이

Bias: 추정 값의 평균과 참 값 들 간의 차이

$Error = \sum (\hat{y} - y)^2$

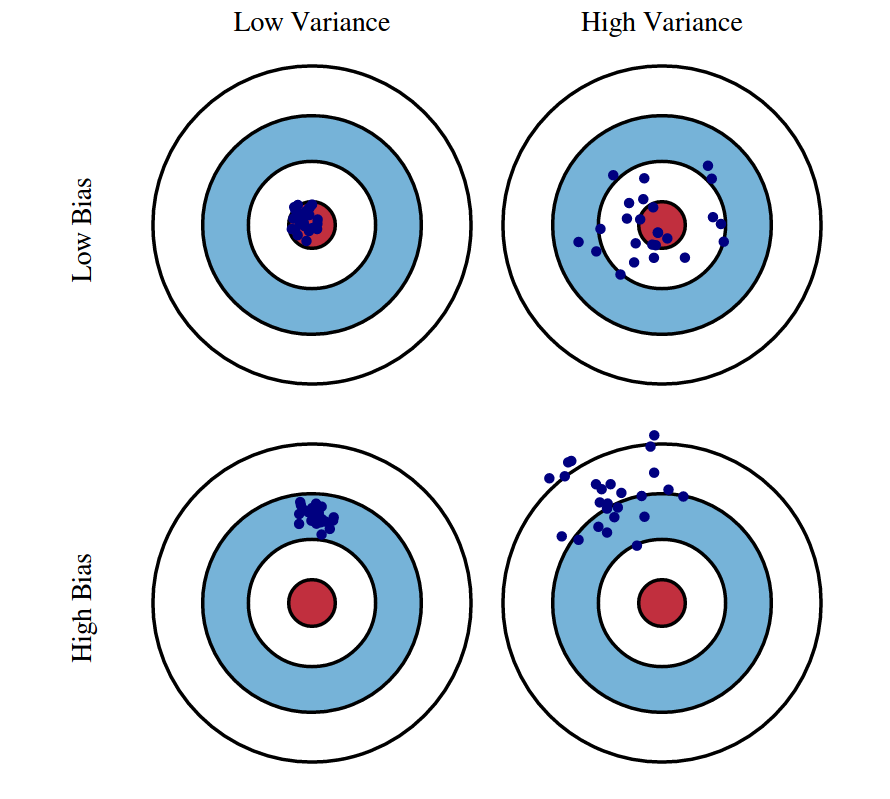
Lecture 12: Bias-Variance Tradeoff

$Error = Noise(Data) + Variance + Bias$

$EX)\quad Simple\,Linear\,Regression$

$E(y_i) = \beta_0 + \beta_1x_i^1+\beta_2x_i^2$

Dependent Variable(추정값) = Constant(상수) + Coefficient(계수)

왜 제곱을 사용할까?

• 추정값과 참 값의 차이를 표현하는 방식의 차이
  하지만 제곱의 장점은 빠르게 문제 해결이 가능함
• Closed Form : 제곱을 사용하는 LossFunction
  미분 불가능(MAE)과 미분 가능(MSE,RMSE)

$\beta$(계수) 추정법

simple & Multi-Linear Regression

• 각 $\beta$에 대한 편미분을 사용하여 추정을 수행함
• $\beta$가 여러 개 일때 똑같이 각 $\beta$에 대해 미분 수행 후 추정함

추정한 $\beta$에 대한 검증

• 귀무가설 vs 대립가설

• $\beta$에 대한 p-value가 낮으면 기울기가 0이 아닌 것으로 판명

• 통상적으로 p-value가 0.05이하면 의미 있다고 판단

• 즉, p-value가 0.05 이하면 $H_0$(귀무가설)은 기각되며 $H_1$이 채택 됨

X의 Feature에서 중요한 변수를 Ranking

• P-value가 0.05인지 확인
• 스케일링이 되어 있고, 유의미한 변수라면 $\beta$(계수)가 클수록 중요

모델 평가 및 지표

$R^2$

• 평균으로 예측한 것에 대비 분산을 얼마나 축소 시켰는지에 대한 판단
• SSR : 회귀식에 의해 설명되지 않는 편차(Residual Sum of Squares)
• SSE : 회귀식에 의해 설명되는 편차(Explained Sum of Squares)
• SST = SSR + SSE : 총편차(Total Sum of Squares)

현업에서는 0.25의 $R^2$만 되도 유의미하다고 판단. 현업에서는 0.3이상인 경우도 찾기 힘듦

Feature Selection

Overfitting을 방지하기 위한 Feature Selection

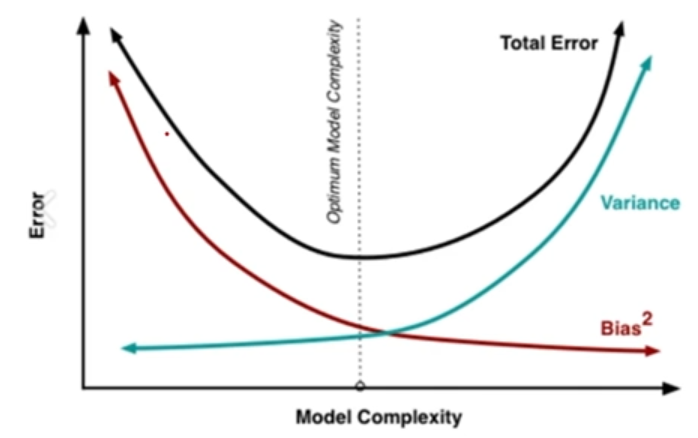
Feature의 수가 많아질 수 록 Model Complexity(복잡도)는 높아짐
Model Complexity가 높아지면 Bias는 낮아지는 반면 Variance가 높아짐
Bias와 Variance의 Trafe-off 최적점을 도출해야 함

Exhaustive Search(완전 탐색)

• Feature의 최적 조합을 찾아냄
• 변수가 많아질 수록 시간이 너무 오래 걸리는 단점

Forward Selection

• Variable을 하나씩 Sequentially 추가

Backward Elimination

• 뒤에서 부터 제거

Stepwise Selection

• Forward Selection과 Backward Elimination을 번갈아 가며 수행함
• 시간은 오래걸리지만 최적의 Variable Subset을 찾을 가능성이 높음

기존 Feature Selection 단점

• 전통적인 Feature Selection 방법은 Variables 가 커짐에 따라 시간이 매우 오래 걸리게 됨
• 최적의 Variables Subsets을 찾기 어려움
• 가성비가 떨어짐

Model이 Error를 Minimize하는 과정에서 Feature를 Selection 해줄 수 있는 방법은 없을까?

Penalty Term

• 불필요한 Feature에게 '벌'을 부여해서 학습하지 못하게 함
• Error를 Minimize하는 제약 조건에서 필요 없는 Feature의 $\beta$에 Penalty를 부여함