Ridge Regression

• $\beta^2$에 Penalty Term을 부여하는 방식

• Penalty Term을 추가한 Regularized Model 의 경우 Feature간 Scaling이 필수

  $L(\beta) = \min_{\beta} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^{p} \beta_j^2$

• $L_2 -norm= L_2 Regularization$

• MSE Contour 중심에서 멀어질수록 Error 증가 -> Train Error를 조금 증가시키는 과정 (Overfitting 방지)

• Ridge Estimator 와 MSE Contour가 만나는 점이 제약 조건을 만족하면 Error가 최소가 됨

Lasso Regression

• $|\beta|$ = $L_1 - norm = L_1 Regularization$에 Penalty Term을 부여하는 방식

Gradient Descent (경사하강법)

: 최적해를 보장하진 않지만 복잡한 여러 해가 존재할 때 가장 유용한 방법

• Local Minima에 빠질 수 있음 -> Momentum을 준다.
• Global Minimum이 있는지 알 수 없음

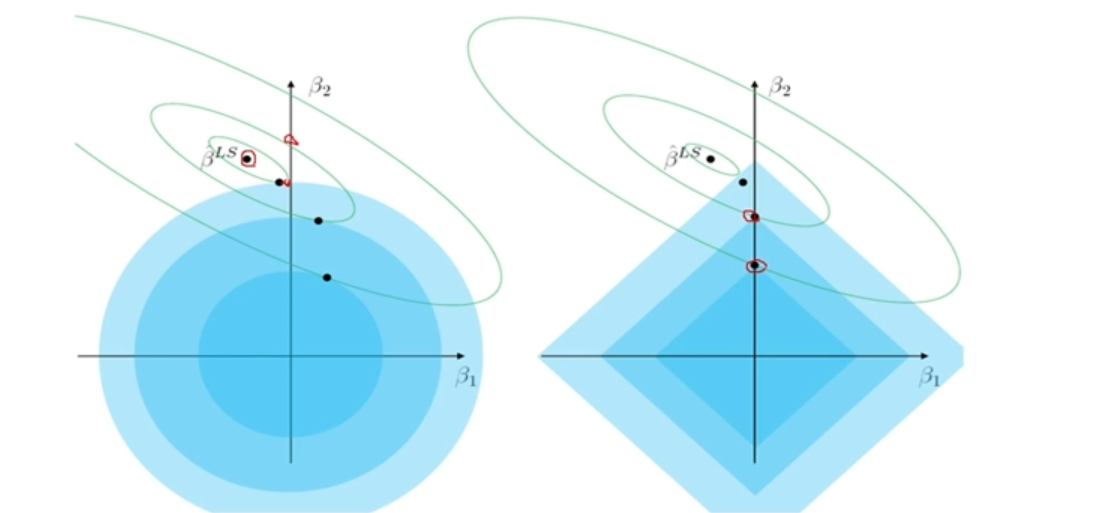
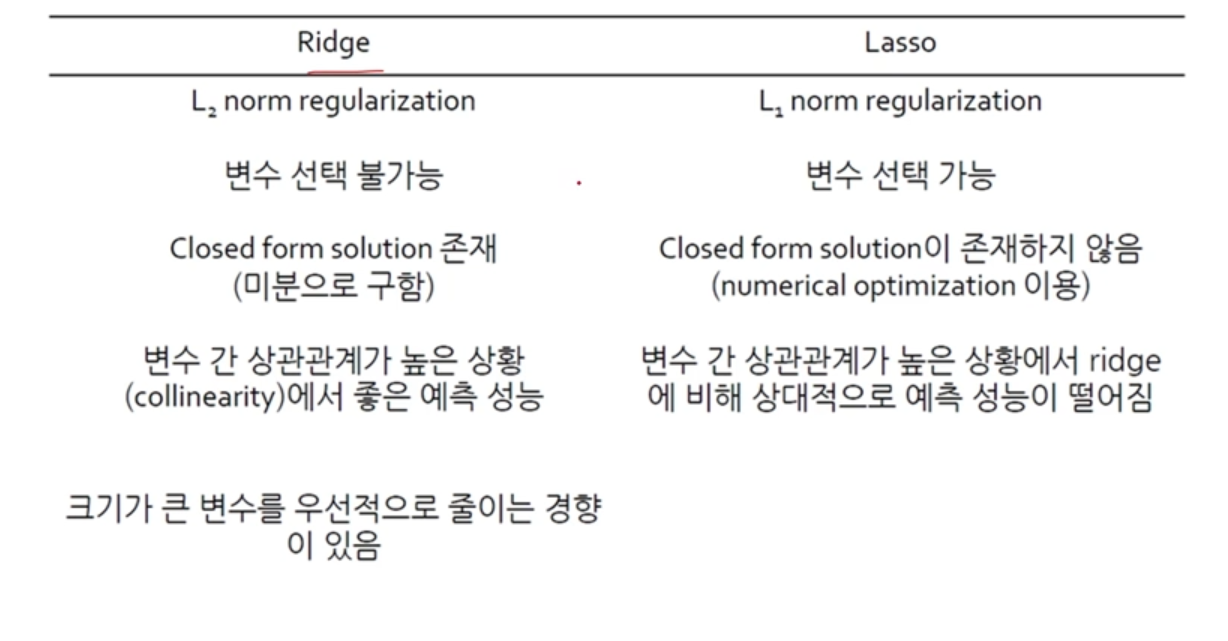
Ridge vs Lasso

• 패널티 $\lambda$가 커짐에 따라 모든 계수의 크기가 감소
• Ridge는 크기가 큰 변수가 더 빠르게 감소
• Lasso는 예측에 중요하지 않은 변수가 더 빠르게 감소
  

ElasticNet

• Ridge의 L1-norm과 Lasso의 L2-norm을 섞어 놓았음
• 상관관계 높은 변수들 동시에 선택
• 인접한 변수들 동시에 선택
• 사용자가 정의한 그룹 단위로 변수 선택
  

그외 회귀모델

Prior Knowledge	Regularization Method
상관관계 높은 변수들 동시에 선택	Elastic Net
인접한 변수들 동시에 선택	Fused Lasso
사용자가 정의한 그룹 단위로 변수 선택	Group Lasso
사용자가 정의한 그래프의 연결관계에 따라 변수 선택	Grace