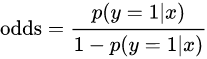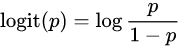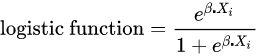1. 로지스틱 회귀란?

로지스틱 회귀는 영국의 통계학자인 D.R.Cox가 1958년에 제안한 확률 모델로서, 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용되는 통계 기법이다.

로지스틱 회귀의 목적은 일반적인 회귀 분석의 목표와 동일하게 종속 변수와 독립 변수간의 관계를 구체적인 함수로 나타내어 향후 예측 모델에 사용하는 것인데, 이는 선형 회귀 분석과 유사하다.

하지만, 로지스틱 회귀는 선형 회귀 분석과는 다르게 종속 변수가 범주형 데이터를 대상으로 하며, 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 분류 기법으로도 볼 수 있다.

종속 변수의 범주의 갯수에 따라 이항 로지스틱 회귀나 다항 로지스틱 회귀로 구분되고, 이항 로지스틱 회귀의 경우에는 종속변수의 결과가 범위 [0,1]로 제한되고, 조건부 확률 P(y|x)의 분포가 정규분포 대신 이항분포를 따른다.

따라서, 단순 선형 회귀를 적용하면 안되고 연속적이고 증가함수이며, 종속 변수의 범위가 [0,1]인 값을 갖는 연결함수가 제안되었다. 그중에서 대표적으로 로지스틱 모형과 검벨 모형이 있는데, 이 중에서 계산상의 편의를 위해 로지스틱 모형이 주로 사용된다.

2. 로지스틱 함수

먼저, 성공 확률이 실패 확률에 비해 몇 배 더 높은가를 나타내는 odds를 계산한다. 그 식은 아래와 같다.

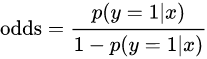
로짓 변환은 오즈에 로그를 취한 함수로서 입력 값의 범위가 [0,1] 일 때 출력 값의 범위를 [-$\infty$,$\infty$]로 조정한다.

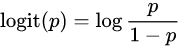
마지막으로 로지스틱 함수는 로짓 변환을 통해서 만들어진다. 이는 독립 변수 x가 주어졌을 때, 종속 변수가 1의 범주에 속할 확률을 의미한다. 이는 곧 p(y=1|x)를 의미한다. 그 수식은 다음과 같다.

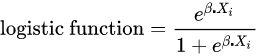
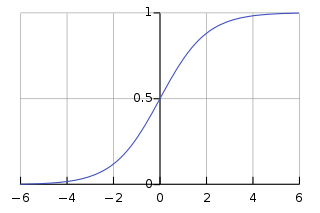
로지스틱 함수를 그래프로 표현하면 다음과 같고, 모든 입력 값에 대해서 종속 변수는 [0,1]의 범위를 갖는다. 그리고 이 함수는 결국 우리가 흔히 알고있는 Sigmoid 함수를 의미한다. 예를 들면, 이진 분류가 필요한 상황에서 Sigmoid 활성화 함수를 출력층에 사용하게 되면, Sigmoid 함수는 종속 변수(Output)가 1의 범주에 속할 확률을 뜻하므로 특정 클래스(이진 분류 대상)일 확률을 의미하게 된다.