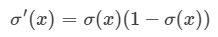1. 활성화 함수를 사용하는 이유?
활성화 함수는 신경망 구조에서 입력값에 대해서 가중치를 곱한 뒤에 적용하는 비선형 함수를 의미한다.
세상에 존재하는 많은 문제는 대부분 비선형이기 때문에 선형 함수로 해결할 수 없는 경우가 많다. 이처럼 활성화 함수를 사용하는 이유는 신경망 구조에서 비선형성을 추가하여 아래와 같이 XOR과 같은 비선형 문제들을 해결하기 위해서 이다.
이는 앞에서 포스팅한 퍼셉트론에서 다층 퍼셉트론이 은닉층을 사용하는 이유와 같은 맥락이다.
2. 퍼셉트론에서 사용된 활성화 함수?
그렇다면 퍼셉트론에서는 어떤 활성화 함수를 사용했을까?
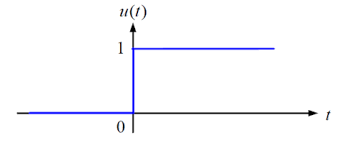
퍼셉트론에서 사용된 계단 함수(Step Function)는 가장 기본이 되는 함수로써, 그래프 모양이 계단과 유사하다. 함수 식은 다음과 같다.
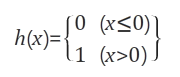
3. Sigmoid
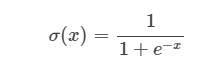
위의 수식은 Sigmoid 함수를 의미하며, Logistic 함수라고도 불리고 신경망에서 종종 이용하는 활성화 함수이다. 먼저, Sigmoid 함수가 사용된 계기에 대해서 이해하기 위해 지난 포스팅에서 로지스틱 회귀 개념을 잠시 짚고 넘어가는 것을 추천한다.
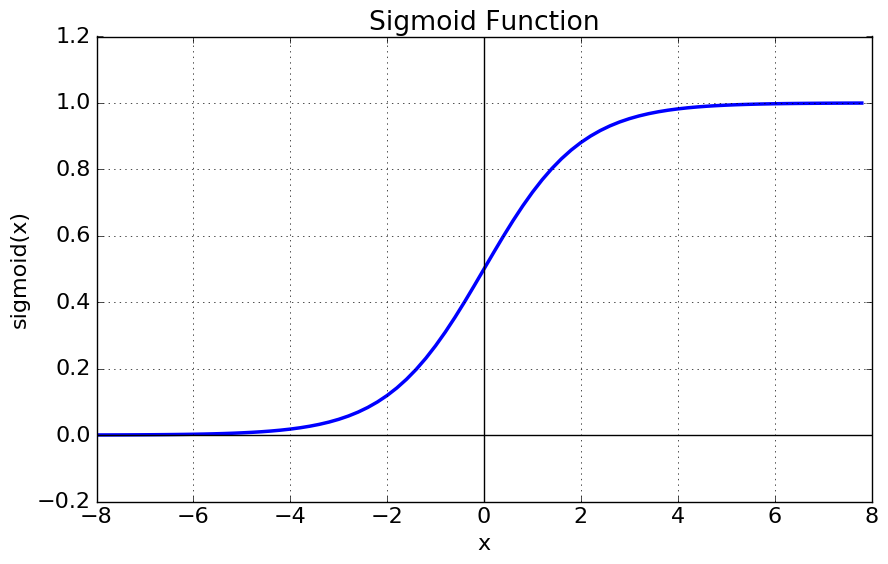
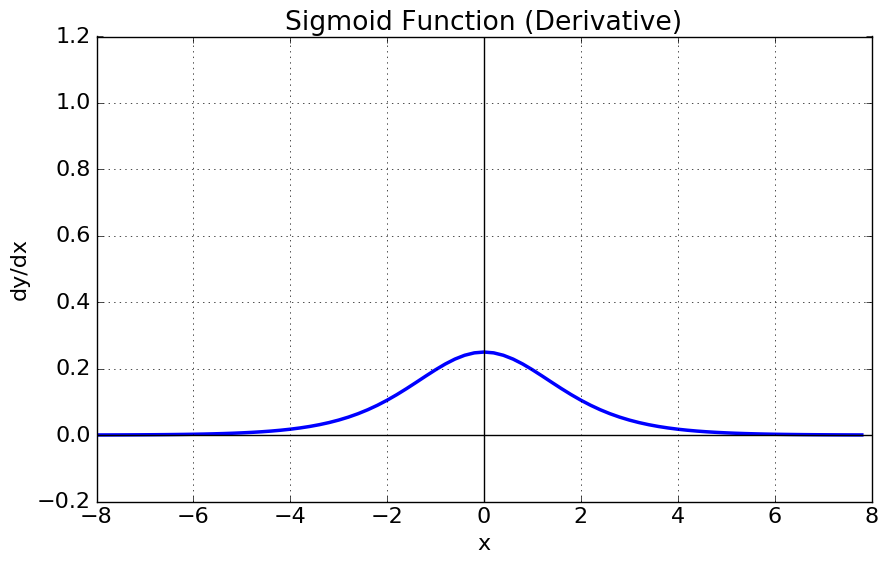
Siomoid 함수와 미분에 관한 그래프는 위와 같다. 그래프에서 보는 것과 같이 Sigmoid 함수는 [0, 1]의 범위의 출력 값을 가지기 때문에 이진 분류에 잘 사용되고 기울기가 범위가 [0, 0.25]이므로 Gradient Exploding 현상을 억제하는 효과를 가진다. 하지만, 다음과 같은 문제점을 포함하고 있다.
1. Gradient Vanishing 현상
1) Not Zero-Centered
Sigmoid 함수는 [0, 1]범위의 양수를 출력하고, 평균이 0이 아닌 0.5이므로 편향 이동이 발생한다. 여기서 편향 이동이란, 출력의 가중치 값이 입력의 가중치 값보다 커지는 현상을 의미한다. 이는 곧, 각 Layer를 거치면서 분산이 거치게 되면서 활성화 함수의 출력이 0 또는 1로 수렴될 확률이 높아진다.
2) Gradient Sturation
입력 값이 일정이상 올라가게 되거나 내려가게 되면 미분 값이 거의 0에 수렴하게 되어 Backpropagation시에 미분값이 소실될 가능성이 크다.
2. 학습 속도 저하(Zig Zag 현상)
Sigmoid 함수은 [0, 1] 범위의 양수를 출력하고, 미분 또한 항상 양수 값을 가진다. 이에 따라 모든 가중치는 같은 방향으로 학습하게 되어 학습 속도에 저하가 발생하게 된다. 이에 대한 증명은 다음과 같다.

유의 사항
Sigmoid 함수는 일반적으로 Gradient Exploding을 억제할 수 있는 효과를 가지지만, 모델 학습시에 초기화 된 가중치가 매우 큰 경우에는 Gradient Exploding 현상이 발생할 수 있다.

4. Tanh
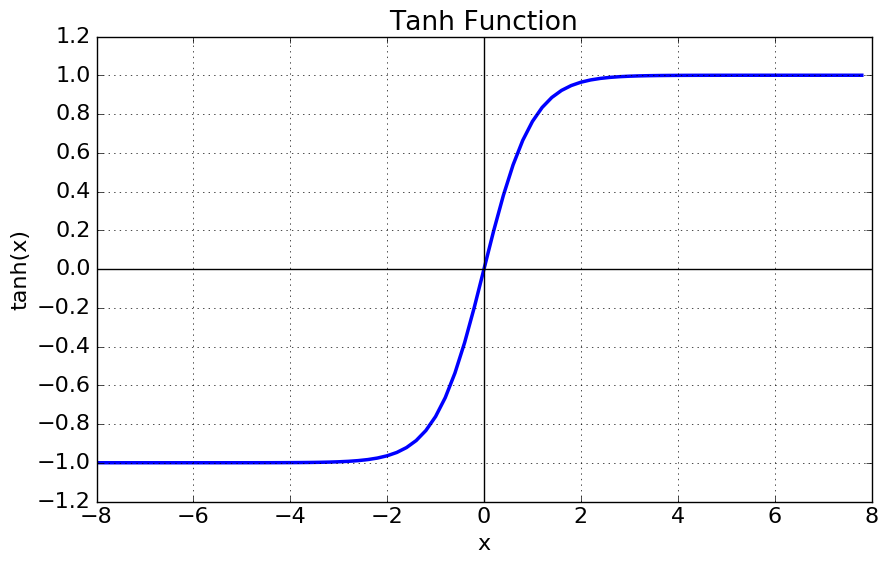
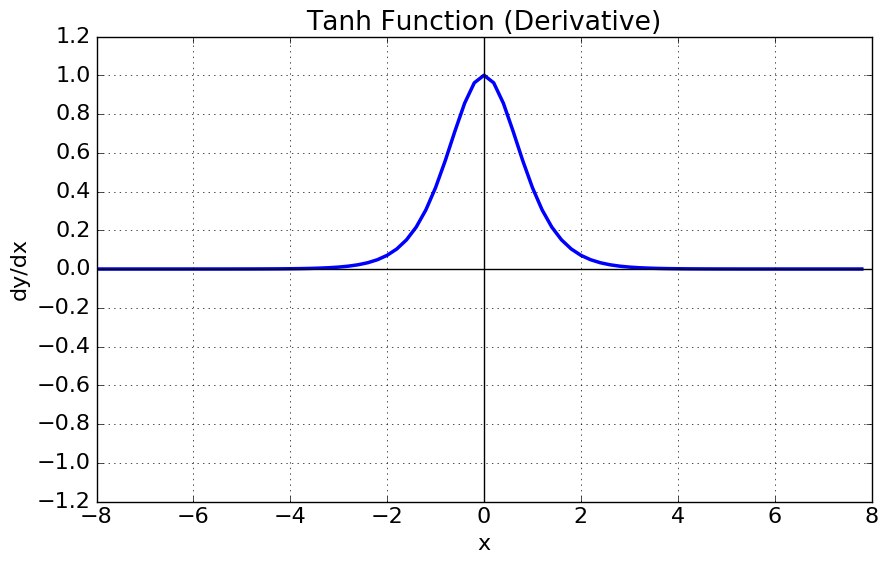
Tanh 함수는 쌍곡선 함수중 하나로써, Sigmoid 함수를 변환하여 얻을 수 있다. 식은 다음과 같다.
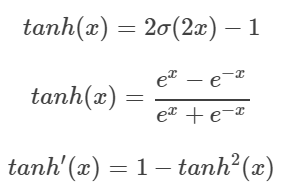
Tanh 함수는 [-1, 1]의 범위의 출력을 가지고, 평균 값을 0으로 하기 때문에 편향 이동 문제나 Zig Zag 현상을 해결 할 수 있다. 하지만, 미분 그래프는 여전히 일정한 값 이상 혹은 이하인 경우 Gradient 값이 0으로 수렴하기 때문에 Gradient Vanishing 문제는 유효하다.
5. Softmax
Softmax는 Multi Classification Task에서 출력층에서 주로 활용되는 활성화 함수이다. 출력층의 각 노드의 값을 [0, 1] 범위의 확률 값으로 표현하고, 전체 노드 출력의 합은 1이다. 식은 다음과 같다.
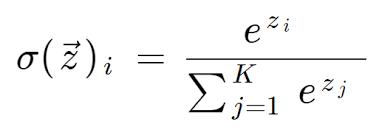
다음 포스팅에선 Sigmoid와 tanh에서 공통적으로 발생하는 문제인 Gradient Vanishing 문제를 ReLU로 어떻게 해결했는지에 대해 다뤄보고자 한다.