[N412] TIL 및 회고

Sea Panda·2023년 1월 11일

코드스테이츠

부트캠프 TIL

목록 보기

36/46

0. 학습목표

Level 1.

신경망이 학습되는 메커니즘(순전파, 손실계산, 역전파)에 대해 적절한 비유를 들어 설명할 수 있다.
경사 하강법(Gradient Descent, GD)을 통해 갱신되는 과정을 대략적으로 설명할 수 있다.
옵티마이저(Optimizer)의 개념과 확률적 경사 하강법(Stochastic Gradient Descent, SGD) 및 미니 배치 경사 하강법(Mini-Batch Gradient Descent)의 개념에 대해 설명할 수 있다.

Level 2.

편미분(Partial Derivatives)과 연쇄 법칙(Chain Rule)에 대해 이해하고 곱셉 노드, 덧셈 노드 및 활성화 함수에 대한 미분 예제를 풀 수 있다.
편미분과 연쇄법칙을 사용하여 역전파 과정을 설명할 수 있다.

Level 3.

이론적으로 이해한 내용을 파이썬 코드로 구현할 수 있다.
구현한 함수를 모두 엮어 신경망 학습을 파이썬 코드로 작성할 수 있다.

1. 신경망 학습(Training Neural Network)

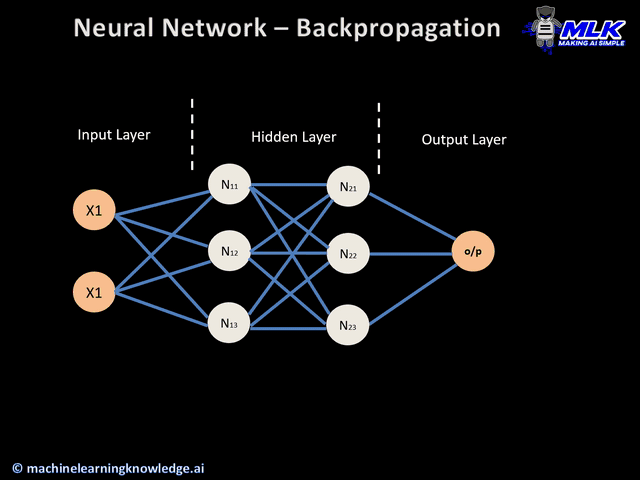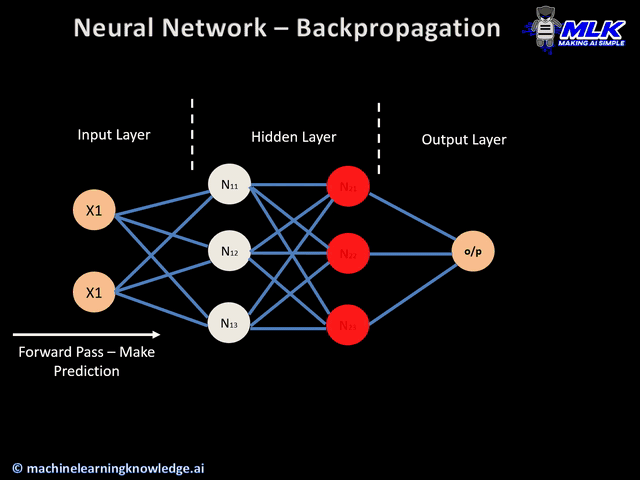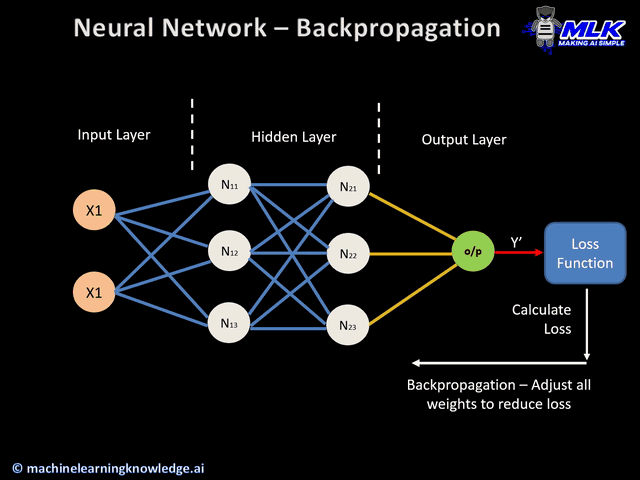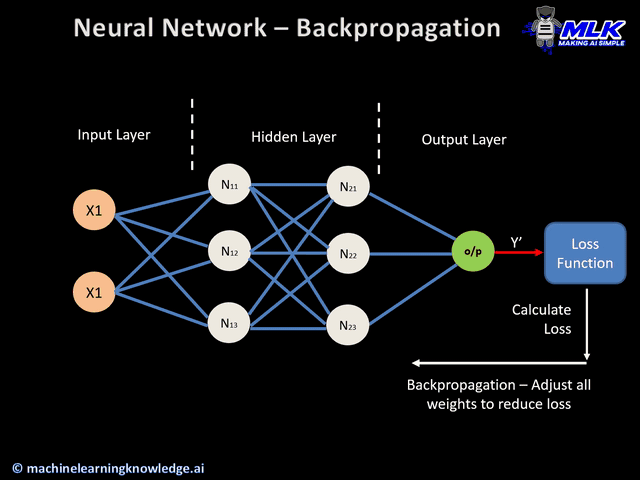
신경망은 기본적으로 위의 gif파일처럼 학습된다.
1. 데이터가 입력되면 신경망 각 층에서 가중치 및 활성화 함수 연산을 반복적으로 수행한다.
2. 1의 과정을 모든 층에서 반복한 후에 출력층에서 계산된 값을 출력한다.
3. 손실함수를 사용하여 예측값(Prediction)과 실제값(Target)의 차이를 계산한다.
4. 경사하강법과 같은 방법과 역전파를 통해서 각 가중치를 갱신한다.
5. 학습 중지 기준을 만족할 때까지 위의 과정을 반복한다.

이때 1~4까지의 과정을 Iteration이라고 하며 매 Iteration마다 가중치가 갱신된다. Iteration은 순전파(1,2), 손실계산(3), 역전파(4)로 나눌 수 있다.

1. 순전파(Foward Propagation)

순전파는 입력층에서 입력된 신호가 은닉층의 연산을 거쳐 출력층에 값을 내보내는 과정이다. 각 층에서 이루어지는 연산 과정은 다음과 같다.

입력층(혹은 이전 은닉층)으로부터 신호를 전달받는다.
입력된 데이터에 가중치-편향 연산을 수행한다.
가중합을 통해 구해진 값은 활성화 함수를 통해 다음 층으로 전달된다.

가중치-편향 연산과 활성화 함수를 적용하는 과정을 수식적으로 나타내면 다음과 같다.

x^{(l+1)}_i = g(s^{(l)}_i) \\ \,\\ s^{(l)}_i = w^{(l)}_{0i} + w^{(l)}_{1i}x^{(l)}_{1} + w^{(l)}_{2i}x^{(l)}_{2}+\cdot\cdot\cdot\,+w^{(l)}_{(n-1)i}x^{(l)}_{n-1} + w^{(l)}_{ni}x^{(l)}_{n}

$g()$ : 활성화 함수

$l$ : Layer층 수

$i$ : Node 번호

$s^{(l)}_i$ : $l$ 번째 층 Layer에서 $(l+1)$ 번째 층 Layer의 i번째 노드로 출력되는 가중합

$w^{(l)}_{ji}$ : $l$ 번째 층 Layer의 $j$ 번째 Node에서 $(l+1)$ 번째 층의 $i$ 번째 node로 연결된 가중치

$x^{(l)}_{i}$ : $l$ 번째 층 Layer의 $i$ 번째 노드의 값

2. 손실함수(Loss function)

신경망은 손실 함수를 최소화 하는 방향으로 가중치를 갱신한다. 그렇기 때문에 손실 함수를 잘 정의해야 가중치가 제대로 갱신될 수 있다. 입력데이터를 신경망에 넣어 순전파를 거치면 마지막에는 출력층을 통과한 값이 도출된다. 이 때 출력된 값과 그 데이터의 타겟값을 손실 함수에 넣어 손실(Loss or Error)를 계산하게 된다.

대표적인 손실 함수로는 앞 서 배운 Section2에서 다루었던 MSE(Mean-Squared Error), CEE(Cross-Entropy Error) 등이 있다.

일반적으로 각 문제에서 사용하는 손실 함수가 있다.

📌 회귀: MSE, MAE

📌 이진 분류: binary_crossentropy

📌 다중 분류

One-Hot Encoding으로 라벨링 되었을 때: Categorical_crossentropy

Index 형식으로 라벨링 되었을 때: sparse_categorical_crossentropy

3. 역전파(Backward Propagation)

역전파(Backward Propagation)는 말 그대로 순전파와는 반대 방향으로 손실(Loss or Error) 정보를 전달해주는 과정이다.

순전파가 입력 신호 정보를 입력층부터 출력층까지 전달하여 값을 출력했다면, 역전파는 구해진 손실 정보를 이용하여 출력층부터 입력층까지 전달하여 각 가중치를 얼마나 업데이트 해야할 지를 구하는 알고리즘이다.

이 알고리즘을 수식으로 정리하여보았다.

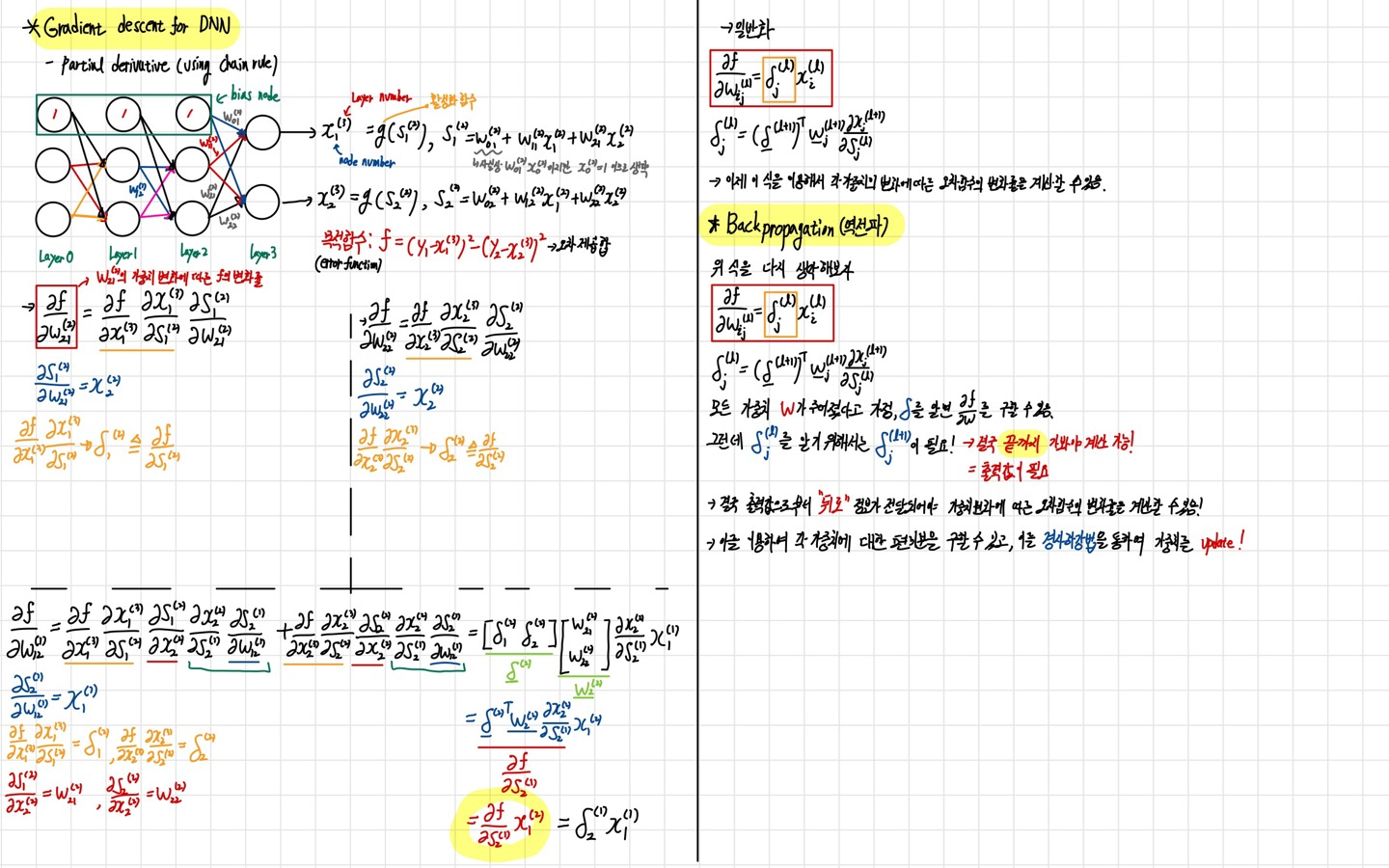
역전파 알고리즘의 수식에서 가장 중요한 것은 미분과 Chain Rule이다. 위의 그림에서도 복잡한 미분을 편미분을 통하여 각각의 변수에 대한 미분으로 나누어 진행하게 된다.

신경망은 매 반복마다 손실(Loss)을 줄이는 방향으로 가중치를 업데이트한다. 그리고 위의 그림에 설명하였듯이 손실을 줄이기 위해서 경사하강법(Gradient Descent), 확률적 경사하강법(Stochastic Gradient Descent, SGD), Mini-batch Gradient Descent 등의 옵티마이저(Optimizer) 사용한다.

4. 옵티마이저(Optimizer)

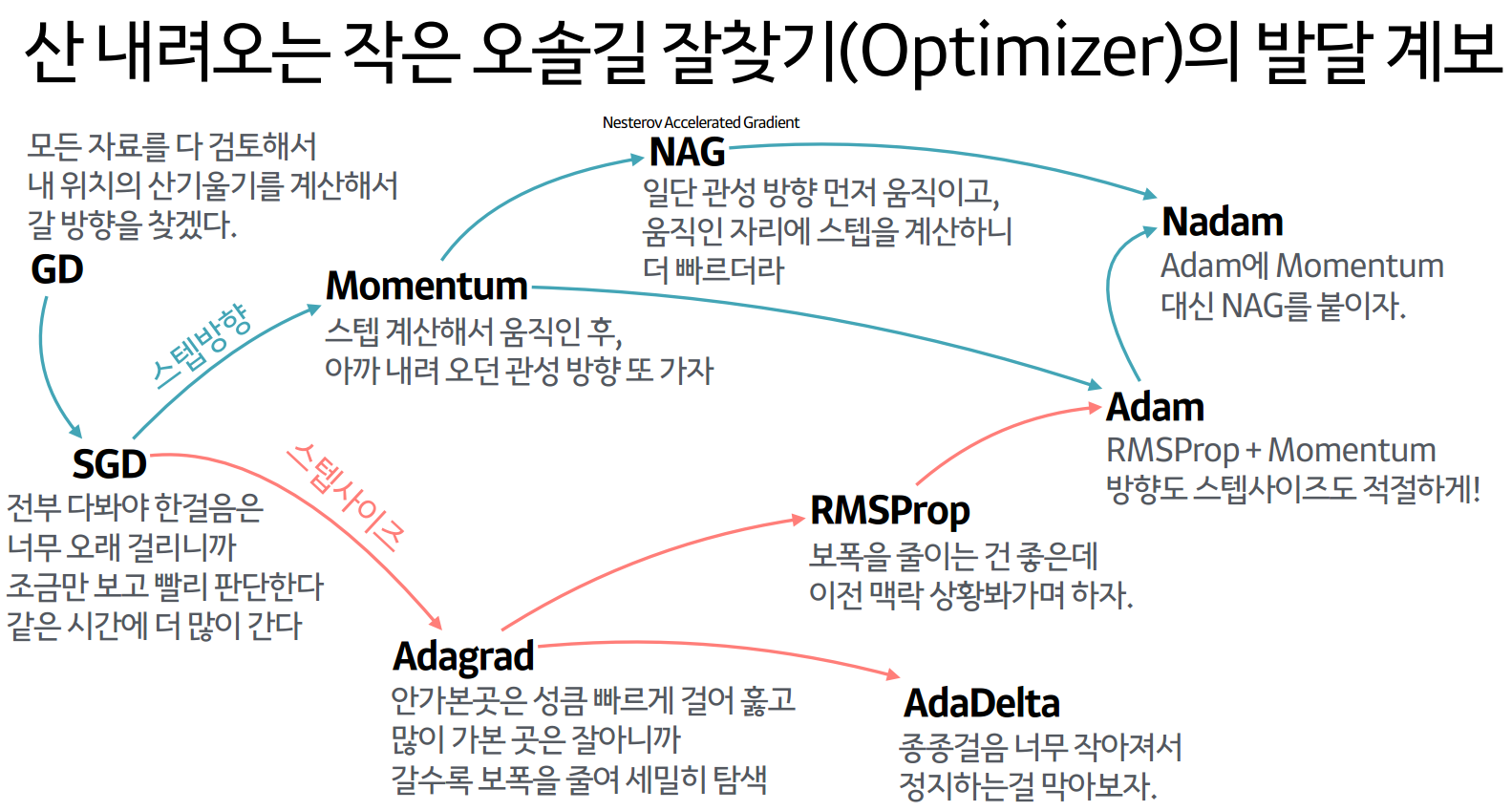
옵티마이저는 쉽게 말해 경사를 내려가는 방법을 결정한다.

4-1. 경사하강법(Gradient Descent, GD)

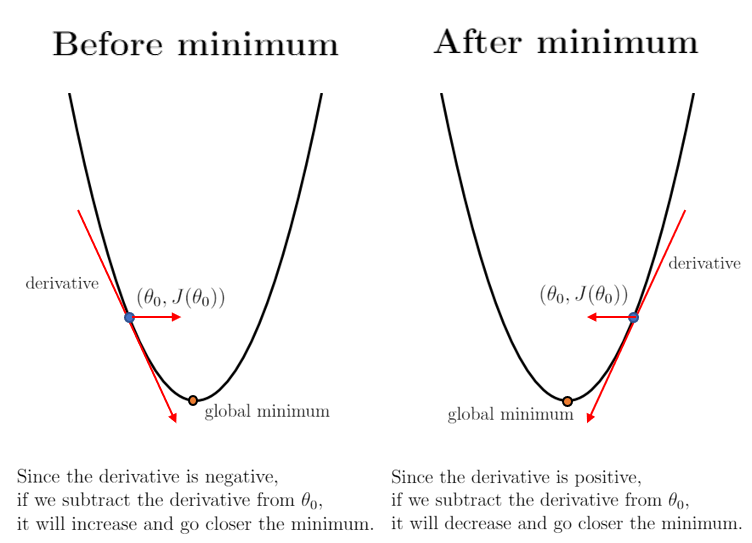
경사하강법은 앞의 N134에서 다루었었다. 다시 한 번 예시들어 설명하자면 앞이 보이지 않는 안개가 낀 산을 내려올 때, 모든 방향으로 산을 더듬어가며 산의 높이가 가장 낮아지는 방향으로 한 발씩 내딛어 가는 것이 경사하강법을 직관적으로 이해하기 가장 쉬운 예시이다.

오차함수가 최소가 되는 점을 찾기 위해서 미분을 활용한다. 경사하강법이라는 이름에서 알 수 있듯이 함수의 기울기를 활용하여 $\theta$ 의 값을 어디로 옮겼을 때 함수가 최솟값을 찾는지 알아본다.

일반적인 경사하강법에서는 모든 입력 데이터에 손실 함수의 기울기를 계산한 후에 가중치를 업데이트 하였다. 즉 1번의 Iteration마다 모든 데이터를 사용한다. 만약 입력데이터가 적다면 경사하강법으로도 빠르게 가중치를 금방 갱신할 수 있다.

자세한 수학적 공식과 알고리즘은 N134를 참고하자.

4-2. 확률적 경사하강법(Stochastic Gradient Descent, SGD)

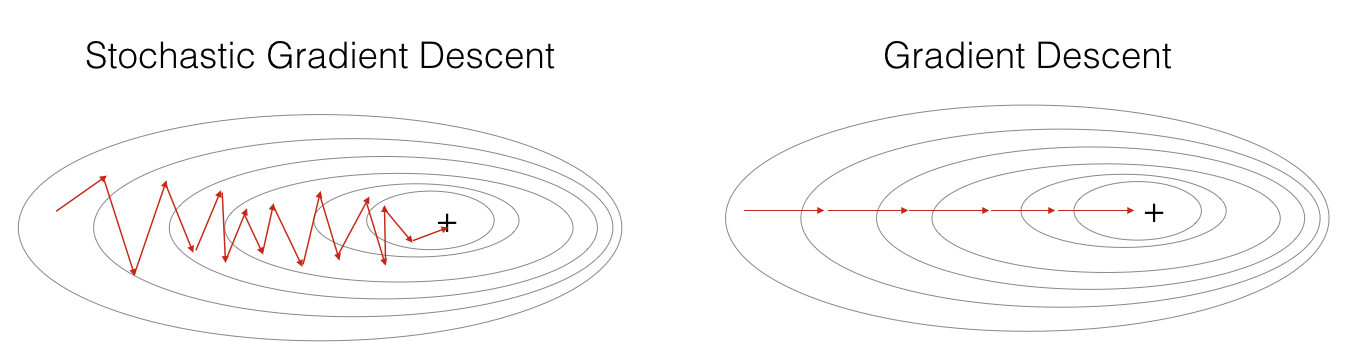
경사하강법의 경우 많은 양의 데이터를 다루게 되면 모든 데이터에 대해 손실을 계산하기 때문에 이 과정이 굉장히 오래 걸리게 된다. 그래서 등장한 것이 바로 확률적 경사 하강법과 미니 배치(Mini-batch) 경사 하강법이다.

확률적 경사하강법(SGD)은 전체 데이터에서 batch_size가 1인, 즉, 하나의 데이터만을 뽑아서 신경망에 입력한 후 손실을 계산한다. 그리고 그 손실 정보를 역전파하여 신경망의 가중치를 업데이트하게 된다.다시 말하면 1번의 Iteration에는 1개의 데이터만 사용하게 되고, 따라서 1번의 epoch에서 전체 데이터 수만큼의 Iteration이 진행된다.

각 Iteration에서 1개의 데이터만 사용하기 때문에 가중치를 빠르게 업데이트할 수 있다는 장점이 있다. 물론 확률적 경사 하강법에도 단점이 있다. 1개의 데이터만 보기 때문에 학습 과정에서 불안정한 경사 하강을 보인다.

4-3. Mini-batch Gradient Descent

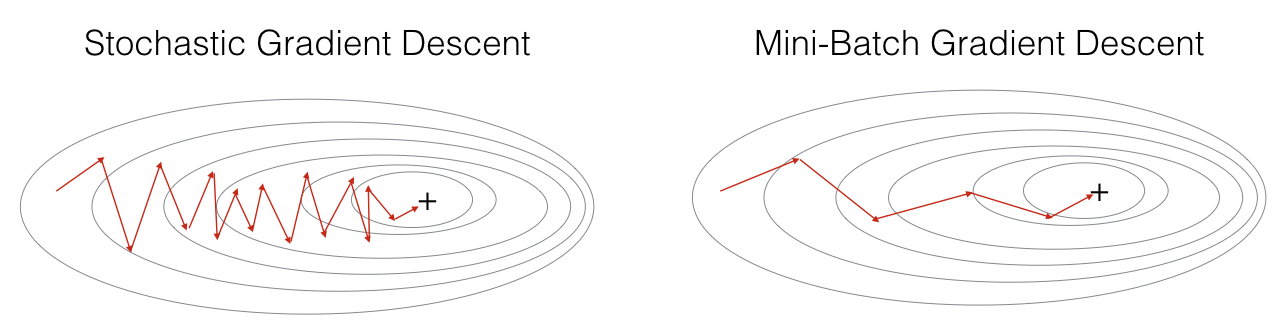
경사하강법의 단점과 확률적 경사하강법의 단점을 보완하기 위해서 그래서 두 방법을 적절히 융화한 Mini-batch Gradient Descent가 등장한다.

N개의 데이터로 미니 배치를 구성하여 해당 미니 배치를 신경망에 입력한 후 이 결과를 바탕으로 가중치를 업데이트 한다. 즉 1번의 Iteration마다 N개(=batch size)의 데이터를 사용하게 되고 결국 Iteration 수는 다음과 같이 결정된다.

Iteration = {\# \, of \, Data \over Batch\,Size}

이때, Keras에서는 전체 데이터를 batch_size로 나누었을 때 나머지가 생기면 그 나머지 그대로를 사용하여 Iteration 진행한다. 즉, 나눈 값을 올림하여 주면 1epoch에서의 전체Iteration 수가 된다.

일반적으로 batch_size는 2의 배수로 결정되먀, 메모리가 허락한다면 큰 사이즈를 쓰는 것이 안정적인 학습에 도움이 된다. 실제로는 32~128정도 사이의 크기가 주로 쓰인다고 한다.

위의 3가지 예시 외에도 다양한 옵티마이저들이 존재한다.

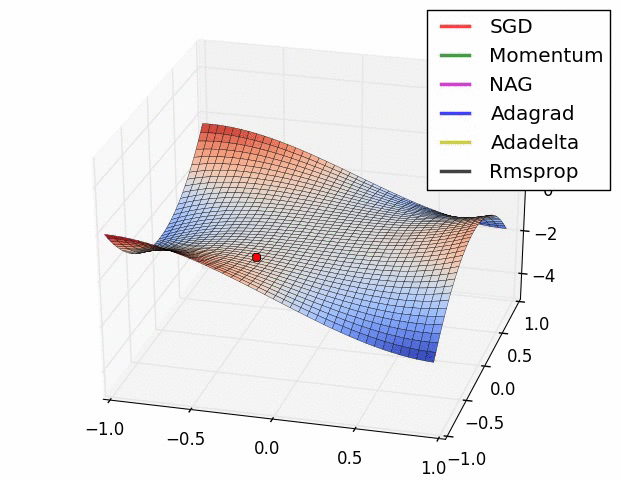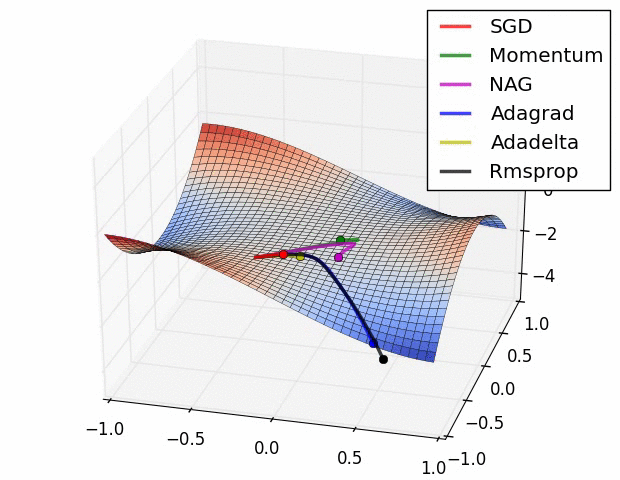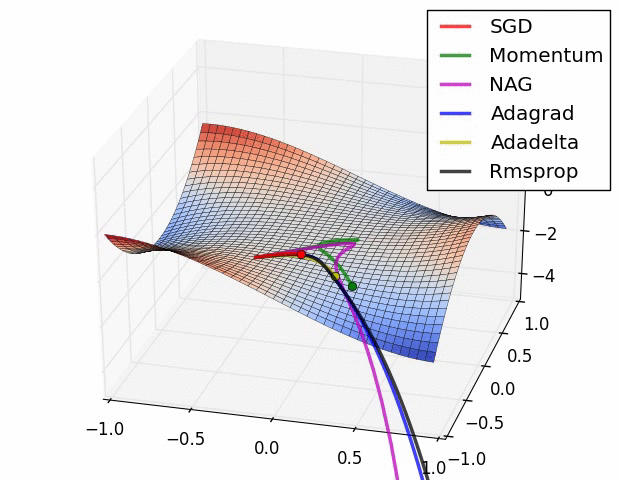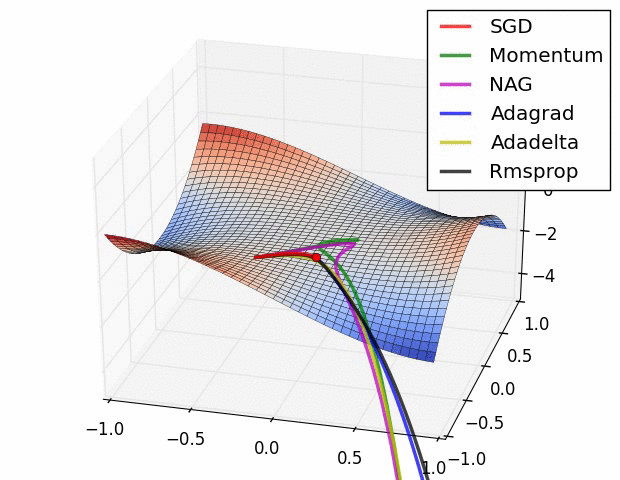
확률적 경사하강법(SGD)을 변형한 알고리즘: Momentum, RMSProp, Adam 등
Newton's method등의 2차 최적화 알고리즘 기반 방법: BFGS 등 (수치해석 책 참조하자.)

여러가지 옵티마이저 중에서 어떤 것이 가장 좋다고 말하기는 어렵다. 문제마다, 데이터마다 달라지기 때문에 여러 옵티마이저를 적용하면서 서로 비교하여 보아야 한다.

2. 회고

이번 Sprint는 뭔가 딥러닝을 위한 개념학습을 진행하는 것 같은 느낌이 든다. 레퍼런스에 다양한 수식과 파이썬으로 직접 신경망을 구성하는 코드들이 나와있는데, 아직 그것까지는 학습하지 못했다. 주말을 이용해서 추가적으로 학습해야할 것 같다.

그리고 뭔가 코드를 안만지니까 다시 전공 수업듣는 느낌이 든다. 조금 더 많은 딥러닝 알고리즘과 코드들을 만져보고 싶다.

Sea Panda

이전 포스트

[N411] TIL 및 회고

다음 포스트