[N532] TIL 및 회고(TIL이라 했지만 일주일이 지난..)

Sea Panda·2023년 3월 6일

코드스테이츠

부트캠프 TIL

목록 보기

44/46

학습내용

쾨니히스베르크의 다리 (링크)

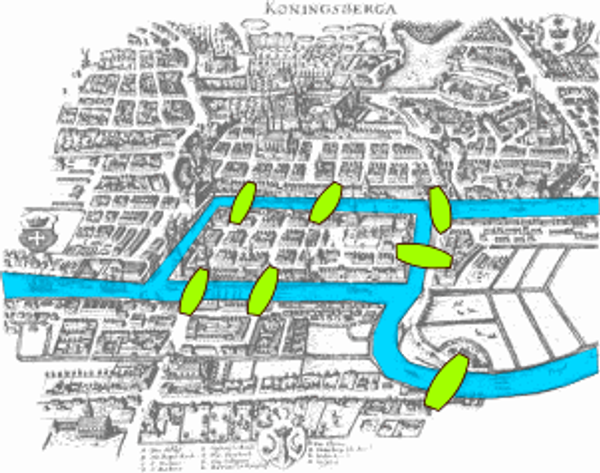
"임의의 지점에서 출발하여 일곱 개의 다리를 한 번씩만 건너서 원래 위치로 돌아오는 방법"에 대한 문제가 있었고, 많은 사람들이 이 문제의 답을 찾기 위해 노력을 했다.

그렇다면 정답은 무엇일까.

없다.

당시 레온하르트 오일러는 이 문제를 다음 그림과 형태로 각각의 다리에 a부터 g까지 이름을 부여하고 도식화했다.

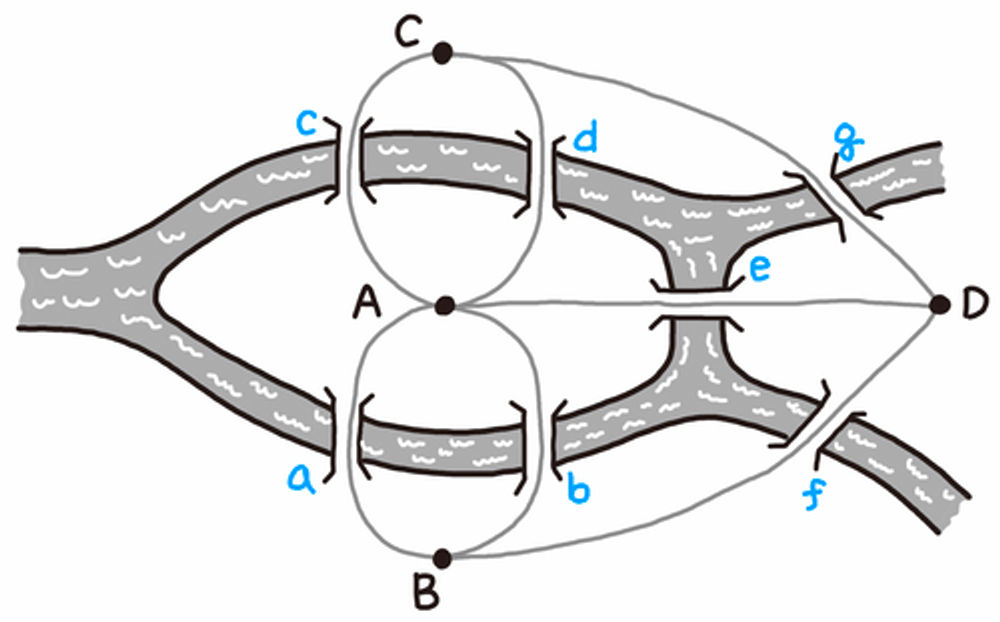
오일러의 스케치를 현대식 그래프 구조에 따라 나타낸 아래 그림에서는 A부터 D까지를 정점(Vertex), a부터 g까지는 간선(Edge)으로 구성된 그래프라는 수학적 구조를 찾아볼 수 있다.

그래프

정점(vertex=node)과 간선(=edge=link)으로 이루어진 자료구조
$G = (V, E)$

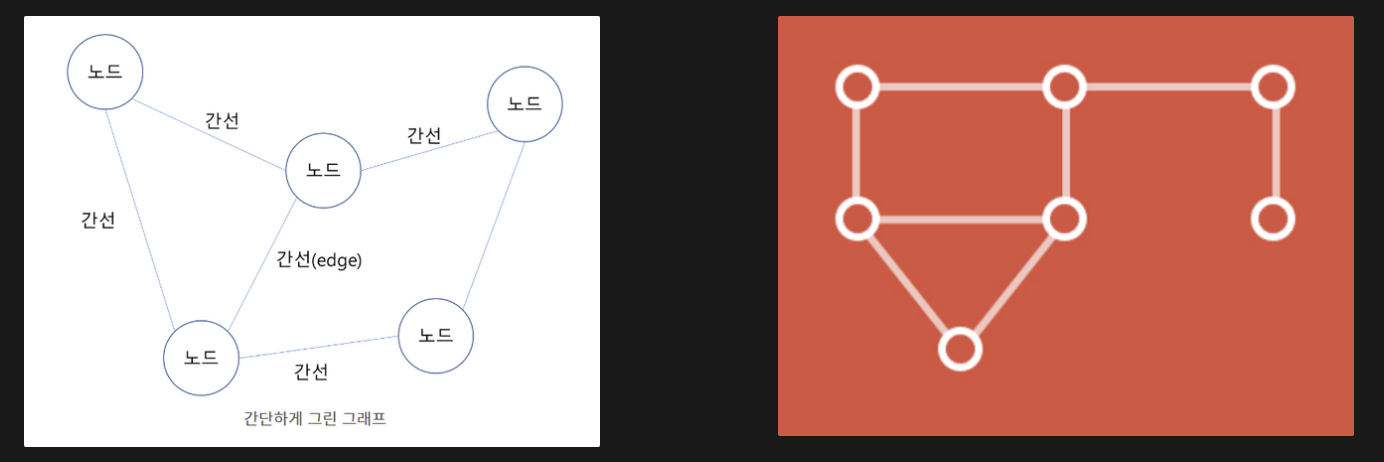
그래프의 유형

방향성, 순환, 가중치

그래프의 특성은 directed(방향성) 또는 undirected(무방향성) 그래프가 있다.
Directed Graph : 방향성이 있는 그래프이다. (유향 그래프 또는 방향성 그래프라고 불림)

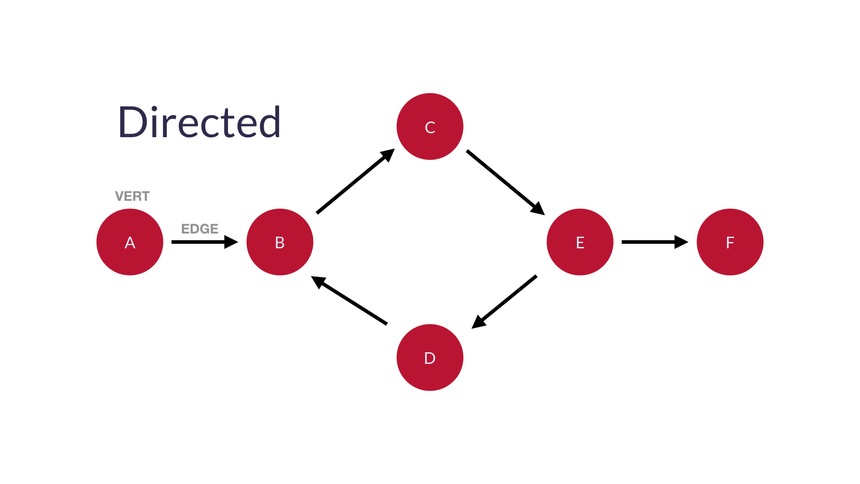
“한쪽 방향(one-way)”으로 설명될 수 있다면 directed가 가장 적합하다.
방향성그래프는 보는 것처럼 순서가 있으므로 마지막 노드(리프, leaf)가 있다. 위 그림에서는 'F'가 리프노드이다.
bidirectional(양방향)

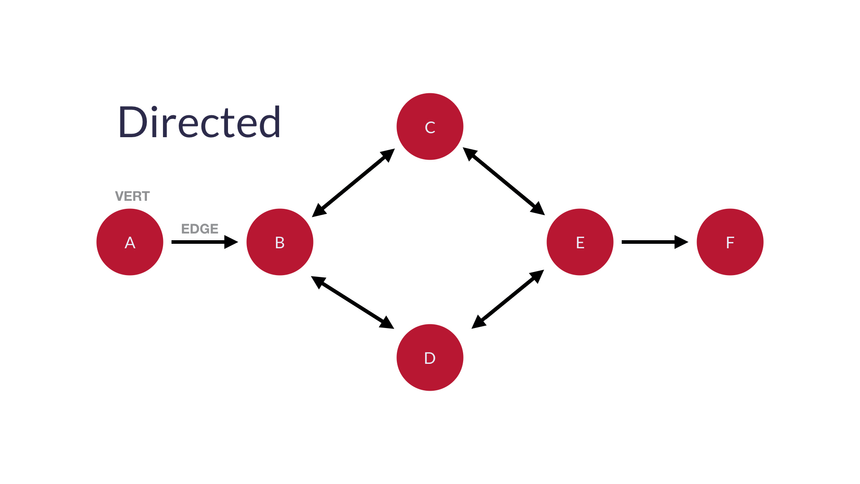
위처럼 Directed Graph는 양방향이 될 수 있다.

하지만 노드연결관계의 목적이 상호 교환이라면, undirected graph가 가장 적합하다.
- 상호 교환 : 화살표로 연결된 노드들이 서로 노드정보를 공유하는 것
Undirected Graph : 방향성이 없는 그래프이다.

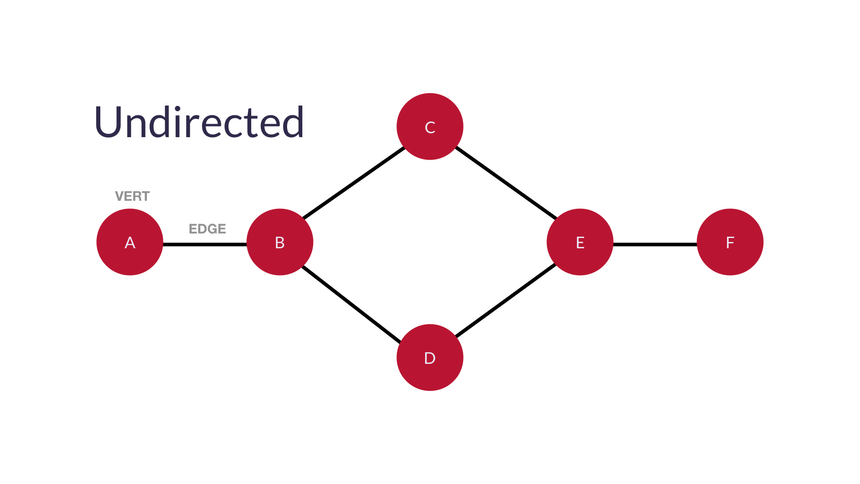
위처럼 무방향성은 방향(화살표)이 따로 지정되어있지 않다. 간선으로 연결된 노드들끼리 서로 인접(adjacent)해있다고 하며, 이웃(neighbor)라고 칭한다.
Weighted Graphs(가중 그래프)
- 가중 그래프에는 edge(간선)와 관련된 값이 있다.
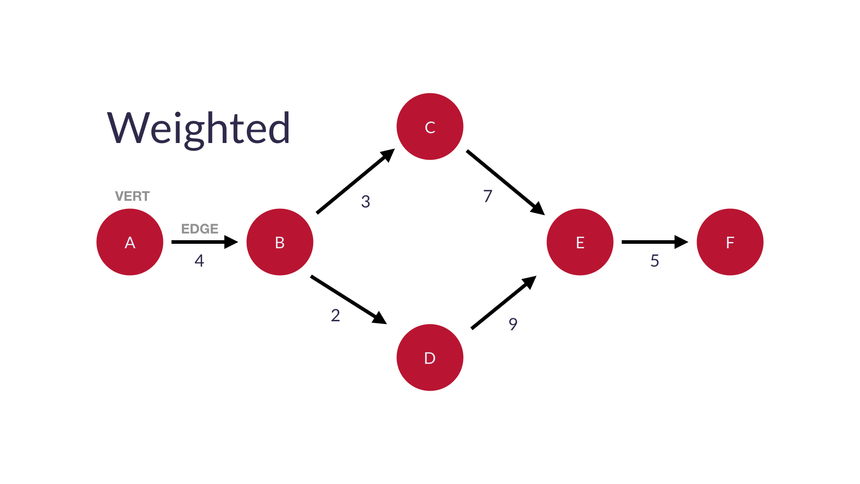
  - 각 edge의 가중치에 할당된 특정값을 호출한다.
  - 가중치는 서로 다른 그래프에서 서로 다른 데이터를 나타낸다.
  - 일상 예시
    - 교대역 —2분→ 강남역 —1분—>역삼역
Cyclic and Acyclic Graphs(순환 및 비순환 그래프)
- 순환(루프)을 형성할 수 있는 경우(예 : 방문한 노드에 다시 방문) 그래프는 순환 그래프이다.
  - 순환 그래프
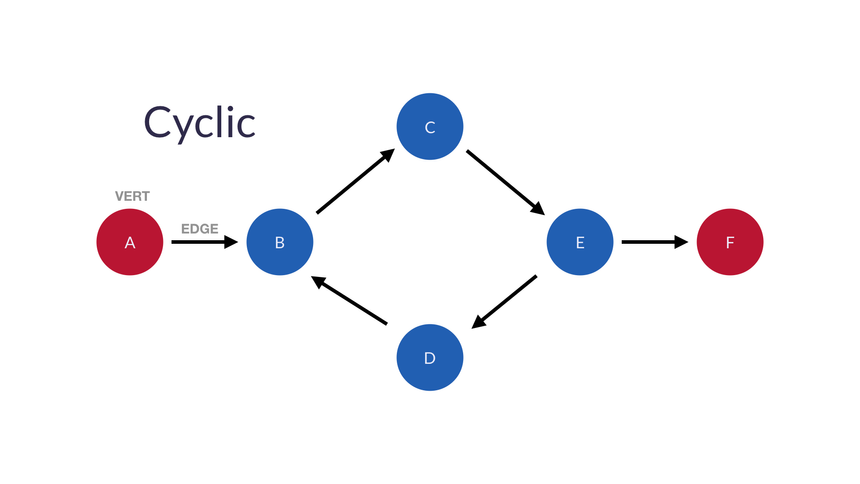
  - 비순환 그래프
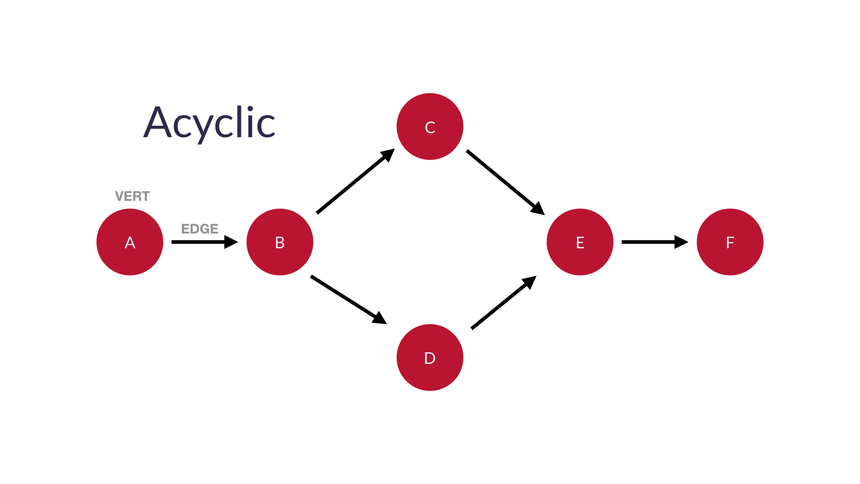
  - 참고 : undirected 그래프는 항상 동일한 노드에 재방문할 수 있으므로 순환 그래프이다.
  - 순환을 형성할 수 없는 경우(예 : 모서리를 따라 이미 방문한 노드에 방문할 수 없음) 비순환
    그래프라고 한다.
Directed Acyclic Graphs (DAGs) - 방향성 비순환 그래프
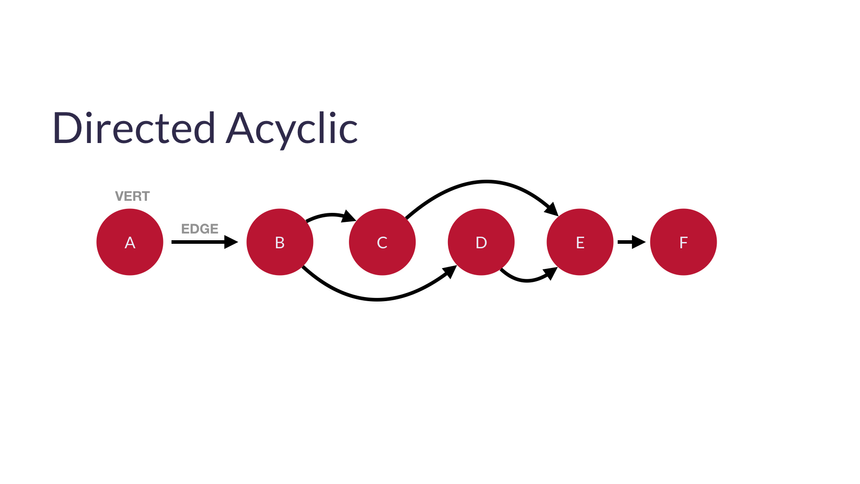
- 순환되지 않고 특정한 단방향 그래프이다.
- 그림처럼 edge가 순서대로 향하도록 DAG의 노드를 선형(단방향)으로 정렬할 수 있다.
- 트리도 DAGs의 일종이다.
- DAG는 작업들의 우선순위를 표현을 할 때 DAG를 많이 사용하게 된다.
  예를들어 공장에서 작업 스케줄링을 할 때 A 라는 작업이 끝나고 B를 해야하고 B 가 끝난 다음에는 C,D를 해야한다는 것을 DAG로 표현할 수 있다.
  - 활용 예시 : airflow DAG(링크)
- 또한 사이클이 없는 방향그래프라는 정의를 통해 모든 트리는 DAG임을 알 수 있다.
  (어떤 그래프가 주어졌을 때 이 그래프가 DAG인지 판단하기 위해서는 사이클의 존재여부를 확인하면 된다.)
  - 처음 출발한 노드(정점) v에서 시작하여 끝내 다시 v로 돌아가 순환 반복될 수 있는 방법이 없는 그래프라고 이해하면된다.

트리

트리의 특성: 루트가 있고, 아래로 차일드 노드들이 있고, 노드를 연결하는 엣지가 있고, 엣지의 방향성은 위에서 아래로 진핸된다.
트리는 그래프의 한 형태이다.
- 트리는 루트가 있고, 사이클이 없는, 아래로만 흐르는 방향그래프이다.

트리와 그래프의 차이

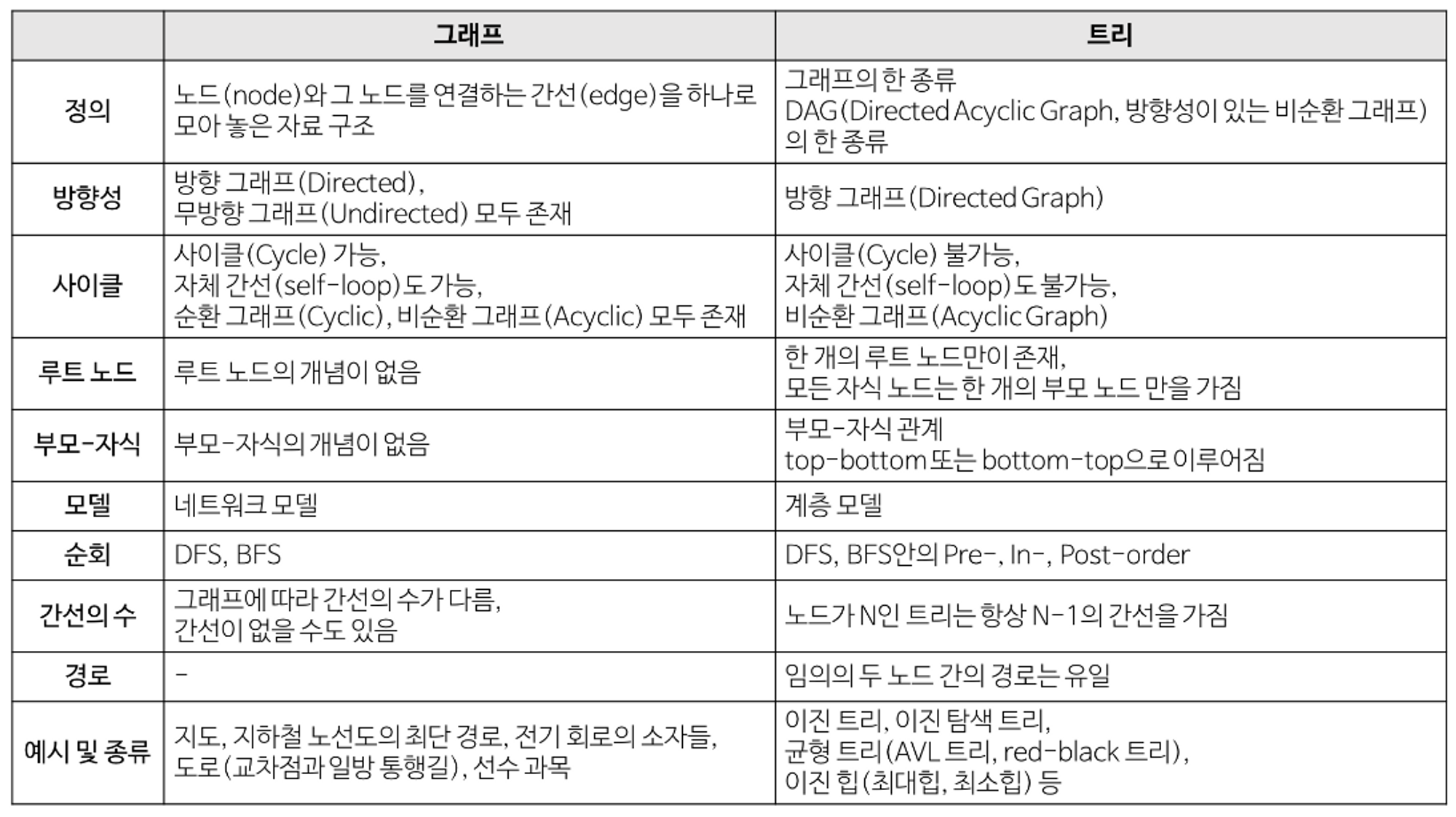
참고 : https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html

그래프의 활용

인접행렬, 인접리스트

그래프를 표현한다는 것은 인접성을 표현한다는 것을 이야기 합니다. 어떤 노드와 어떤 노드가 edge로 연결되어 있는지를 표현하는 것
두 노드가 간선으로 연결되어 있다면 ‘두 노드는 인접하다’라고 표현한다.

그래프를 나타내는 방법

인접행렬(adjacency matrices) : 이차원 배열에 표시하는 방법
인접리스트(adjacency lists) : 배열의 노드들을 나열하고 관계를 연결리스트로 표현하는 방법

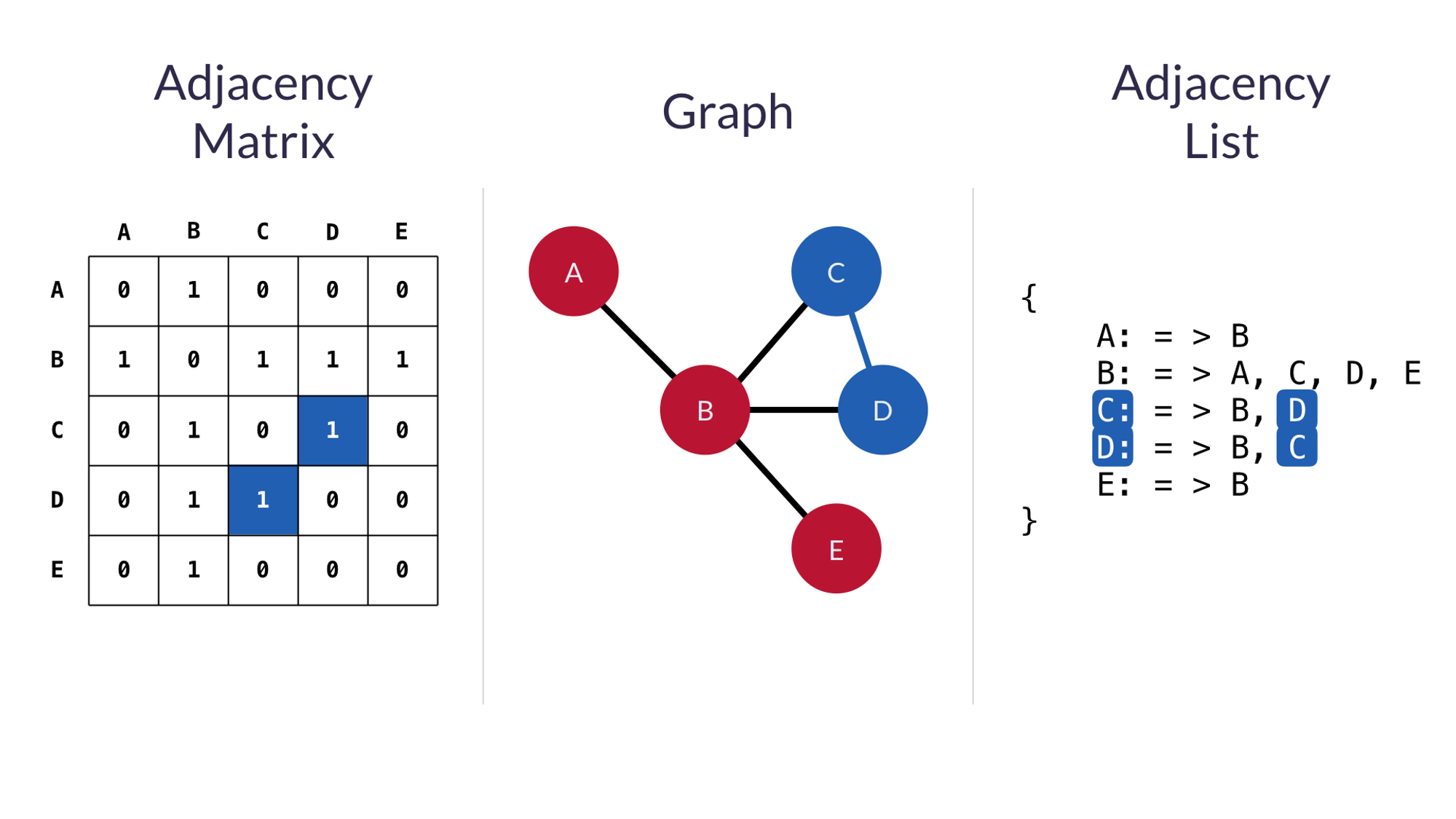
• 각 유형을 사용할 때, verts C와 D 사이의 관계를 어떻게 표현하는지가 중요하다.

인접행렬 (Adjacency Matrix)

인접 행렬은 표 형태로 표현하는 방법으로, 2차원 배열에 각 노드가 연결된 형태를 기록하는 방식이다.
파이썬에서는 2차원 리스트로 구현할 수 있다.

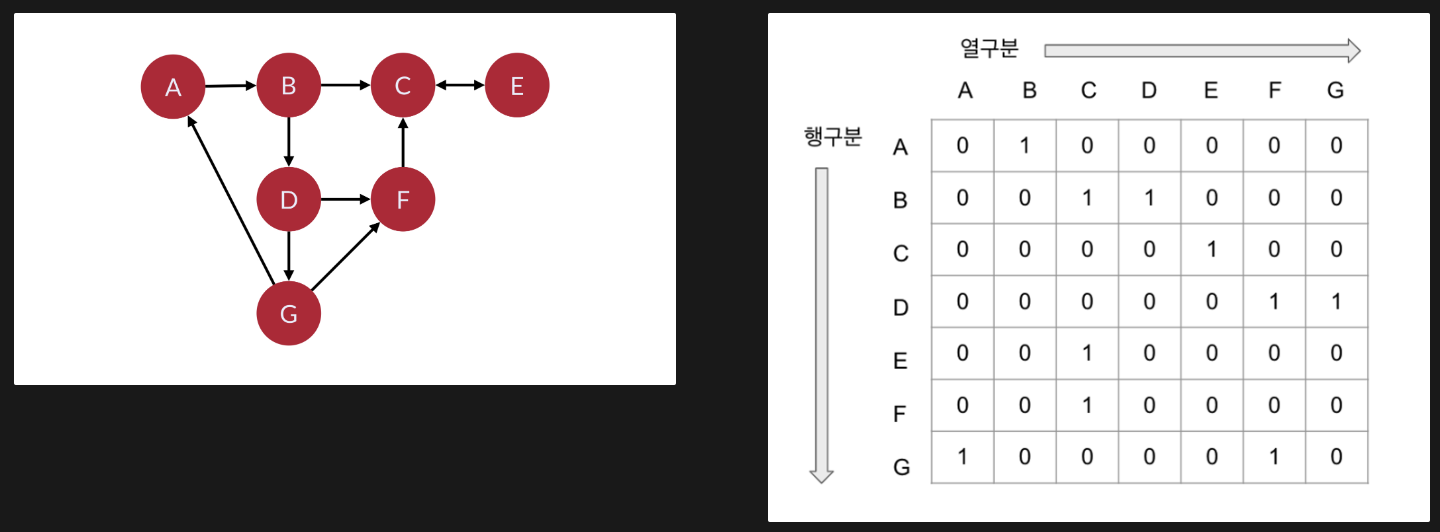
# 리스트로 구현한 인접행렬
# 아래 코드처럼 위의 간선 가중치는 1이다.
class Graph:
    def __init__(self):
        self.edges = [[0,1,0,0,0,0,0],
                      [0,0,1,1,0,0,0],
                      [0,0,0,0,1,0,0],
                      [0,0,0,0,0,1,1],
                      [0,0,1,0,0,0,0],
                      [0,0,1,0,0,0,0],
                      [1,0,0,0,0,1,0]]

노드가 n개면 n by n 행렬을 만들게 된다.

인접리스트(Adjacency List)

인접리스트에서 그래프는 전체 노드 목록을 저장한다. 노드와 인접한 노드들을 연결리스트로 쭉 나열하여 저장하는 것

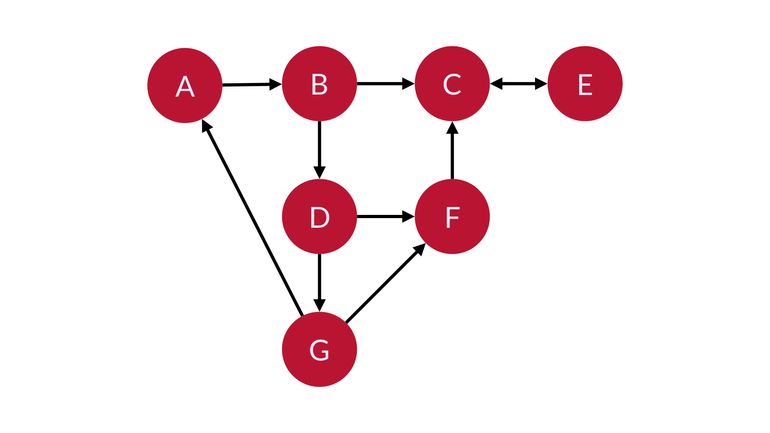
# 위 그림에 대해 딕셔너리를 사용한 인접리스트 예시
# 노드가 키가 되고, 인접노드가 값이 되는 딕셔너리이다.
# 가장자리 노드들은 set으로 구현되어 있다.
class Graph:
    def __init__(self):
        self.vertices = {
                            "A": {"B"},      # 여기서 {"B"}가 set의 형태이다.
                            "B": {"C", "D"}, # {"B" : {}}의 형태는 딕셔너리
                            "C": {"E"},      # 즉, 딕셔너리 안에 set이 있는 것이다.
                            "D": {"F", "G"},
                            "E": {"C"},
                            "F": {"C"},
                            "G": {"A", "F"}
                        }

메모리 측면에서 보자면 인접 행렬 방식은 모든 관계를 저장하므로 노드 개수가 많을수록 메모리가 불필요하게 낭비된다.
반면에 인접리스트 방식은 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용한다.
하지만 인접 리스트 방식은 연결된 데이터를 하나씩 확인해야 하기 때문에, 인접 행렬 방식에 비해 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느리다.

예시 퀴즈 (1)

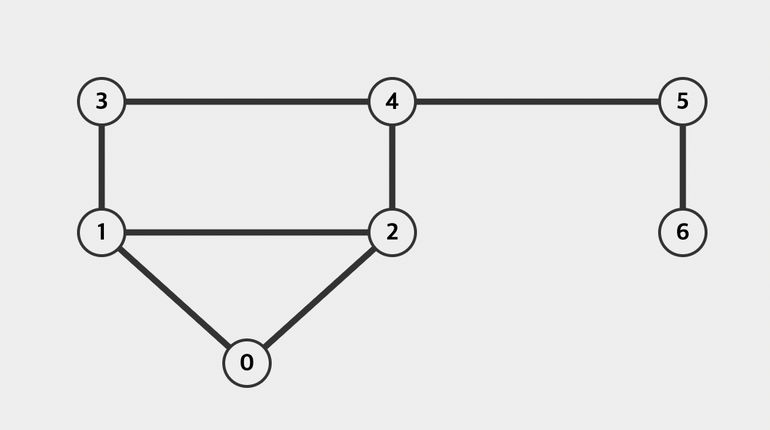
위 사진의 그래프를 인접행렬과 인접 리스트로 나타내어보아라.

# 무방향 그래프

# 인접 행렬
graph = [#0 1 2 3 4 5 6
         [0,0,0,0,0,0,0], # 0
         [0,0,0,0,0,0,0], # 1
         [0,0,0,0,0,0,0], # 2
         [0,0,0,0,0,0,0], # 3
         [0,0,0,0,0,0,0], # 4
         [0,0,0,0,0,0,0], # 5
         [0,0,0,0,0,0,0]  # 6
        ]

# 인접 리스트
graph = {
    0: {},
    1: {},
    2: {},
    3: {},
    4: {},
    5: {},
    6: {}
}

정답

graph = [# 0 1 2 3 4 5 6
		   [0,1,1,0,0,0,0], #0
		   [1,0,1,1,0,0,0], #1
		   [1,1,0,0,1,0,0], #2
		   [0,1,0,0,1,0,0], #3
		   [0,0,1,1,0,1,0], #4
		   [0,0,0,0,1,0,1], #5
		   [0,0,0,0,0,1,0]  #6
		]
        
graph = {
    0: {1, 2},
    1: {0, 2, 3},
    2: {0, 1, 4},
    3: {1, 4},
    4: {2, 3, 5},
    5: {4, 6},
    6: {5}
}

예시 퀴즈 (2)

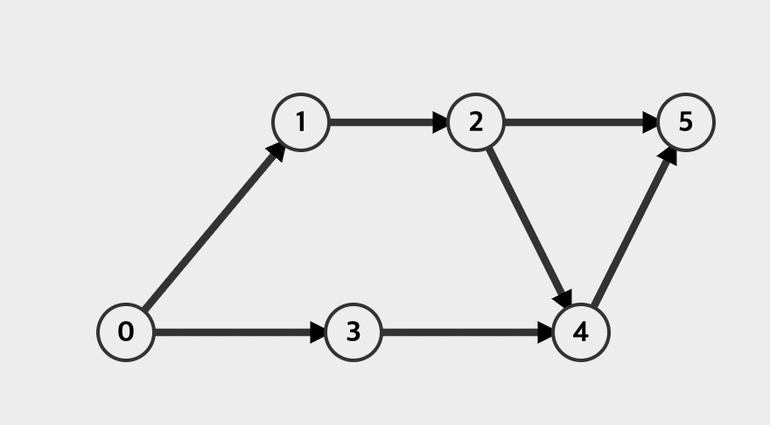
# 단방향 그래프

# 인접행렬
graph = [#0 1 2 3 4 5
         [0,0,0,0,0,0], # 0
         [0,0,0,0,0,0], # 1
         [0,0,0,0,0,0], # 2
         [0,0,0,0,0,0], # 3
         [0,0,0,0,0,0], # 4
         [0,0,0,0,0,0]  # 5
        ]

# 인접리스트
graph = {
    0: {},
    1: {},
    2: {},
    3: {},
    4: {},
    5: {}
}

정답

graph = [#0 1 2 3 4 5
         [0,1,0,1,0,0], # 0
         [0,0,1,0,0,0], # 1
         [0,0,0,0,1,1], # 2
         [0,0,0,0,1,0], # 3
         [0,0,0,0,0,1], # 4
         [0,0,0,0,0,0]  # 5
        ]

# 인접리스트
graph = {
    0: {1, 3},
    1: {2},
    2: {4,5},
    3: {4},
    4: {5},
    5: {}
}

순회(Traversal)

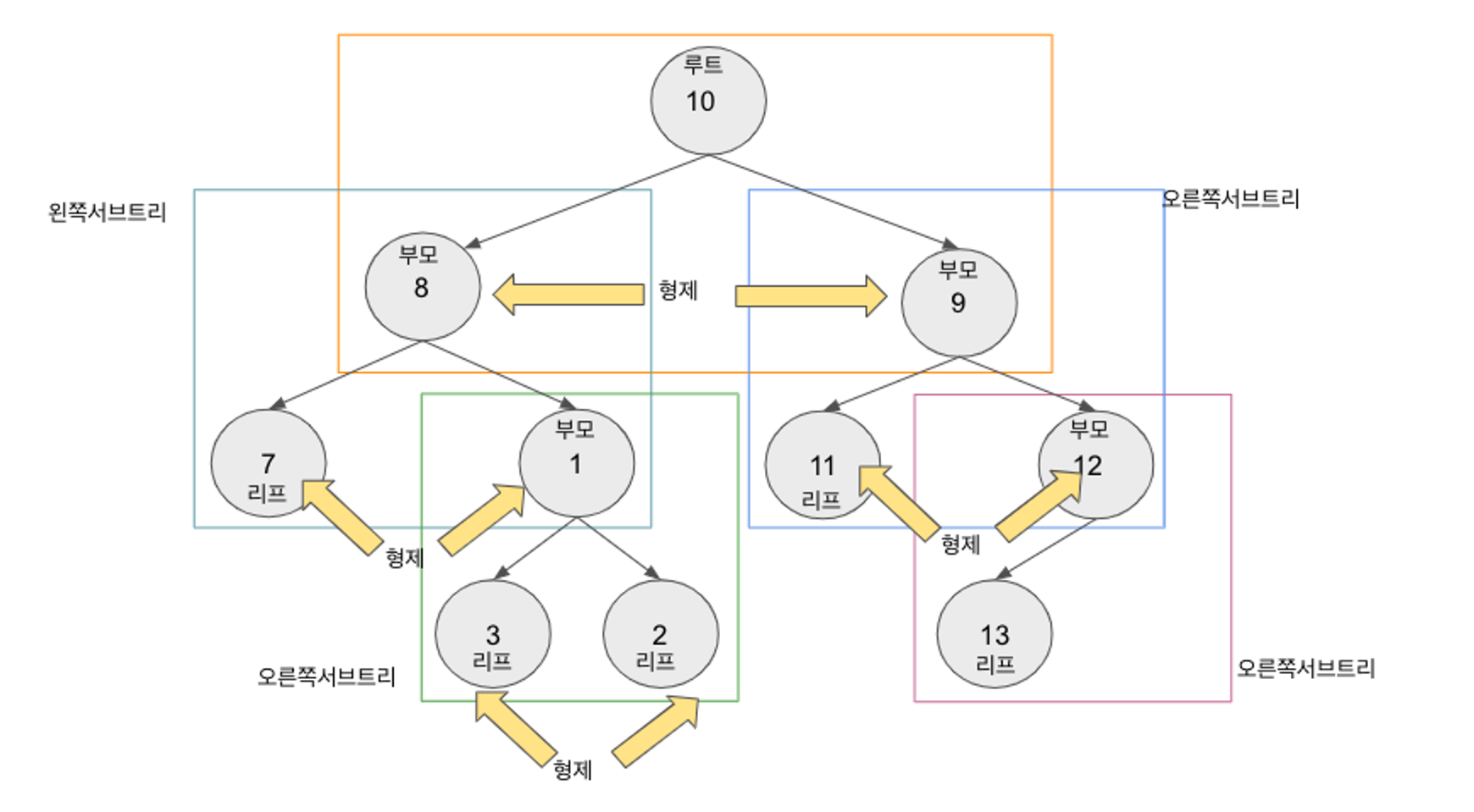
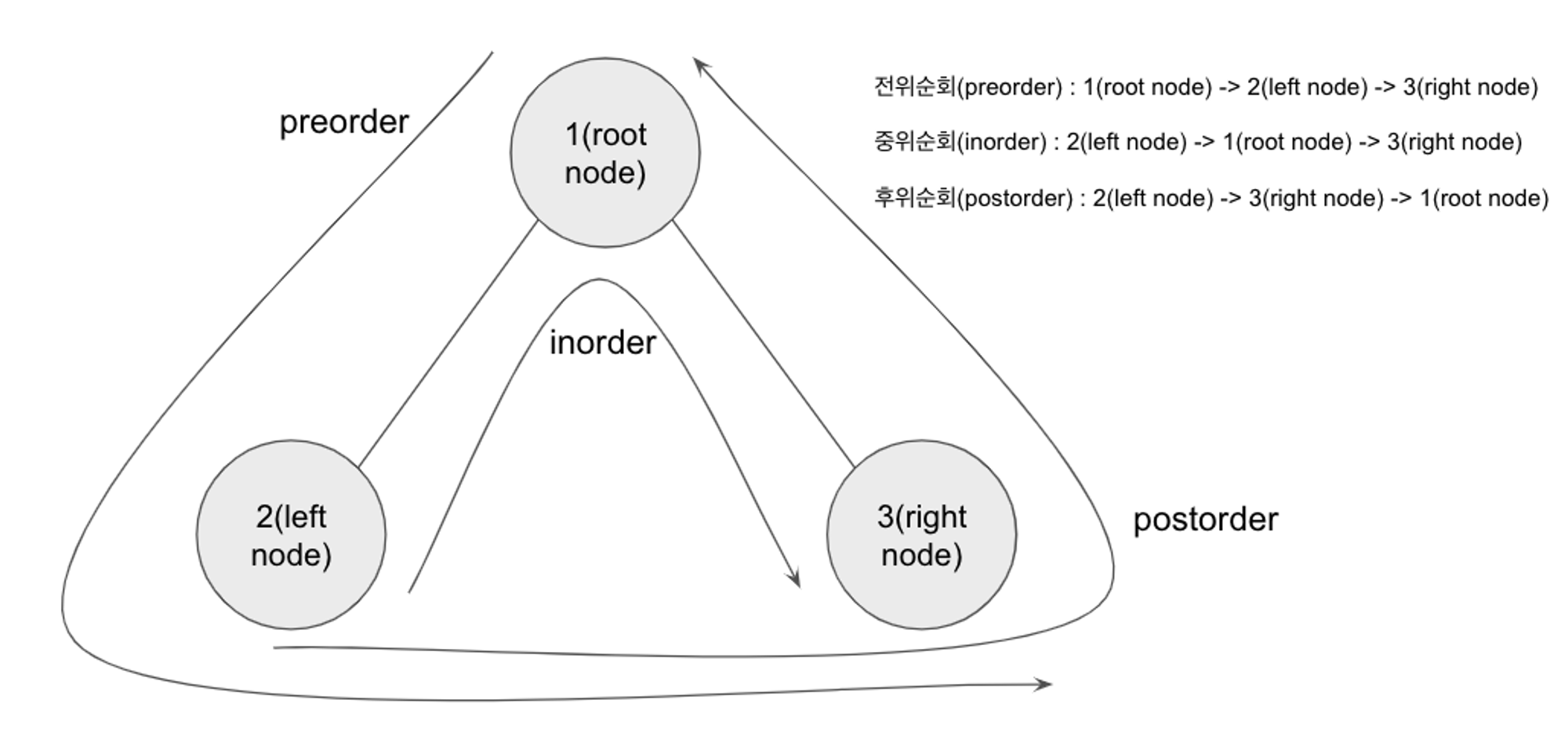
순회 화살표를 잘 보자.

순회 기본개념

순회는 Traversal로 명명되며, 그래프 또는 트리처럼 연결된 구조에서 노드를 한 번씩 탐색하는 개념이다.
- 순회의 목적은 모든 노드 또는 특정 노드를 방문하는 방법을 찾는 것이다.
- BST(이진검색트리)와 다른 규칙이 적용되며 방향에 따라 탐색방법이 달라질 수 있다.

그래프와 트리의 순회구분

트리의 순회(전위, 중위, 후위)

그래프의 순회는 DFS(깊이우선탐색), BFS(너비우선탐색) 방법이 있다.
- DFS, BFS는 탐색 알고리즘이다.
  - 그래프는 루트, 부모, 자식노드 개념이 없지만 전위, 중위, 후위 순회의 순회개념을 활용하여 DFS, BFS를 구현할 수 있다.
트리의 순회는 전위, 중위, 후위순회이다.
- 전위순회(preorder traverse): 루트를 먼저 방문 , root node → left node → right node
- 중위순회(inorder traverse): 왼쪽 서브트리를 방문 후 루트 방문, left → root → right
- 후위순회(postorder traverse): 왼쪽 서브트리, 오른쪽 서브트리, 루트 방문, left → right → root

순회 실습 해보기

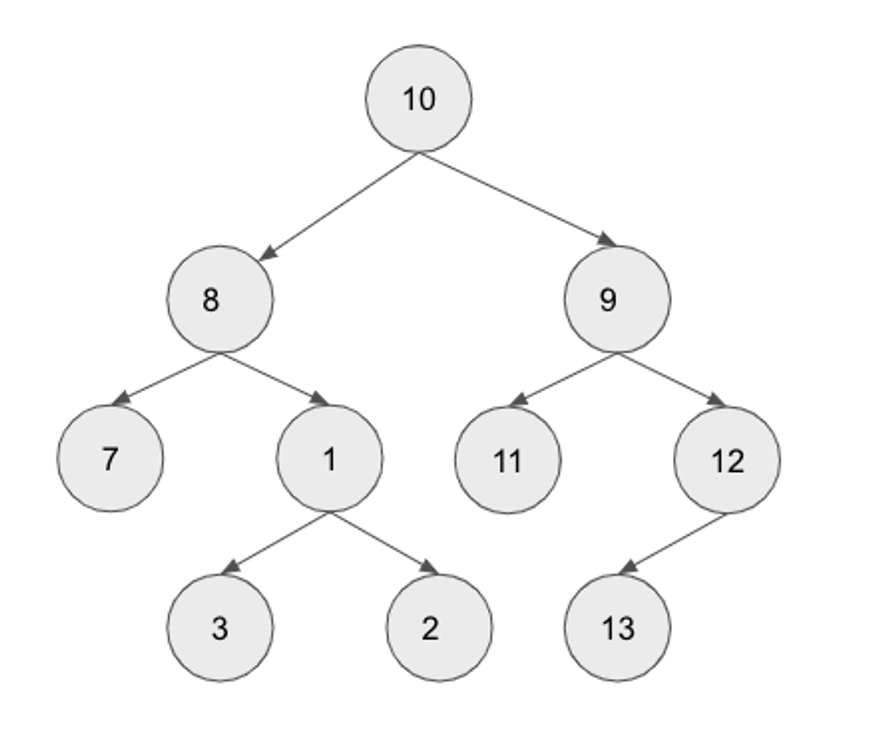
# 이진 트리의 노드 클래스
class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

# 전위 순회(pre-order) 함수
def preOrder(root):
    if root:
        print(root.val, end=" ")
        preOrder(root.left)
        preOrder(root.right)

# 중위 순회(in-order) 함수
def inOrder(root):
    if root:
        inOrder(root.left)
        print(root.val, end=" ")
        inOrder(root.right)

# 후위 순회(post-order) 함수
def postOrder(root):
    if root:
        postOrder(root.left)
        postOrder(root.right)
        print(root.val, end=" ")

root = TreeNode(10)
root.left = TreeNode(8)
root.right = TreeNode(9)
root.left.left = TreeNode(7)
root.left.right = TreeNode(1)
root.right.left = TreeNode(11)
root.right.right = TreeNode(12)
root.left.right.left = TreeNode(3)
root.left.right.right = TreeNode(2)
root.right.right.left = TreeNode(13)

preOrder(root) # 전위 순회
print(" ")
inOrder(root)  # 중위 순회
print(" ")
postOrder(root) # 후위 순회

결과가 아래와 같은지 확인해 봅시다.

전위순회 결과: 10 8 7 1 3 2 9 11 12 13

중위순회 결과: 7 8 3 1 2 10 11 9 13 12

후위순회 결과: 7 3 2 1 8 11 13 12 9 10

인접행렬, 인접리스트 구현하기

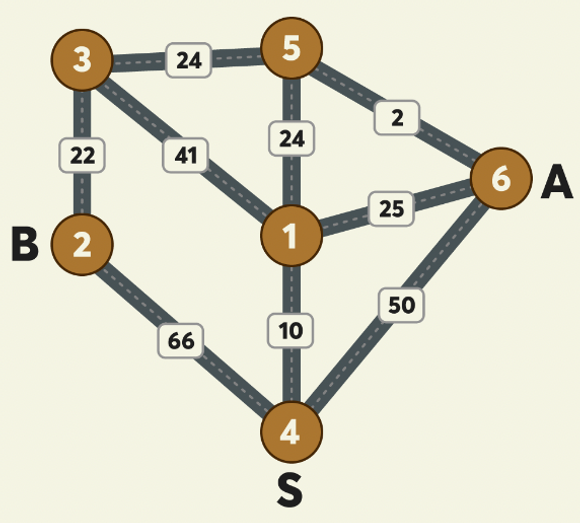
# 인접 행렬
input_list = [
[4, 1, 10], # 노드4번에서 노드1번으로 연결되는 가중치가 10입니다.
[3, 5, 24],
[5, 6, 2],
[3, 1, 41],
[5, 1, 24],
[4, 6, 50],
[2, 4, 66],
[2, 3, 22],
[1, 6, 25]
]

arr = [[0 for col in range(6)] for row in range(6)]

for a, b, c in input_list:
		arr[a-1][b-1] = c

arr

# 인접 리스트

adj_dict = {}

for a,b,c in input_list:
		if a in adj_dict:
			adj_dict[a].update({b:c})
		else:
			adj_dict.update({a: {b:c}})

회고

사실 정리도 되게 오랜만에 하는 것 같다. 그간 다양한 일이 있었는데 일단 Section4 Project를 진행했고 Section5가 종료되었다. Section5는 CS파트로 자료구조와 알고리즘을 학습했다. 앞으로 프로젝트까지 약 3일?에서 4일 정도 남았는데 그간 정리 못한 파트들을 몰아서 정리할 계획이다.

참고로 N532부터 N534는 내가 정리한 내용이 아닌 코치님께서 정리해주신 내용을 사실상 싸악 긁어서 Velog에서 정상적으로 보이게 편집만 한 것이다.

이야기가 잠깐 딴 길로 갔는데, 일단 3일동안 배운 내용 복습하는 겸 정리할 계획이다. 최종적으로는 이 글이 N531뒤에 오겠지만, 작성은 Section5에서 어떤 글보다 먼저했다...

그리고 오늘 빅데이터분석기사 필기접수로 디스코드에서 동기분들이 이야기하시던데 나는 일단 일반기계기사를 공부하면서 고민을 좀 해봐야겠다. 원래는 전공을 아예 내팽겨치고 분야를 갈아타려했는데, 그것보다는 내 전공을 살리면서 인공지능을 다루면 보다 더 좋을 것 같아서 일단 병행하면서 공부할 계획이다.

영어 공부도 하려고 시원스쿨 학습지도 샀는데... 공부할 것들은 쌓아놓고 해결하지 못하는 것 같다. 진짜 다시 정신차리고 열심히 살아보자...

❗️참고자료
1. 코드스테이츠 교육자료

Sea Panda

이전 포스트

[N531] 내용정리

다음 포스트