LSD vs MSD
앞서 설명한 LSD와 반대로
MSD는 Most Significant Digit의 약자로써 가장 중요한 자릿수, 다시말해서 가장 큰 자릿수부터 정렬이 진행된다는 의미를 담고 있다.
"그럼 LSD와 방향만 다르고 정렬과정은 같나요!?"
안타깝지만.. 아니다..
이를 확인하기위해 LSD방식으로 큰 자릿수부터 정렬을 진행해보겠다.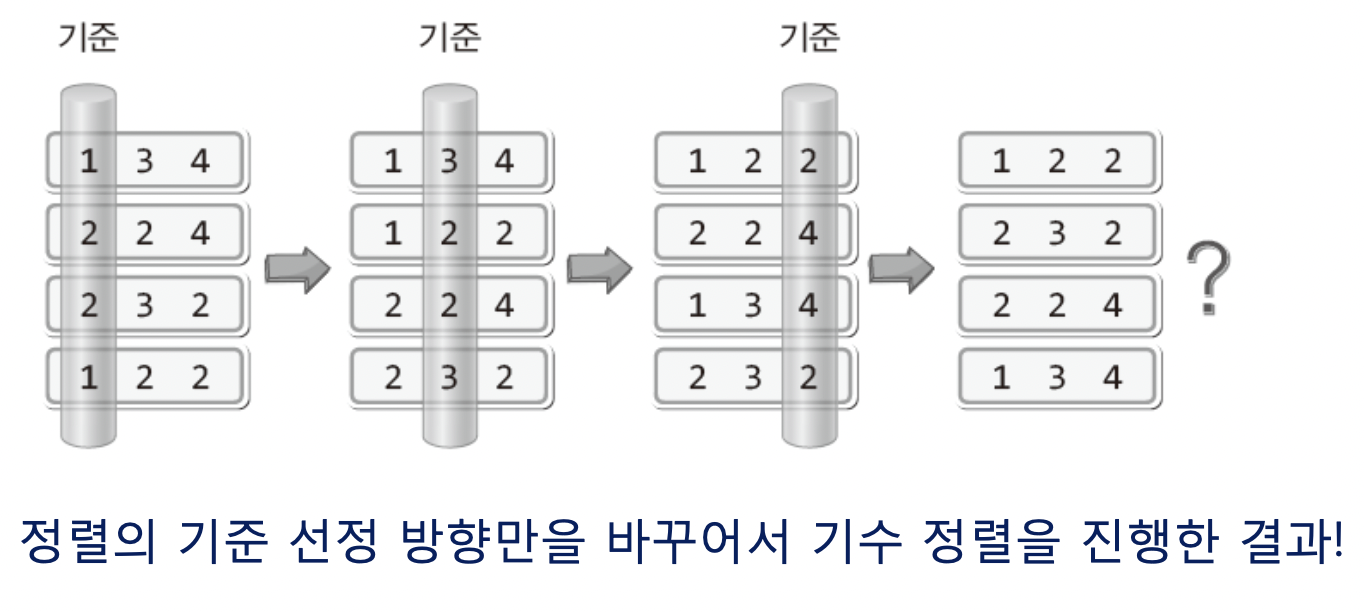 
완전 이상하게 정렬되지 않았는가!
MSD는 가장 큰 자릿수에서부터 정렬을 시작하기에
첫 번째 과정만 거쳐도 대략적인 정렬의 결과가 눈에 보인다.
즉, LSD는 마지막에 가서 정렬 순서를 판단하는 반면, MSD는 점진적으로 정렬을 완성해내간다.
따라서 MSD방식의 가장 큰 장점은
"반드시 끝까지 가지 않아도 된다. 중간에 정렬이 완료될 수도 있다." 이다!
이렇듯 마지막 까지 비교를 하지 않아도 되니 성능적 이점을 기대할 수 있으나...
단점이 존재한다.
"모든 데이터에 일괄적인 과정을 거치게 할 수 없습니다."
즉, 중간에 데이터를 점검하지 않으면 224,232 와 같이 두번째 단계에서 이미 대소가 결정됐는데도 자리를 바꾸는 경우가 발생한다.
그렇기에 중간에 데이터를 점검해야하기때문에 구현의 난이도가 LSD에 비해 상대적으로 높다. 그리고 성능의 이점이 반감될 수도 있다.
기수정렬 : LSD 기준 구현
일반적으로 "기수 정렬" 이라 하면 LSD방식을 기준으로 이야기한다.
이는 "구현의 편의성"이 가장 큰 이유일것이다!
"MSD가 성능 더 좋지 않나요..?" 라는 의문이 생길것이다.
그렇지 않다! 빅-오는 동일하고 정렬의 과정이 단축되어 성능의 향상을 조금이라도 기대할 수 있지만 추가적인 연산과 별도의 메모리가 요구 되기때문에 일반적인 상황이라면 굳이 MSD 보단 LSD방식을 따른다.
양의 정수라면 그 길이에 상관없이 정렬하는 기수정렬을 만들자!
42, 175
어떤가!
2와5를 비교후 4와 7를 비교후!
마지막 세번째 자릿수는 !
0과 1을 비교하면된다!
딱히 어렵지 않은 수식이다 !
이제 기수정렬소스를 구현해보자!
아!
양동이는 그 구조가 큐에 해당하기에 "연결 리스트 기반의큐"를 활용해야한다!!
#include <stdio.h>
#include "ListBaseQueue.h"
#define BUCKET_NUM 10
void RadixSort(int arr[],int num, int maxLen)
{
// 매개변수 maxLen에는 정렬대상 중 가장 긴 데이터의 길이 정보가 전달
Queue bukets[BUCKET_NUM];
int bi;
int pos;
int di;
int divfac = 1;
int radix;
// 10 개의 버킷 초기화
for(bi =0; bi<BUCKET_NUM; bi++)
QueueInit(&bukets[bi]);
//가장 긴 데이터의 길이만큼 반복
for(pos=0;pos<maxLen;pos++)
{
//정렬대상의 수만큼 반복
for(di=0;di<num;di++)
{
//N번째 자리의 숫자 추출
radix = (arr[di]/divfac)%10;
// 추출한 숫자를 근거로 법킷에 데이터 저장
Enqueue(&bukets[radix], arr[di]);
}
// 버킷 수만큼 반복
for(bi=0,di=0;bi<BUCKET_NUM;bi++)
{
//버킷에 저장된 것 순서대로 다 꺼내서 다시 arr에 저장
while(!QIsEmpty(&bukets[bi]))
arr[di++] = Dequeue(&bukets[bi]);
}
// N번째 자리의 숫자 추출을 위한 피제수 증가
divfac *= 10;
}
}
int main(void)
{
int arr[7]={13,212,14,7141,10987,6,15};
int len = sizeof(arr)/sizeof(int);
int i;
;
RadixSort(arr, len, 5);
for(i=0;i<len;i++)
printf("%d ",arr[i]);
printf("\n");
return 0;
}추가 필요 파일: ListBaseQueue.c,h
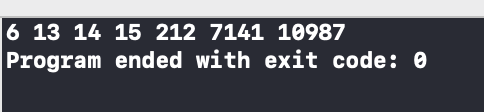
성공적으로 돌아간다 !
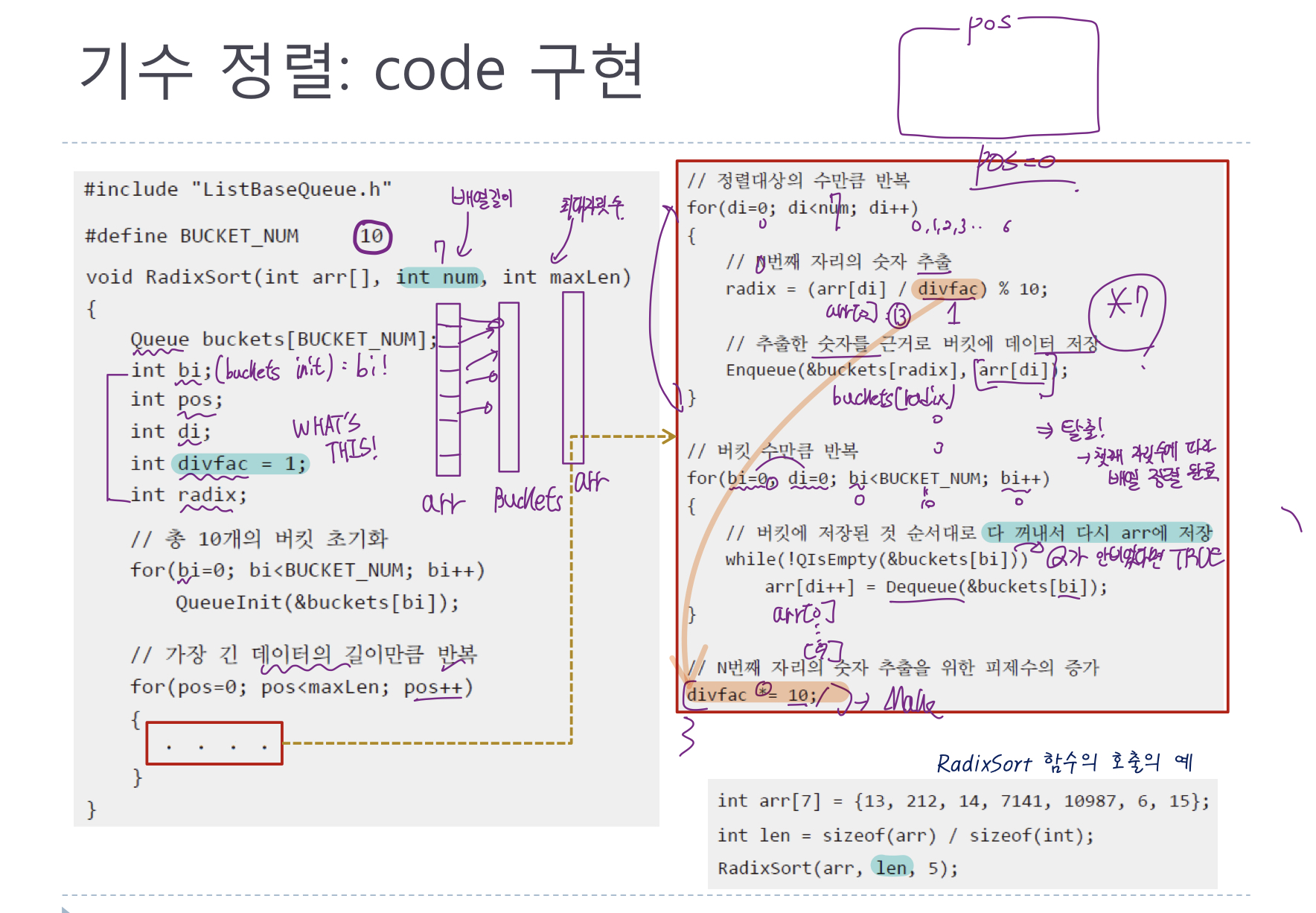
그림이 다소.. 난잡하니 내가 이해한 방식대로 추가적인 텍스트 설명을 하겠다.
우선 bi,pos,di,divfac,radix라는 변수들을 정의해준다!
이변수들의 정확한 의미는... 잘 모르겠다..
그러고 bi를 이용하여 for문에서 버켓들을 초기화해준다.
이제 !
데이터를 배열에서 뽑아내서 양동이에 넣고 양동이에서 다시꺼내는 for문을 작성해야한다.
첫번째 for문은 가장 긴 데이터 길이 만큼 반복한다!
즉 !
이 for문의 처음 실행은 첫째 자릿수를 비교정렬하고
두번째 실행은 두번째 자릿수!.. 마지막자릿수 까지 비교정렬하는 이 for문이 제일큰 포문이다!
이제 이 안에 정렬대상의 수만큼
즉! 배열의 길이 만큼 각 배열의 요소들의 값들을 비교하며 양동이에 넣어줘야한다!
이떄 divfac 를 사용하여 나누는데 이 divfac는 가장 큰 for문을 돌때마다 10씩 곱해줘야한다!
그래야지 첫 for문이 처음은 첫째자리 두번째는 둘째자리가 될테니 말이다!
이렇게 버킷에 저장한 후 !
이제는 버킷에서 빼줘야한다
다시 for문을 작성하여 버킷이 비기전까지 버킷안에 든 모든 데이터들을 arr에 다시 저장한다!
이것을 ! 가장 긴 데이터의 길이까지 반복한다!!!
캬!!! 오졌다!
예술적인 알고리즘이다!
이제
기수정렬 : 성능평가
를 해보자 .
기수연산은 코드에서 보이듯 비교연산이 핵심이 아니라
삽입과 추출이 핵심이다.
따라서 시간 복잡도는 삽입과 추출의 빈도수를 대상으로 결정해야한다.
for(pos=0;pos<maxLen;pos++)
{
//정렬대상의 수만큼 버킷에 데이터 삽입
for(di=0;di<num;di++)
{
// 버킷으로 데이터 삽진행
}
// 버킷 수만큼 반복
for(bi=0,di=0;bi<BUCKET_NUM;bi++)
{
// 추출 진행
}위에서 버킷을 대상으로 하는 데이터의 삽입과 추출을 한 쌍의 연산으로 묶으면, 이 연산이 수행 되는 횟수는
maxLen * num 이 된다.
정렬 대상의 수가 n이고 최대 길이가 l일때
시간 복잡도에 대한 빅-오는
O(ln)이 된다!
이는 O(n)으로 보아도 된다!
이는 짱짱 퀵 정렬 보다 후우어ㅜ어월 뛰어나다!
물론 적용 가능한 대상이 제한적이라는 단점이 있지만 말이다... 
