보통 자료구조 과목에서는 중위 표기법의 소괄호 출력까지는 신경을 쓰지 않지만....
우리는 한번 구현해보자.

힌트

중위 표기법에는 다음 세가지가 있다

• 3 + 2 * 7
• 3 + ( 2 * 7 )
• ( 3 + ( 2 * 7 ) ) 연산자의 수만큼 소괄호를 구성하는 방법

이 수식 트리에 담긴 수식을 중위 표기법의 수식으로 출력해보자.
그러면 모두 같은 결과가 나온다.
우리는 구현에 앞서 중위 표기법의 출력 방식을 먼저 결정해야한다.
그리고 필자가 추천하는 방식은 마지막 방식이다.

그 이유는 "연산자의 수와 소괄호 한쌍의 수가 일치한다" 이다.
이것이 문제해결의 힌트이다.

이제 소괄호까지 출력되게 만들어보자 !

위의 힌트들을 잘 이해했다면 답은 간단하다!

ExpressionTree.c 에

void ShowInfixTypeExp(BTreeNode * bt)
{
    if(bt == NULL)
        return;
    
    if(bt->left != NULL || bt->right != NULL)
        printf(" ( ");
    ShowInfixTypeExp(bt->left);
    ShowNodeData(bt->data);
    ShowInfixTypeExp(bt->right);
    if(bt->left != NULL || bt->right != NULL)
        printf(" ) ");  
} 

이 코드를 추가해주면 된다.

재귀적인 사고

이것이 트리를 다룰때 제일 중요한 것 같다.
위의 코드또한 그렇다.

코드를 하나 씩 생각해보자.

1. "(" 을 생성한다.

2. 재귀로 Show~(bt->left) 가 들어간다.

3. bt->left로 들어오면
   root : +
   left : 1
   right : 2 이다.
   그렇다면"(" 생성.

4. 다시 재귀로 show~(bt->left)로 들어오면
   root : 1
   left,right : NULL 이다.

5. 이제 root 인 1만 출력한다.
   (왜냐하면 || or 연산자는 유일하게 left,right 가 NULL일때 실행하지 않게 짰기 때문이다.)

현재까지 출력된 문자 ((1

6. 이제 left : 1 재귀가 끝났으니 root : +가 출력된다.
   이제 right : 2의 재귀가 시작된다.

7. 이것또한 5번과 동일하게 출력된다.

8. 그렇다면 이제 root:+ 인 서브트리에서 right의 재귀 까지 끝이 났다.
   그리고 left right가 모두 NULL이 아니니 )을 출력한다.

현재까지 출력된 문자 ( ( 1 + 2 )

9. 이제 root : 인 트리의 left : + 서브트리의 재귀함수가 끝이 났으니 root : 을 출력한다.

10. 이제 right: 7의 재귀가 시작되나..
    7의 left, right = NULL 이다.
    그러므로 7만 출력된다.

11. 이제 트리의 left,root,right 모두 출력이
    끝이 났다.

12. 마찬가지로left,right 가 NULL 이 아니므로 ) 가 하나 출력된다.

13. 이제 함수 끗 !

결론 : ( ( 1 + 2 ) * 7 ) 이다.

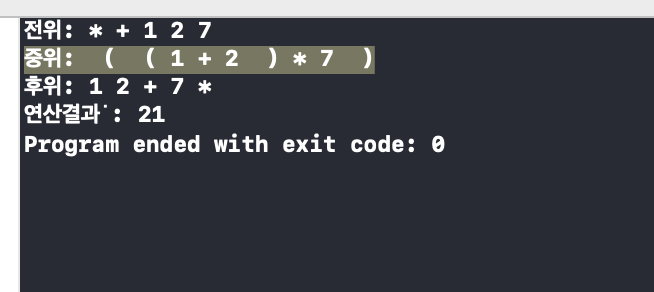
성공적으로 출력됨을 확인 할 수 있다.

무엇보다 트리에서는 진짜로 재귀적인 사고가 중요한것같다.

했던 일을 여러번 반복한다에서 재귀라는 발상을 할 수 있는것같다.

이런걸.. 어떻게 생각해냈을까... 사람들을 참 똑똑하당.....크 흑 이로써 트리는 끝...