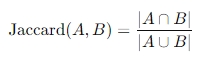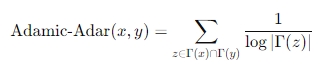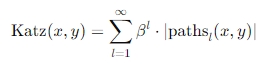많은 지능형 시스템들 (공동저자 추천시스템, 인용 예측, 연구자 그룹 탐지)은 연구자들의 학술적인 성과를 더 높이기 위해 개발되었지만, 학술적인 데이터들을 토대로 연구역량을 강화하는 연구는 아직까지 한계에 부딧히고 있다.
마지막에 연구자들의 연구역량을 평가하는 지표 h-index, g-index, c-index 들은 너무 단순하다.

Figure1을 해석해보자. 그림(a)에서 각 노드는 글을 쓴 연구자를 의미한다. 그림(b)를 보면, 연구자들의 임베딩(embedding)벡터가 시간에 따라 어떻게 변화하는지 분석한 것이다. 해당 연구는 연구자들이 과거에 진행했던 연구기록들간의 유사성을 분석함으로써 롤모델을 발견하였다. 만약 두 연구자가 비슷한 연구이력을 공유하는 동시에 높은 연구 성과를 낸다면, 그 두 연구자의 롤모델이 해당 사람이 될 수 있다는 의미이다.
여기서 임베딩(embedding)의 의미를 살펴보자면, 텍스트, 인용, 공동 연구 네트워크 에서 얻은 정보를 바탕으로 연구자들을 수치적 벡터로 표현하는 방법이다. 이를 통해 복잡한 관계나 특징을 저차원 공간에서 효과적으로 다룰 수 있다.
Trajectory는 궤적을 의미하는데, 연구자들이 시간의 흐름에 따라 변화하는 임베딩 벡터의 위치를 추적하여 연구자의 연구주제, 협업 패턴이나 학문적 영향력의 변화등을 시각화하고 이해할 수 있다.
해당연구의 경우 Weisfeiler-Lehman 재 라벨링 과정은 그래프의 노드들이 가진 초기 라벨 정보를 이웃 노드들의 라벨과 결합하여 점진적으로 업데이트 하는 바복적 알고리즘인데, 이 과정에 변화를 주어 협력 패턴을 의미하는 subgraph들을 추출하였다. 연구자들의 연구 스타일은 굉장히 유동적으로 변화한다. 연구하는 패턴이 일정한 사람이 있는 반면, 주기적으로 연구를 하는 패턴이 변화하는 연구자들도 존재한다.
따라서 해당 논문은 dynamic bibliographic network를 통해 변화하는 연구의 흐름 패턴을 포착하고자 한다. 이렇게 시간에 따라 변화하는 연구 패턴양상을 연구 이력이라고 한다.

5번째 줄을 읽어보면, 예전에는 보통 co-author recommendation을 위해서 Jaccard index, Adamic/Adar index, Katz 라는 link prediction 기법들을 활용했다. 간단하게 세가지 평가 기법들에 대해서 간단히 설명하겠다.
1. Jarccard Index
-정의
- 두 집합간의 유사성을 측정하는 지표로, 두 집합의 교집합 크기를 합집합 크기로 나눈 값이다.
- 그래프에서 두 노드의 이웃집합을 각각 A와 B로보고, 공통 이웃의 비율로 두 노드간의 유사성을 평가하 수 있다.
-특징
- 값의 범위는 0부터 1까지이며, 1에 가까울수록 두 집합이 매우 유사함을 의미한다.
- 단순하면서 직관적이며 링크 예측(Link prediction)이나 추천시스템에서 널리 사용
2. Adamic-Adar Index
-정의
- 두 노드 사이의 연결 가능성을 예측할 때, 공통 이웃의 기여도를 기 이웃의 희소성(연결 정도)를 고려하여 가중치를 부여하는 방식
여기서 Γ(x) 는 노드x의 이웃 집합을 의미한다.
-특징
- 단순히 공통 이웃의 개수를 세는 것과는 달리, 네트워크 내에서 상대적으로 연결이 적은 노드가 공통 이웃으로 등장하면 더 높은 가중치를 부여
- 많은 노드와 연결된 허브 노드보다 상대적으로 특이한 공통 이웃이 두 노드의 유사성을 나타내는데 더 큰 의미 를가진다는 concept에 기반하고 있음
3. Katz index
-정의
- 두 노드 사이의 모든 가능한 경로(path)를 고려하되, 경로의 길이에 따라 가중치를 부여하여 유사성을 평가하는 지표
여기서 β는 감쇠 계수(damping factor)로, 0<β<1의 값을 가지고, 경로의 길이가 길어질수록 기여도가 지수적으로 감소함
-의의
- 경로의 중요도: 짧은 경로가 더 큰 영향을 미치고 긴 경로는 작게 반영됨
- 인접행렬 A를 사용하면, Katz index는 아래와 같이 표현도 가능
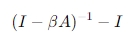
여기서 I는 단위행렬을 의미함.