- 그래프 신경망 (Graph Neural Networks, GNN)
-그래프 컨볼루션 네트워크(GCN): 인접 노드들의 특성을 모아 각 노드의 임베딩을 생성
-그래프 어텐션 네트워크(GAT): 이웃 노드들 간의 중요도를가중치로 반영해 임베딩 형성
-이들 모델은 각 노드의 특성과 주변 구조를 효과적으로 학습하여 두 노드간의 임베딩을 비교하거나 결합해 엣지의 가중치르 예측할 수 있음

- 용어정리
-완전그래프: 그래프 이론에서 모든 정점 쌍 사이에 반드시 엣지가 존재하는 그래프를 의미. 즉, 그래프에 있는 어떤 두 정점을 선택해도 항상 두 정점을 잇는 연결선(엣지)가 존재
예를 들자면, n개의 정점을 가진 완전 그래프 Kn은 모든 정점 쌍이 연결되어 있으므로 엣지의 총개수 공식은 아래와 같다. 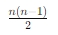
행렬분해기법에서 핵심적인 역할을하는데, 상삼각행렬과 하삼각행렬은 선형대수 및 수치해석에서 매우 유용하게 사용된다. 상삼각행렬과 하삼각행렬은 모두 정방행렬(행과 열의개수가 같은 행렬)로 주 대각선(main diagonal)을 기준으로 특정 부분이 모두 0인 행렬이다.
상삼각행렬(Upper Triangular Matrix)과 하삼각행렬(Lower Triangular Matrix)의 예시는 아래와 같다. 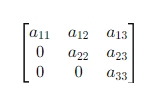
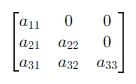
-상삼각행렬은 선형 시스템을 풀 때, 가우스 소거법이나 LU분해 등에서 역순 대임(Back substitution)을 수행한다.
-하삼각행렬은 시스템의 전진 대입(forward substitution)과정에 활용되며 효율적인 계산을 도와준다.
가우스 소거법, LU분해, 전진대입에 대한 자세한 내용은 study에서 자세히 다루도록 하겠다.

간단하게 설명하면 아래와 같다.
- 가우스 소거법 (Gaussian Elimination)
주어진 선형 방정식 시스템의 계수 행렬을 정삼각행렬 형태로 변환하여 해를 구하기 쉽게 만듬
- 각 열에서 0이아닌 원소(피벗)을 선택하는데, 경우에 따라 숫자가 큰 값을 선택하여 수치적 안정성을 높인다.
- 피벗을 이용해 하위 행들에서 해당 열의 원소를 0으로 만드는 일련의 행 연산(row operations)을 수행하는 소거과정
- 상삼각행렬로 변환된 후, 마지막 행부터 시작해 차례대로 미지수를 구하는 역순대입(Back Substitution)을 한다.
- LU 분해 (LU Decomposition)
정방행렬 A를 두개의 삼각행렬인 하삼각행렬 L(lower triangular matrix)와 상삼각행렬 U(Upper triangular matrix)로 분해하는 방법
A = LU
- 전진대입 (Gorward Substitution)
하삼각행렬 L을 계수로 하는 선형시스템 Ly=b의 해를구하는 방법
해당논문은 출점된 지점들에 대한 정보를 기준으로 완전그래프를 구성하여 엣지를 임베딩해 신경망을 학습함으로 엣지 가중치를 예측하는 방안을 제시하였다.
