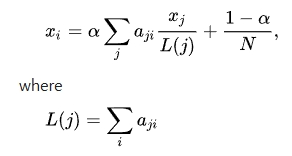사회 네트워크 분석이란 무엇인가?
- 네트워크의 정의
- 라디오나 텔레비전의 방송과 같은 매체에서 각 방송국들을 연결하여 동시에 같은 프로그램을 방송하는 체제 방송망, 중계망
- 랜(LAN)이나 모뎀따위의 통신 설비를 갖춘 컴퓨터를 이용하여 서로 연결시켜 주는 조직이나 체계망, 통신망
- 어떤일이나 문제점을 처리하는 데 각 기관 따위가 긴밀하게 연결되어 조직적이고 효율적으로 움직일 수 있도록 만든 체계
- 네트워크 표현방법
에지 리스트 (Edge list)
Source - 주어 (필수)
Target - 목적어 (필수)
Weight - 빈도 (가중치)
점 = 노드(node): 점/대상/사람
연결선 = 링크(link): 선/연결/관계 ..(ex 친밀도, 증오 등)
네트워크의 기본 개념은 점, 점, 그리고 그 사이의 관계라고 말할 수 있다.
하지만 네트워크에서의 관계는 '방향성' 이라는 개념이 존재한다.
보통 행렬에서 관계가 '있다'와 '없다'를 '1'과 '0'으로 표현한다.
네트워크는 방향성에 따라 다른 가중치를 가질 수 있다.
- 방향성과 가중치가 없는 네트워크 (undirect, weight X)
- 방향성과 가중치가 있는 네트워크 (direct, weight O)
Degree Centrality : Hub = 마당 (연결 중심성)
Betweeness Centrality : Linker = 연결자 (매개 중심성)
Closeness Centrality : Center = 중심자 (근접 중심성)
Eigenvector Centrality : (고유벡터 중심성)
-
Degree: 해당 노드에 몇개의 관계선(링크)이 직접적으로 연결되어 있는지를 나타내느 값, 수치가 높은 노드일수록 해당 노드에 많은 관계가 연결되어있다는 뜻
-
Linker(연결자): 연결해주는 사람(노드)라는 의미를 갖음 대규모 네트워크에서 hub와는 다른 '매개' or '연결'로서의 의미가 발현
일정 규모 이상의 네트워크에서는 그 안에서 다시 소규모의 몇몇 네트워크 들로 다시 분화가 되는 양상을 보이는데, 이러한 분화된 하위 네트워크 군집들을 연결해주는 중요한 노드가 일부 발생한다.
이러한 노드들이 곧 Betweeness centrality(매개 중심성) 수치가 높은 Linker(연결자) 노드로 표현된다.
--> 여기서 중요한 점은 Linker(연결자) 노드들은 단순히 연괼된 관계의 수치(degree)가 높다고 해서 발생하지 않는다는 점이다. -
Closeness Centrality(근접 중심성)이 높은 Center(중심자)는 얼마나 많은 관계가 연결되어 있느냐보다는 전체 네트워크에서 얼마나 중심에 있느냐, 얼마나 핵심적인 위치에 있느냐에 대한 의미가 더 강조된다.
- Eigenvector Centrality (고유벡터 중심성) 은 쉽게말해, '종합점수'의 의미이다. 앞의 연결 중심성, 매개 중심성, 근접 중심성의 개념에 따라 어느정도 수치를 종합적으로 지니고 있는지를 알 수 있는 값이 Eigenvector Centrality(고유벡터 중심성)이다.
--> 그렇다면 여기서 말하는 중심성이란 그렇다면 무슨 의미인가?
그래프이론과 네트워크 분석에서 중심성 지표는 그래프 내의 노드에 네트워크 위치에 해당하는 숫자나 순위를 지정한다 소셜 네트워크에서 가장 영향력이 있는사람, 인터넷이나 도시 네트워크의 주요 인프라 노드, 질병의 슈퍼 스프레더, 뇌 네트워크 식별 등이 있다. 중심성의 개념은 소셜 네트워크 분석에서 처음 개발되었으며, 중심성을 측정하는 데 사용되는 용어들은 인문, 사회학적인 경향을 띄고 있다.
아래는 중심성 계산 공식들을 살펴보겠다.

다음 보이는 그림은 무작위적 기하학적 그래프의 중간 중심성, 근접 중심성, 고유 벡터 중심성, 차수 중심성, 조화 중심성, 카츠 중심성의 예이다.
- 고유벡터 중심성(Eigencentrality) : 네트워크에서 Node의 영향력을 측정하는 방법이다. 높은점수를 받는 노드에 대한 연결이 낮은 점수를 받는 노드에 대한 동일한 연결보다 해당 노드의 점수에 더 많이 반영되며 개념적으로 네트워크의 모든 노드에 상대점수를 반영하게 된다.
Google의 Pagerank와 Katz 중심성은 고유벡터 중심성을 변형한 것이다. 중심성의 개념 또한 여러가지가 있지만, 나는 고유 벡터 중심성, 카츠 중심성, Pagerank 중심성 세가지를 중점적으로 다루어보려고 한다.
인접행렬을 사용하여 고유 벡터 중심성을 찾을 수 있다.
주어진 그래프 G = (V,E) 에 대하여,
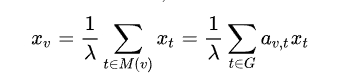
이를 제배열 하면 벡터 표기법으로 고유벡터 방정식을 쓰는것이 가능하다.
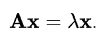

출처: Centrality Degree - Wikipedia
여기서 Perron-Frobenius 정리는 행렬이론에서 Oskar Perron(1907)과 Georg Frobenius(1912)가 증명한 공식으로, 양의 성분을 갖는 실수 정사각 행렬이 가장 큰 크기의 고유한 고유값을 가지고 해당 고유값이 실수라는 점을 명확하게 밝혀내었다.
- Katz 중심성
-차수 중심성의 일반화이다. 차수의 중심성은 직접 이웃의 수를 측정하고, 경로를 통해 연결될 수 있는 모든 노드의 수를 측정하는 반면, 먼 노드의 기여도는 패널티를 준다. 수학적으로 다음과 같이 정의 된다.
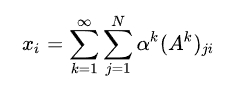
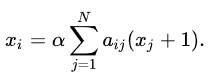
여기서 알파는 감쇠인자로 (0,1)의 범위를 같는다.
- PageRank 중심성
Pagerank의 경우, 고유벡터 중심성과 카츠 중심성과 비교하면, 가장 큰 차이점이 스케일링 계수가 되며, 고유벡터 중심성 간의 또 다른 차이점은 pagerank 벡터가 왼쪽 고유벡터라는 점이다. 여기서 왼쪽 고유벡터란 행렬의 고유값 문제에서 오른쪽 고유벡터와는 반대방향에서 등장하는 개념이다.
Pagerank는 다음 방정식을 만족한다.