트리 순회

서정한·2023년 6월 26일

전위 순회 중위 순회 트리 후위 순회

알고리듬 공부

목록 보기

12/15

트리 순회(tree traversal)

대표적인 3가지 순회법
- 전위(pre-order) 순회
- 중위(in-order) 순회
- 후위(post-order) 순회

중위 순회

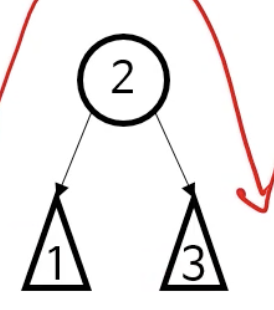
중위 : 왼쪽 하위트리 -> 현재노드 -> 오른쪽 하위 트리
전위 : 현재노드 -> 왼쪽 하위트리 -> 오른쪽 하위 트리
후위 : 왼쪽 하위트리 -> 오른쪽 하위 트리 -> 현재노드
중위 순회 코드

public static void traverseInOrder(Node node) {
	if(node == null) {
    	return;
    }
    traverseInOrder(node.left);
    System.out.println(node.data);
    traverseInOrder(node.right);
}

전위 순회

루트 노드부터 시작
다음 단계를 재귀적으로 실행
1. 내 노드를 먼저 나열
2. 왼쪽 하위트리의 노드를 나열
3. 오른쪽 하위트리의 노드를 나열
이걸 어디다쓰지?
1. 트리의 깊은복사
  - 트리를 만들때 생각해보면 부모를 먼저 나열하고 그 이후에 자식노드를 추가한다. 그래서 전위 순회를 하면 루트노드 -> 왼쪽 노드 -> 오른쪽 노드 순으로 진행되기 때문에 트리를 만드는 과정과 동일하다고 볼 수 있다.
  - 다른 순회로도 복사가 가능하지만 직관적이진 않다.
2. 수식의 전위 표기법
  - 위의 수식은 사람이 보기에 편하지만 컴퓨터가 알아들을 수 있게 다시 변환해줘야한다.
  - 이것을 전위표기법으로 바꾸면?
    - 폴란드 표기법(Polish notation)이라고도 불림.
    - 트리를 전위로 읽으면? => -*A-BC+DE
    - 위 식을 계산하는 방법은? 뒤에서부터 앞으로 읽어나가면서 stack에 넣어 계산함. 계산하는 방법은 연산자가 나오기 전까지 stack에 push하다가 연산자가 나오는순간 두 값을 pop하여 연산한 후 다시 stack에 push한다. 이 과정을 반복하면 계산 끝!
      1. 두 값 push
        
        push E
        
        push D
      2. pop 후 연산 수행
        
        pop D
        
        pop E
        
        push D+E
      3. 두 값 push
        
        push C
        
        push B
      4. pop 후 연산 수행
        
        pop B
        
        pop C
        
        push B-C
      5. 값 push
        
        push A
      6. pop 후 연산 수행
        
        pop A
        
        pop B-C
        
        push A*(B-C)
      7. 두 값 pop 후 연산 수행
        
        pop A*(B-C)
        
        pop D+E
        
        A*(B-C)-(D+E)
      8. 결과 값 반환
    - 위 과정에는 연산자 우선순위 및 괄호 우선순위가 없다. 오로지 읽는 순선대로 진행된다. 따라서 컴퓨터가 계산하기 더 편한 식이된다.