암호학적 해시 알고리듬

• 해시값에서 원본 값을 찾는게 사실상 실행 불가능한 알고리듬
  • 현실적으로 어마어마한 컴퓨팅 파워가 필요해 실행이 불가능에 가깝다는 의미.
  • 일방향 함수(one-way function)
  • 수학적 지식이 많이 요구되는 부분
  • 이미 있는 해시 함수를 주로 사용
• 원본값을 찾으려면 모든 조합을 모두 시도해봐야 함(무차별 대입 공격)
  • 이상적 목표
  • 암호학적 해시 함수로 분류된 것 중 이미 깨진 것들이 있음... ㅠ
• 보안 분야에서 다양한 용도로 사용.

암호학적 해시 알고리듬의 용도 예

• 메세지나 파일의 무결성(integrity) 검사
  • 예: 미러사이트에서 파일 다운로드시 파일 검증
• 디지털 서명 생성 및 검증
• 비밀번호 검증
• 작업 증명(proof-of-work, PoW)
  • 블록체인 등에서 서비스 거부공격(DoS)을 어렵게 만들기 위해
  • 여러 데이터를 넣어보며 해시 값을 찾는 일이 바로 Work의 의미.
• 일반 해시 알고리듬 대신으로 사용가능(단, 일반해시 알고리듬보다 느림)
  

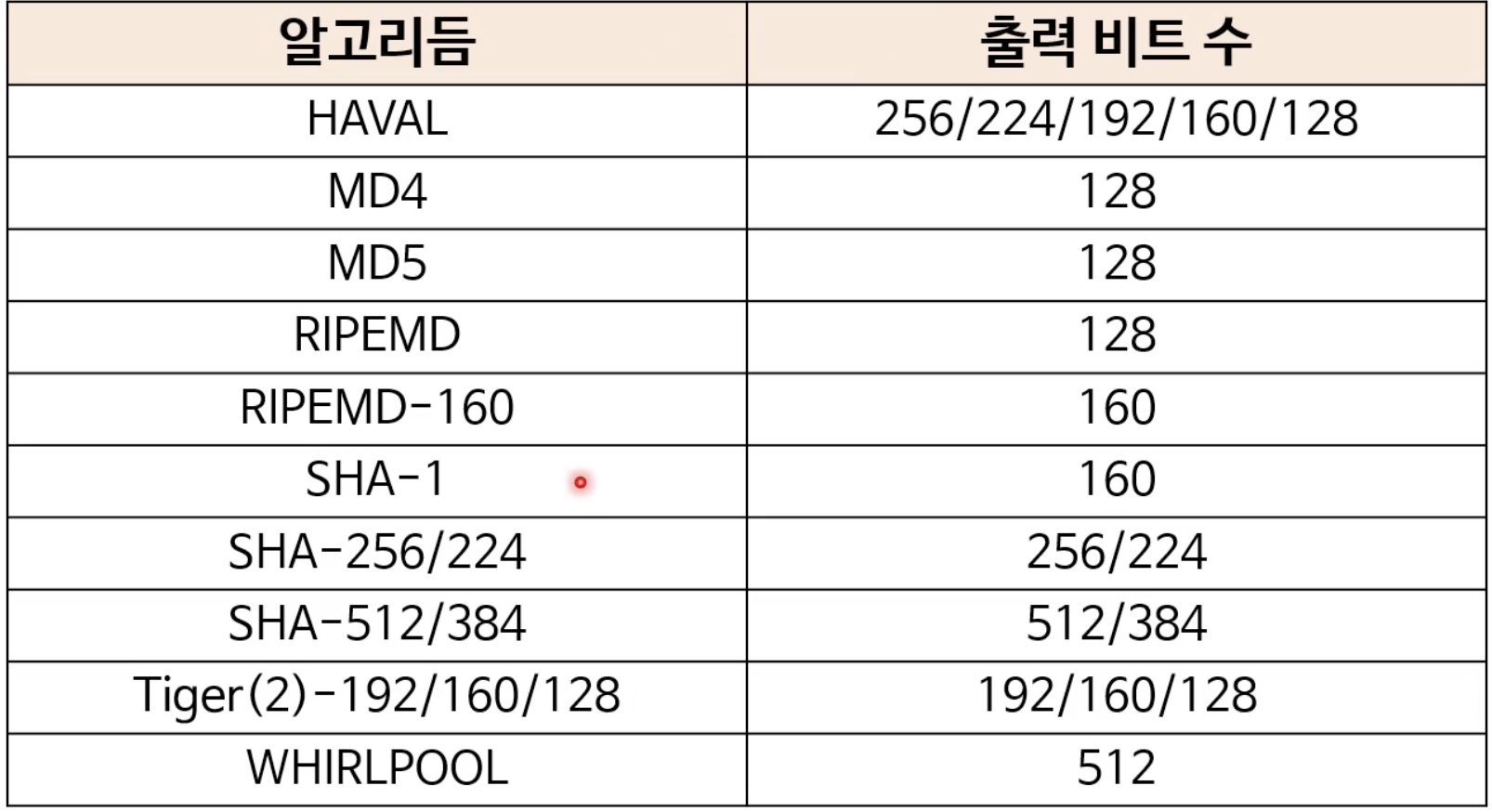
암호학적 해시 알고리듬의 추가 속성

• 역상 저항성(pre-image resistance)
  • 해시값으로부터 원본데이터를 찾기가 어려워야 함.
    • 원본데이터를 같이 저장하지 않는 용도에 적합.
    • 예: 비밀번호 저장.
  • 비보안적 해시함수에서 본 비트패킹은 역상 저항성이 거의 없음.
    • 낮은 역상저항성을 이용하는게 역상 공격(pre-image attack)
    • 무차별 공격으로만 해시값을 찾을 수 있는 것이 이상적!
  • 해시값으로부터 패턴을 보기 어려워야 함.
    • 해시값의 길이가 길수록 좋음.
• 제2 역상 저항성(second pre-image resistance)
  • 똑같은 해시값이 나오는 다른 입력값을 찾기 어려워야 함.
    • 이게 무슨말이냐? 내가 어떤 해시값을 알고 있고 그것에 대응하는 평문을 알고있다고 할 때 이것을 통해 같은 해시값을 찾을 수 있는가? 에 관한 것.
  • 똑같은 해시값이 나오는 다른 입력값을 찾기 어려워야 함.
• 충돌 저항성(collision resistance)
  • 아무 입력값을 넣었을 때 충돌되는 해시 값을 찾을 수 있는가?
  • 해시값이 똑같은 두 입력값을 찾기가 어려워야함.
  • 충돌공격은 역상 공격들 보다 쉬움
    • 이미 MD5와 SHA-1에 대해 실행가능한 충돌 공격이 발견됨
    • MD5는 일반 컴퓨터로 몇초면 충분할 정도...
    • 모든 암호학적 해시 함수는 생일공격(birthday attack)이 가능하기 때문
    • 생일 공격은 무차별 대입 공격보다 빠름(이유는 생일 문제때문)

생일 문제(birthday problem)

• 회사 직원 수는 20명
• 이 중에 생일이 9월 1일인 직원이 있을 확률은?
  
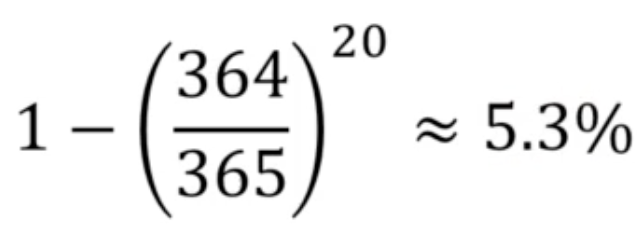
  • 어떤 사람의 생일이 9월 1일이 아닐 경우? 거기에 직원이 20명이므로 모든 직원의 생일이 9월 1일이 아닐경우는 다음과 같다. => (364/365)^20
  • 100%에서 위 경우를 제외하면 어떤 사람의 생일이 9월 1일인 경우만 남게되므로 그림과 같이 계산하면 된다.
• 그냥생일이 겹치는 사람이 있을 확률은? (충돌공격과 비슷)
  • 겹치지 않는 총 경우의 수: P(365, 20) = 365! / (365-20)!
  • 겹칠 확률: 1 - 365! / (365-20)!*365^20 = 약41.1%
• 출력값의 길이가 정해져있기에 생기는 문제임.
  • 모든 암호학적 해시 함수가 생일 공격에 노출되어 있는 이유.
  • 출력값의 길이를 늘리면 그 확률을 줄일 수 있음.
    • 해시값의 크기가 커야 좋은 이유.

본 내용은 Udemy의 알고리듬 및 자료구조(Java)강의를 듣고 정리한 내용입니다.