암호화

서정한·2023년 6월 9일
알고리듬암호화
0

알고리듬 공부

목록 보기
10/15

평문(plaintext)을 암호문(ciphertext)으로 변환하는 것.

  • 암호문도 누군가 훔쳐볼 수 있다. but, 특별한 정보를 아는 사람만 이해할 수 있음.
  • 암호문을 다시 평문으로 변환하는 것 = 복호화(decryption)

해시알고리듬과의 차이점

  • 해시알고리듬은 원문 복구를 막는게 목표.
  • 암호화 알고리듬은 원문 복구를 허용해야 함.

암호화의 역사

  • 고대시절부터 사용한 간단한 형태의 암호화가 있음.
  • 19~20세기에 특히 군용으로 많이 사용
    • 무전으로 보내는 군사정보를 적군이 알면 안됨.
    • 2차세계대전 중 독일군이 사용한 애니그마 기계도 글자 교환 방식
      • 매일 글자 목록이 바뀜
      • 이 규칙을 미리 알고 있지 않으면 24시간마다 규칙을 찾아내야 함

현대사회에서의 암호화

  • 온라인을 사용하여 데이터를 주고받는일이 많아짐.
  • 온라인에 저장된 정보가 너무 많음(특히 개인정보!!)
  • 컴퓨터 성능향상으로 컴퓨터 성능으로 사실상 깰 수 없는 암호화 기법이 필요함.

정수론(number theory)

  • 정수의 성질에 대해 연구하는 학문
  • 수학을 사랑하는 사람들이 매~우 좋아하는 학문
  • 2진수로 표현된 데이터를 암호화하려다보니 갑자기 주목받음.
    • 결국 2진수도 정수이기 때문
  • 특히 소수에 관련된 정수론적 알고리듬이 많은 주목을 받음
    • 암호문의 패턴을 들키지 않으려면 겹치지 않는 수가 필요
    • 소수는 자연에서 가장 겹치지 않는 수

암호학에서 사용하는 정수

  • 매우 큰 정수
    • 32비트보다 더 큰 수를 사용함.
    • 32비트 범위안에 있는 소수는 오직 203,280,220개 뿐
  • 입력크기 N
    • 보통 배열 속의 요소수를 의미
    • 암호학에서 사용하는 정수에서는 비트 수를 의미
  • 곱셈, 나눗셈, 나머지 연산의 시간 복잡도
    • 보통 정수는 O(1)
    • 암호학에서 사용하는 정수는 비트수에 비례

현대 암호화 알고리듬 두 종류

  1. 대칭 키 암호화(symmetric-key encryption)
  • 암호화/복호화에 동일한 키를 사용
  1. 비대칭 키 암호화(asymmetric-key encryption)
  • 공개 키 암호화(public-key-encryption)라고도 함
  • 암호화와 복호화에 사용하는 키가 다름

대칭 키 암호화

  • 암호화/복호화에 동일한 키를 사용
  • 이 키는 메시지 송신자, 수신자가 공유하는 비밀
    • 수신자가 이미 그 키를 가지고 있어야 복호화 가능
  • 송신자가 수신자에게 비밀스럽게 키를 알려줄 방법이 필요
    • 대칭키 암호화의 가장 큰 단점.

스트림 암호 vs 블록 암호

  • 스트림 암호(stream cihper)
    • 한번에 1바이트씩 받아 암호화를 진행
    • 안전하려면 각 바이트에 적용하는 키가 달라야 함.
      • 보통 seed 값을 설정하고 난수로 생성
    • 블록 암호보다 설정이 복잡하나 속도가 빠름
  • 블록 암호(block cipher)
    • 정해진 블록크기(64비트 이상)만큼의 바이트를 한번에 암호화
    • 각 블록에 사용하는 키가 동일함
    • 스트림 암호보다 설정이 간단하나 속도가 느림
  • 효과는 둘다 좋다고 알려져 있음

대칭키의 예

  • Wi-Fi 비밀번호도 일종의 대칭 키
  • WPA2-Personal 작동방식
    • 스마트폰이 처음 공유기 접속시 교환하는 어떤 값과 비밀번호를 합쳐 키 생성
    • 그 키를 이용하여 메세지 암호화 및 복호화
    • but, 해커가 둘 사이 모든 트래픽을 캡처한다면 읽기 가능

대칭키 알고리듬 목록

  • DES
  • IDEA
  • Blowfish
  • AES
  • RC4
  • RC5
  • RC6
  • 등...

AES(Advanced Enctryption Standard)

  • NSA에서 일급비밀 용으로 승인한 유일한 공개 암호화 알고리듬
  • 현재 가장 널리 사용되는 대칭 키 알고리듬
  • 블록 크기: 128비트
  • 키 길이: 128, 192 256비트
  • 키 길이에 따라 평문을 암호문으로 변환하는 라운드수가 다름
    • 128비트: 10라운드
    • 192비트: 12라운드
    • 256비트: 14라운드

AES의 블록

  • AES는 한번에 16바이트씩 읽어서 암호화
  • 16바이트를 4X4 행렬로 배치
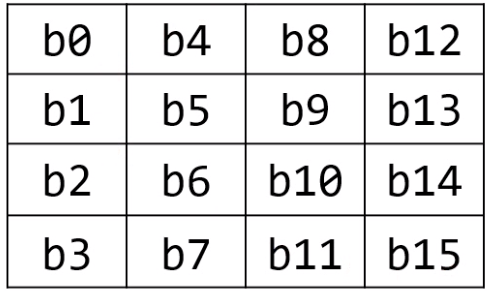
  • 그뒤 여러 처리과정을 통해 암호화 진행

AES알고리듬의 구성

  1. 키 확장
  2. 0라운드
  • 라운드 키 더하기
  1. 9/11/13 라운드
  • 바이트 대체
  • 행 이동
  • 열 섞기
  • 라운드 키 더하기
  1. 최종 라운드(총 라운드 수가 10/12/14가 됨)
  • 바이트 대체
  • 행 이동
  • 라운드 키 더하기

AES알고리듬을 파악하기위해 사용할 데이터

  • 원문: James is the killer!(아스키, 총 20바이트)
  • 첫 블록
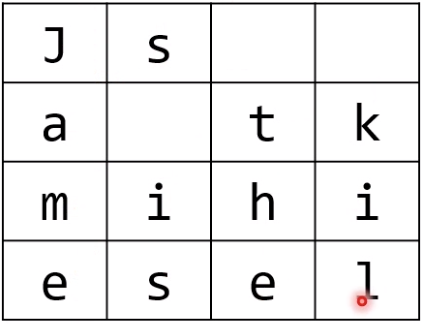
  • 키는 어떤 128비트 정수라 가

1. 키 확장(key expansion)

  • 대칭키로부터 각 라운드에 사용할 여러 키를 생성
    • 이것이 라운드 키
  • 총 라운드 수 + 1개의 라운드 키를 만듦
  • 각 라운드마다 다른 키를 사용하여 키를 찾기 어렵게 만듦

2.a) 0라운드- 라운드 키 더하기

  • 0 라운드 키를 원문에 더함
  • 더한다는 의미는 배타합(xor)
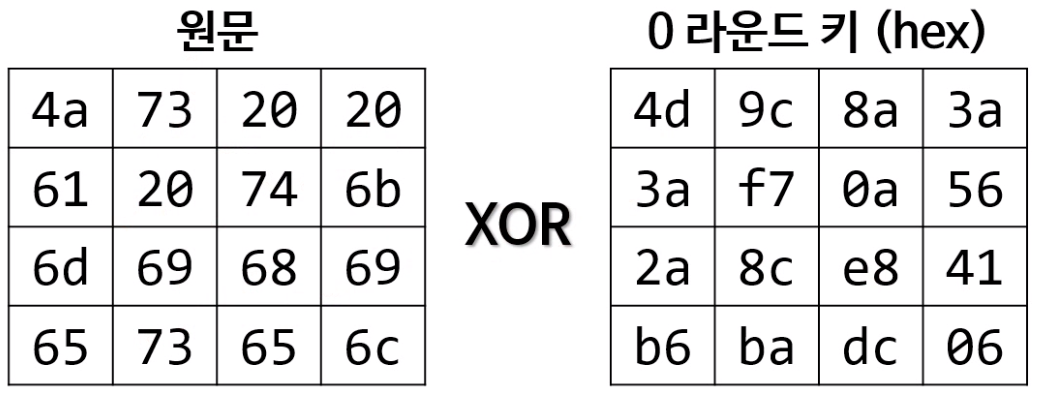
  • 결과
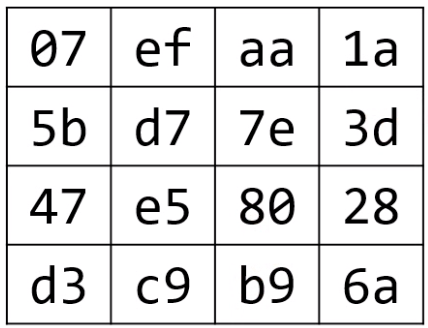
  • 0라운드의 결과는 1라운드의 입력값으로 사용함.

3.a) 여러 라운드- 바이트 대체

  • 각 바이트를 다른바이트로 대체함
    • 바꾸고자하는 바이트에 다른 바이트로 대체하는 것. 이것을 테이블로 만들어 관리하고있음. 그것이 룩업테이블이다.
    • AES S-Box라는 룩업 테이블을 사용
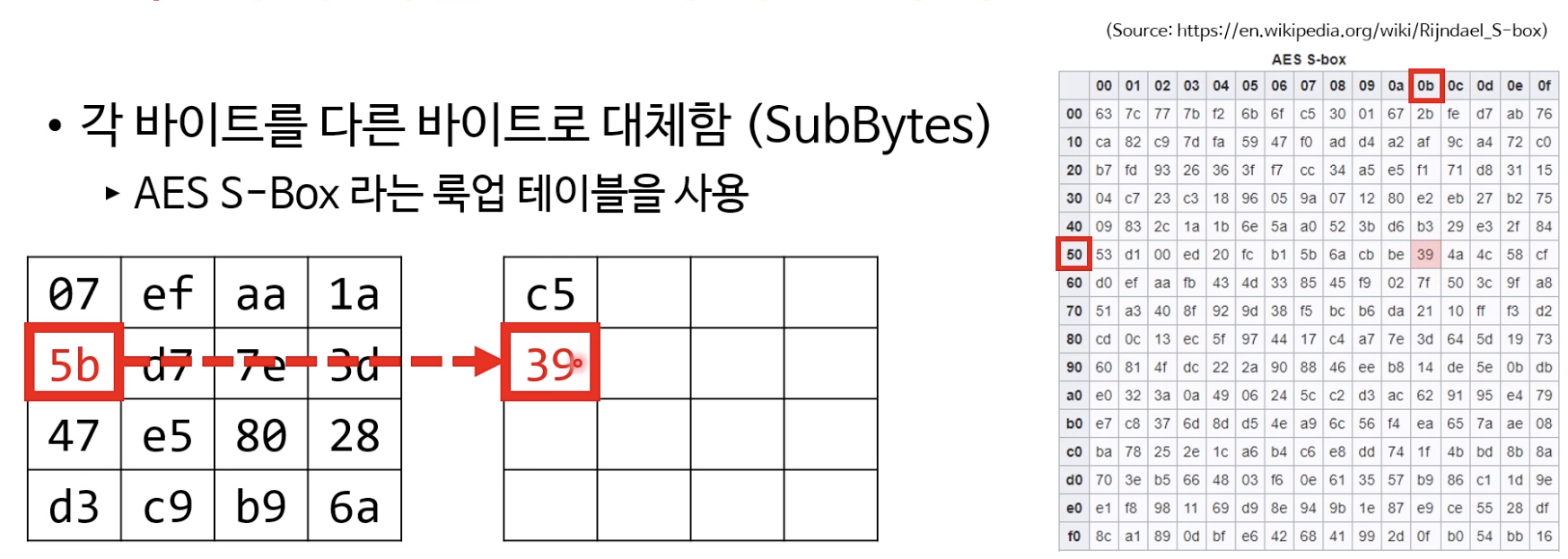
    • 위와 같이 하나씩 테이블에서 찾아 하나씩 다른 바이트로 대체함.
    • 선형적인 변환이 아니라 단순 사칙 또는 비트 연산으로 찾을 수 없음.
      • 선형적인 변환이라는 것은 일정한 공식 혹은 작업을 통해 결과를 내는 것.

3.b) 여러 라운드 - 행 이동

  • 4개의 행을 각각 다르게 왼쪽으로 이동(ShiftRows)
    • 1행: 이동없음
    • 2행: 1 만큼
    • 3행: 2 만큼
    • 4행: 3 만큼

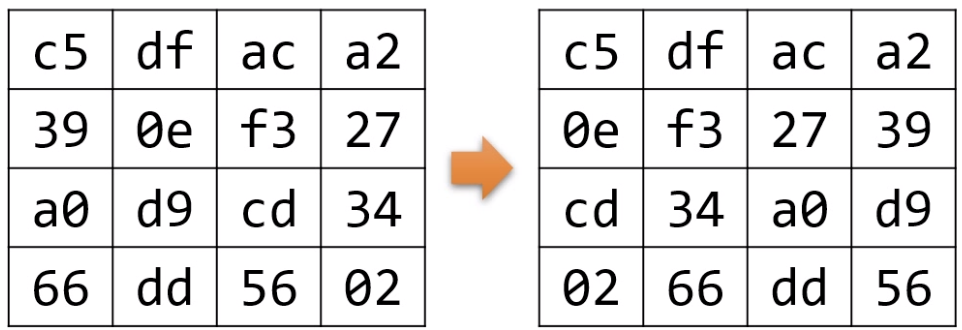
3.c) 여러 라운드 - 열 섞기

  • 각 열에 있는 4바이트를 선형적으로 변환(MixColumns)
    • 행렬 x 백터 곱을 이용(따라서 결과도 4바이트)
  • 일반적인 행렬 곱셈은: C5 X 2 + 0E X 3 + CD X 1 + 02 X 1
  • 위 식에서 덧셈은 XOR연산으로 변경. 곱셈은 특별한 규칙을 적용.
  • 곱셈규칙
    • 1로 곱할때
      • 원래 값을 그대로 유지
    • 2로 곱할 때
      • 원래 값에 2를 곱함(=왼쪽으로 1만큼 비트시프트)
      • 원래 값의 최고비트가 1이었다면 0x1B로 xor
    • 3으로 곱할 때
      • 일반 산술연산: x3 = x2 + x
      • 여기서도 위 규칙을 따름: x3 = x2 xor x
        1. 방금전 봤던 2로곱하는 규칙을 적용한다.
        2. 그 결과에 원래 값을 xor한다.
  • 행렬 x 벡터 곱을 이용(따라서 결과도 4바이트)
    • 일반 곱셈이 아닌 갈루아 필드에서의 곱이라고 함..

3.d) 여러라운드 - 라운드 키 더하기

  • 라운드 키를 더함
  • 3.a) ~ 3.d) 단계를 여러번 반복
    • 대칭키가 128비트면 9라운드
    • 대칭키가 192비트면 11라운드
    • 대칭키가 256비트면 13라운드
  • 다음라운드의 시작점은 이번라운드의 결과값

최종라운드

  1. 바이드 대체
  2. 행 이동
  3. 라운드 키 더하기
  • 열 섞기만 안함.
  • 그 결과가 최종 암호문

비대칭 키 암호화가 필요한 이유

  • 대칭키 암호화는 훌륭한 기법이고 쓸 곳도 많음
    • 하드디스크에 파일을 암호화하여 저장
    • DB에 고객정보 저장
    • 사내 서버간 통신의 암호화
  • 하지만 암호화/복호화에 동일한 키를 사용하는것이 단점.
  • 보안문제없이 쉽게 키를 배포할 수 있는 방법이 필요.

가장 쉽게 키를 배포하는 법

  • 복호화에 사용할 키를 공개하면됨.
  • 그래도 보안이 유지되는 방법이 필요함.(=비대칭 키 암호화)

비대칭 키 암호화 정의

  • 암호화와 복호화에 사용되는 키가 다름
  • 두 키 사이에는 특수한 수학적 관계까 있음.
  • 공개키와 개인키(비밀키)가 있다.

올바른 메세지 암호화

  • 송신자가 수신자의 공개키로 원문 -> 암호문 암호화
    • 공개키로는 암호문 -> 원문 변환 불가
  • 수신자는 자신의 비밀키로 암호문 -> 원문 변환
    • 수신자만 알고 있는 키
    • 수신자만 원문을 볼 수 있음.

비대칭 키 암호화의 두가지 주요 용도

  1. 전송하는 메시지의 암호화
  • 다른사람이 원문을 못보게 숨김
  1. 전자서명(digital signature)
  • 메시지는 누구든 볼 수 있음
  • 메시지 송신자가 올바름을 증명
  • 암호화폐에서 돈을 옮길때도 이 방법을 사용
    • 로그인 시스템이 없기 때문

비대칭 키 암호화를 사용하는곳

  • HTTPS
    • 비대칭 키 암호화와 더불어 대칭 키 암호화도 사용
  • 매신저 앱의 비밀채팅모드
    • 서버도 내 비밀키를 모르는 모드
  • 비트코인 등의 암호화폐 프로토콜
  • Git커밋의 전자서명
    • 예: GitHub에서 지원하는 GPG키

대표적인 비대칭 키 암호화 기법

  • 디피-헬만 키 교환
  • RSA
  • 디지털 서명 알고리듬
  • 타원곡선 DSA

RSA

  • 현재 데이터 전송용으로 매우 널리 쓰임
  • 정수론에 기초함.
  • 공개키/ 비밀키 쌍을 만드는게 매우 쉬움
    • 매우 큰 두 소수를 이용
  • 이 두 키는 특수한 수학적 관계를 가짐
    • 공개 키를 알아도 그로부터 비밀키를 찾기 매우 힘듦
    • 거듭제곱과 나머지 연산만으로 암호화 가능
    • 암호문을 다시 거듭제곱한 뒤, 나머지 연산을 하면 원문이 돌아옴

소수의 특징

  • 소수는 더 이상 인수분해가 안 되는 숫자
    • 1과 소수 그 자체로만 나눠짐
  • 서로 다른 두 소수 p, q를 곱하면 합성수 n이 나옴
  • n의 인수는 p와 q 뿐

RSA가 이용하는 소수의 성질

  • 두 소수를 곱하는 것은 누구나 쉽게 할 수 있는 연산
  • 두 소수를 곱한 합성수에서 그 소수들을 찾는 것은 훨씬 어려움
    • 이렇다할 알고리듬이 없어 모든 조합을 곱해봐야함
    • 예: "8,240,089,796를 인수분해 하시오"(10자리 수)

200자리 숫자에서 두 소수 찾기

  • 시도해야하는 곱셈 수는 루트(10^200) = 10^100 정도.
  • 컴퓨터가 1초에 곱셈을 100만번 할 수 있다면 10^100 / 10^6 = 10^94초가 소요
  • 우주의 나이는 10^18 초가 약간 안됨
  • 우주의 나이보다 10^94 / 10^18 = 10^76배의 시간이 필요하단 뜻
  • 즉, 현재의 컴퓨팅파워로는 불가능한 계산이라는 뜻.

RSA 키 길이와 연산 속도

  • NIST에서 권하는 RSA의 키 길이
    • 2022년: 1024비트
    • 2015년: 2048비트
  • RSA-2048은 1024비트 소수를 2개 사용
    • 2^1024 = 1.798 X 10^308
    • 즉, 308자리 숫자.
  • 혹시라도 컴퓨터 속도가 더 빨라지면 비트 수를 늘리면 됨
    • 이미 4096 비트를 사용하는 사람도 있음.

RSA 공개 키/비밀 키의 기초

  • "비밀 키": 아주 큰 소수 p,q
  • "공개 키": 합성수 n(n = p x q)
  • p,q를 모르면 n으로부터 p,q를 찾기가 매우 힘듦
    • 즉, 공개키로부터 비밀키를 찾기가 매우 힘듦!
    • 이것이 RSA 공개 키/비밀 키 간의 첫번째 특수한 관계
  • 공개 키/비밀 키의 두번째 특수한 관계
    • p,q와 특수한, 그리고 서로간에도 특수한 관계인 e와 d를 찾음
      • e: 공개 키의 두 번째 요소가 됨
      • d: 비밀 키의 두 번째 요소가 됨
  • e와 d는 다음의 관계를 만족해야 함

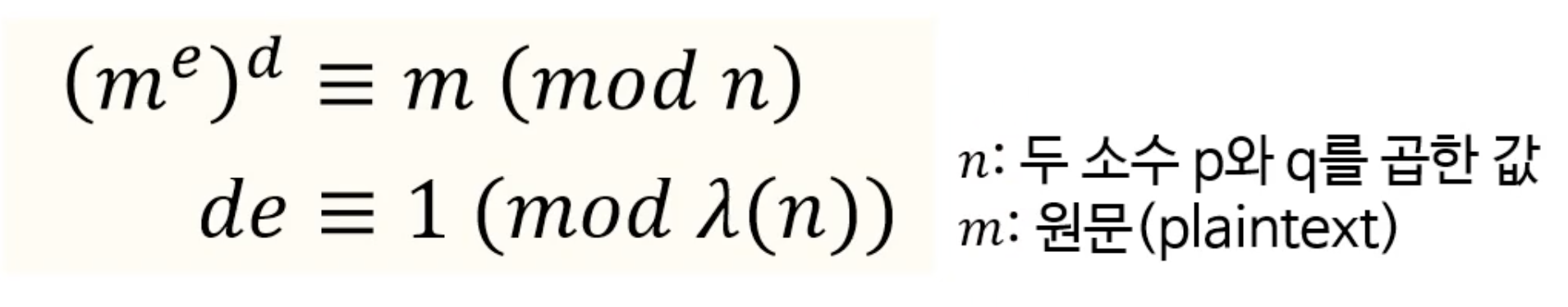
RSA 키 생성

  1. 매우 큰 두 소수 p와 q를 찾는다.
  2. p와q를 곱해 n을 만든다.
  3. p,q와 특수한 수학적 관계인 e를 찾는다.
  4. e와 특수한 수학적 관계인 d를 찾는다.

1. 매우 큰 두 소수 p와 q를 찾는다.

  1. 매우 큰 랜덤 수를 뽑는다.
  2. 그 수가 소수인지 판별한다.
    • 확률적 알고리듬을 통해 꽤 빠르게 할 수 있음(예: 밀러-라빈 소수 판별법)
  3. 소수가 아니라고 판별되면 1번 단계로 돌아간다
  4. 서로 다른 두 소수를 찾을 때까지 이 과정을 반복한다

2. p와q를 곱해 n을 만든다.

  • n = 67 x 53 = 3551

3. p,q와 특수한 수학적 관계인 e를 찾는다.

  1. n의 카마이클 수를 구한다

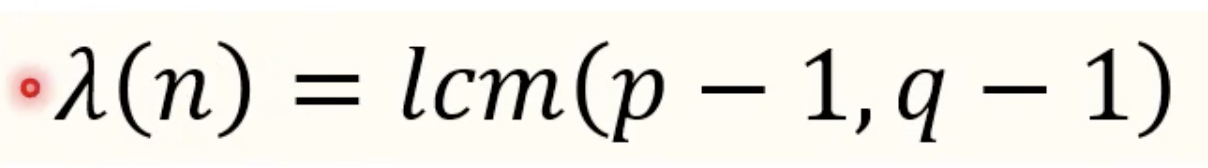
  • 카마이클 수 n은 (p-1, q-1)의 최소공배수와 같다.
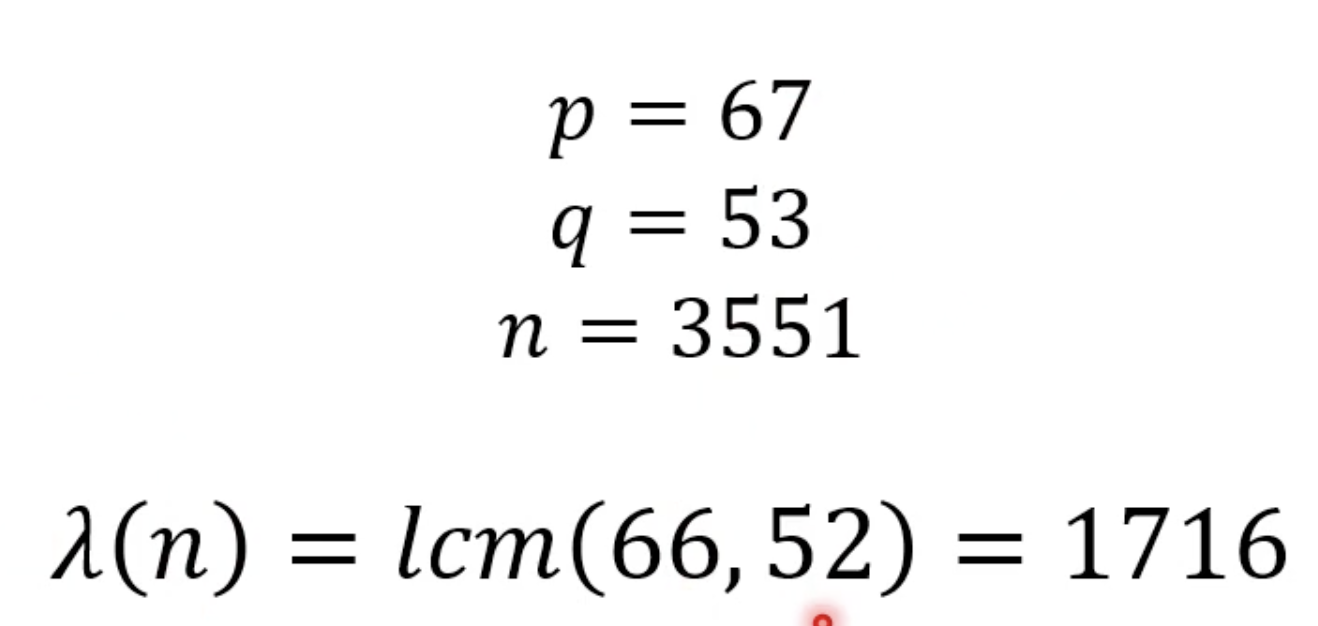
  1. 1 < e < 람다(n)이고 람다(n)과 서로소인 e 값을 찾는다.
  • 서로소: 공약수가 1 뿐인 두 정수
  • e 값은 위 조건을 만족하면 어떤것이든 상관없음

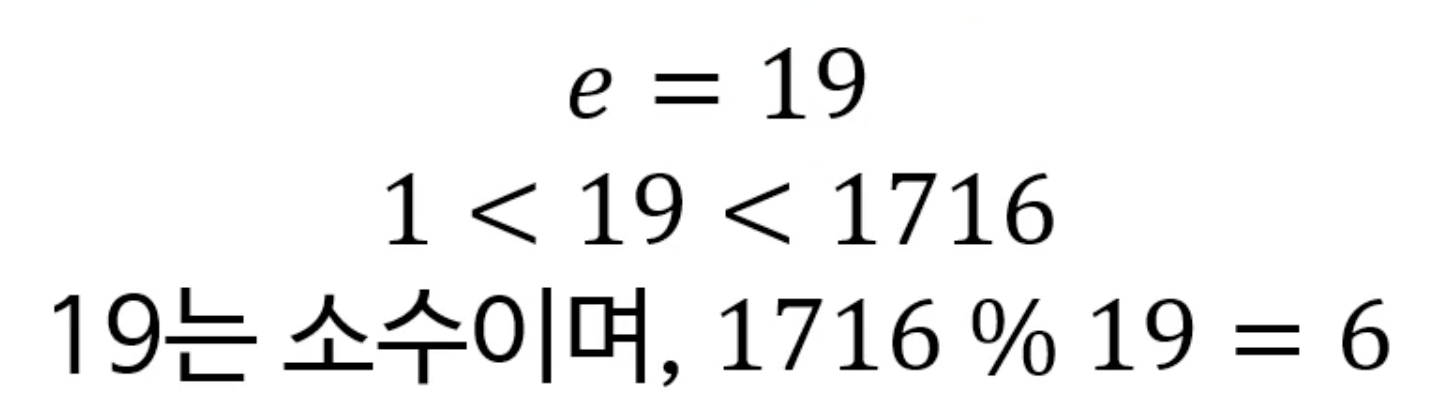
4. e와 특수한 수학적 관계인 d를 찾는다.

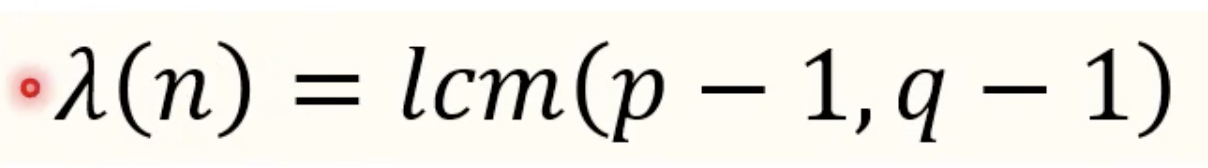
  • 위 조건을 만족하는 d를 찾음
  • 확장 유클리드 호제법을 사용하면 쉽게 찾을 수 있음
  • e와 람다(n)이 서로소이면 반드시 위 조건을 만족하는 d가 존재

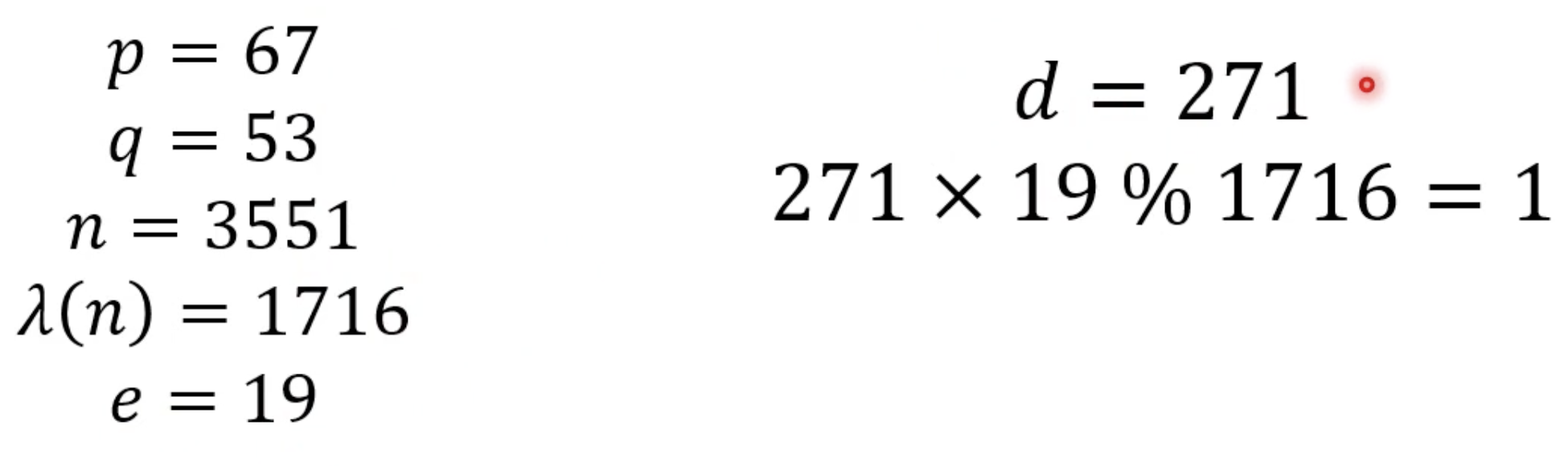
RSA를 이용한 암호화

RSA를 이용한 복호화

이게 왜 되지???

증명

  1. 증명할 관계 찾기
    • c < n일때 n으로 모듈러 연산을해도 c의 값은 변하지 않는다.
    • 합동식의 성질 중 좌항과 우항에 동일한 값으로 거듭제곱할 경우 양 변은 변함없이 동치이다.
    • 이것을 이용해서 암호화 식을 빨간글씨로 바꾼 것.
  2. 복호화 공식이 m을 돌려줌을 증명하고 싶음
  • 합동식의 성질을 이용하여 우리가 증명할 관계를 뽑아낸 것이다.
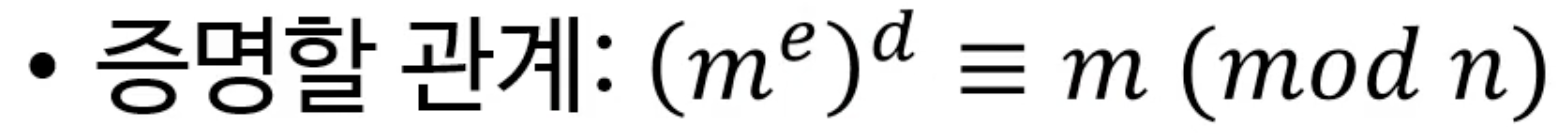
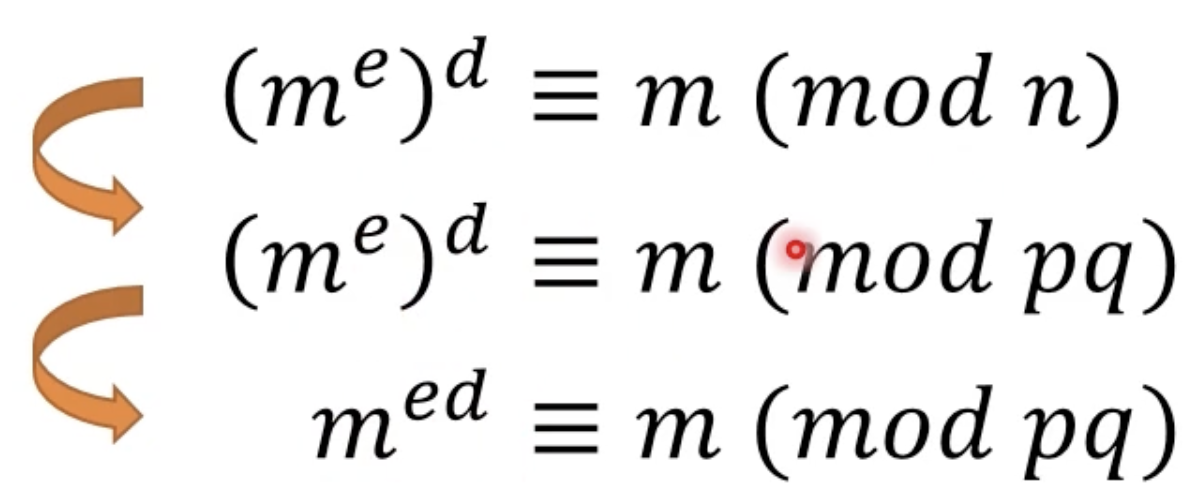
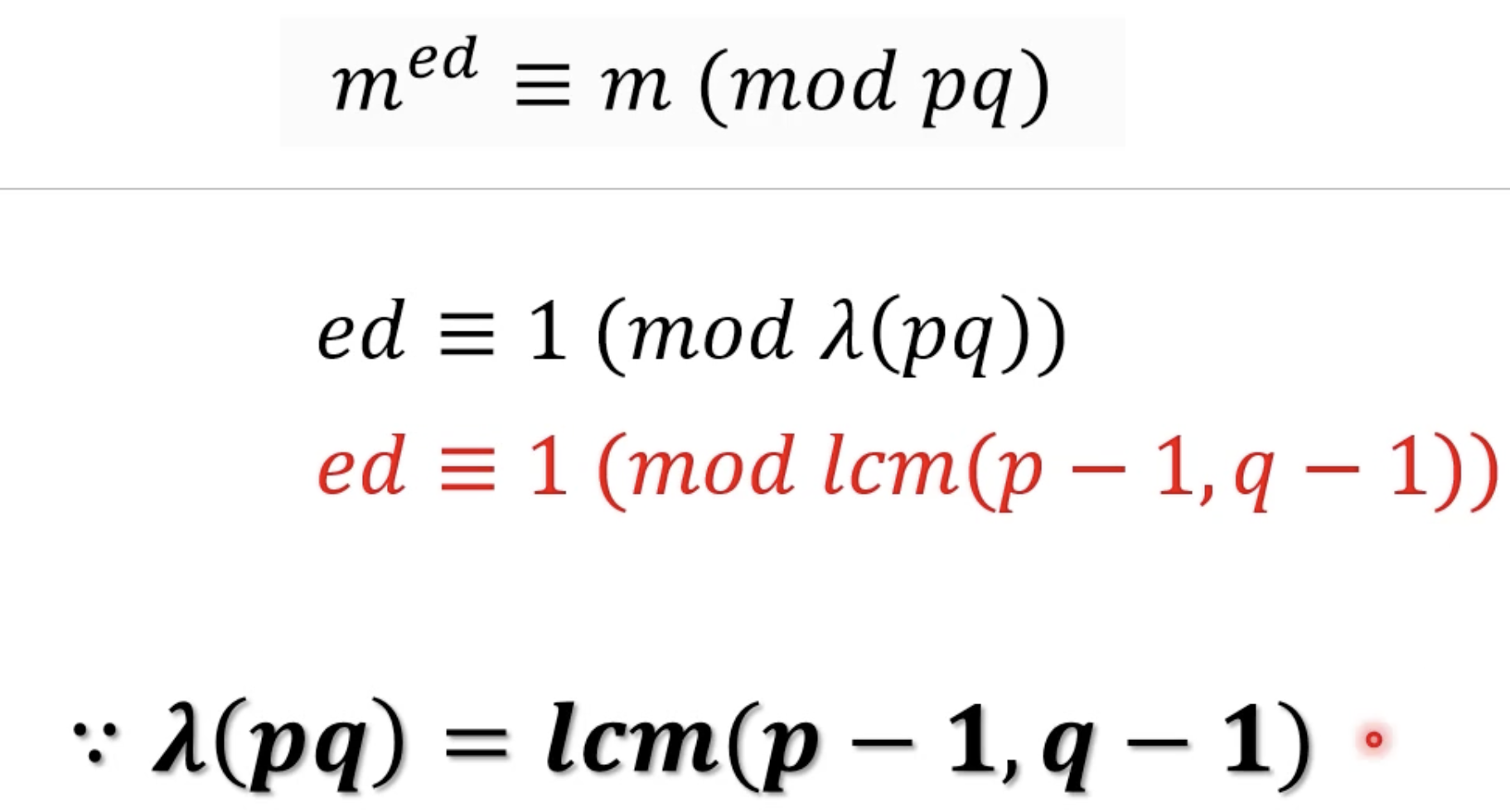
  • 위의 식을 순서대로 따라가면 m의 지수승 ed를 풀어야 한다는것을 알게된다.
  • ed의 우항을 풀어보면 위의 맨 마지막 슬라이드와 같이 나온다.
  • 위 슬라이드와 같이 ed -1 = 최소공배수 (p-1,q-1)의 배수인 어떤 수라는것을 알 수 있다.
  • ed -1 은 (p-1)의 배수, (q-1)의 배수이기도 하다.

  • 위 두식을 각각 증명하면 우리가 최종적으로 증명하고싶은 식을 증명하게되는 샘.
  • 따라서 맨 위의 식과 맨 아래의 식이 동치가 되어버림.
  • 이미 앞에서 증명해버림.

본 내용은 Udemy의 알고리듬 및 자료구조(Java)강의를 듣고 정리한 내용입니다.

profile
서정한
잘부탁드립니다!
이전 포스트

암호학적 해시 알고리듬

다음 포스트

트리

0개의 댓글

관련 채용 정보