트리

개관

• 자료구조이기도하고 트리 알고리듬도 존재함.
• 알고리듬 공부를 했는지에대해 파악할때 트리까지는 잘 물어봄
• 트리는 실무에서 사용할 일이 많음
• 매우 널리 사용하는 자료구조중 하나
• 나무(tree)의 계층적 구조를 표현

트리 관련 용어

• 노드(node): 실제로 저장하는 데이터
• 루트(root): 최상위에 위치한 데이터
  • 시작노드
  • 모든 노드와 직간접적으로 연결됨
• 리프(leaf) 노드: 마지막에 위치한 데이터들
  • 더이상 가지를 치지 않음
• 부모-자식: ㅇ녀결된 노드들 간의 상대적 관계
  • 자식은 없을수도, 많이 있을수도 있음
  • 부모의 size는 언제나 1
  • 조부모/삼촌/형제자매 등도 있음
• 깊이(depth: 노드 -> 루트 경로의 길이
• 높이(height): 노드 -> 리프 경로의 최대 길이
• 하위트리(subtree): 어떤 노드 아래의 모든 것을 포함하는 트리
  • 재귀적: 하위 트리 그 자체가 트리!

트리는 재귀적 자료구조

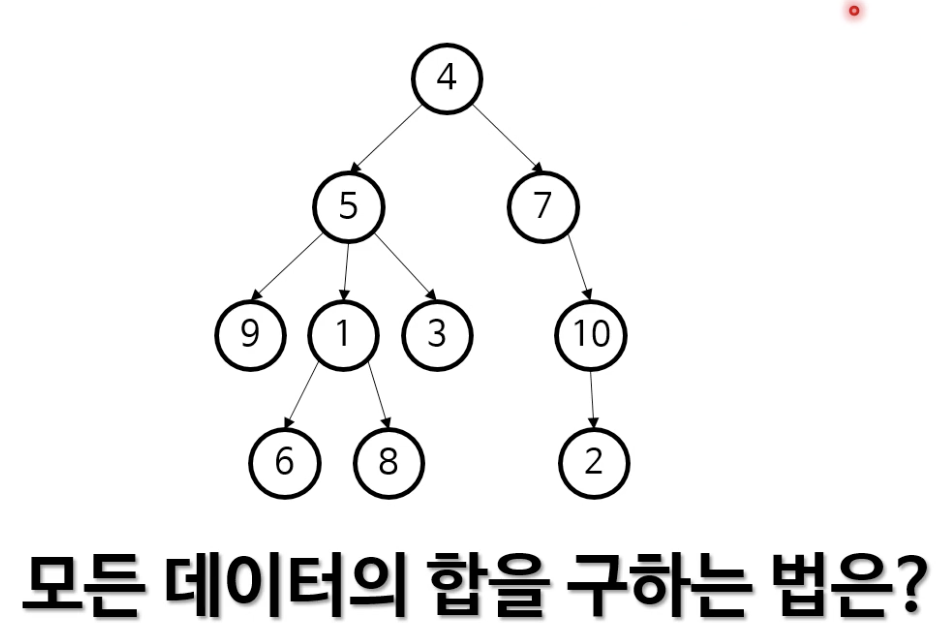
• 재귀적으로 총합구하기- 깊이 0
  • 4 + 5이하 하위트리의 총합 + 7이하 하위 트리의 총합 = 55
    • 9 + 1이하 하위 트리의 총합 + 3 + 10 = 39
      • 1이하 하위 트리의 총합 + 2 = 17
        • 6 + 8 + 1 = 15

트리의 저장법

• 트릐의 속성
  1. 부모와 자식 모두 노드
  2. 부모:자식 = 1:다수
  3. 자식은 언제나 부모로부터 가지를 침
• 따라서 부모가 자식을 참조하는 방식이 가장 직관적

// kotlin
data class Node(val data:Int, val children: ArrayList<Node>)

// java
public class Node {
  public int data;
  public ArrayList<Node> children;
}

• 이게 범용적 트리의 모습입니다.
• 만약 자식이 최대 둘인 트리의 저장법은?(=이진 트리)

public class Node {
  public int data;
  public Node left;
  public Node right;
}

• 만약 자식이 최대 하나인 트리는?(=연결리스트)

public class Node {
  public int data;
  public Node child;
}

트리의 용도

• 계층적 데이터를 표현
  • HTML이나 XML의 문서 개체 모델(DOM)을 표현
  • JSON이나 YAML 처리 시 계층 관계를 표현
  • 프로그래밍 언어를 표현하는 추상 구문 트리(abstract syntax tree)
  • 인간 언어를 표현하는 파싱 트리(parsing tree)
• 검색 트리를 통해 효율적 검색알고리듬 구현 가능
• 그 외 다수

이진탐색트리

• 자식이 최대 둘
  • 왼쪽/오른쪽 자식
• 무언가 계층적(재귀적)으로 이분해 나갈 때 적합
• 이진트리 -> 이진 탐색트리
  • 그 무언가를 이분하는 기준을 만든다면?
    • 그 기준에 따라 특화된 이진 트리를 만들 수 있음
    • 그에 따라 보다 효율적인 알고리듬 고안가능
• 이진트리에 이분하는 규칙을 추가(= 이진탐색트리, BST)
  • 왼쪽 자식은 언제나 부모보다 작다
  • 오른쪽 자신은 언제나 부모 이상
    
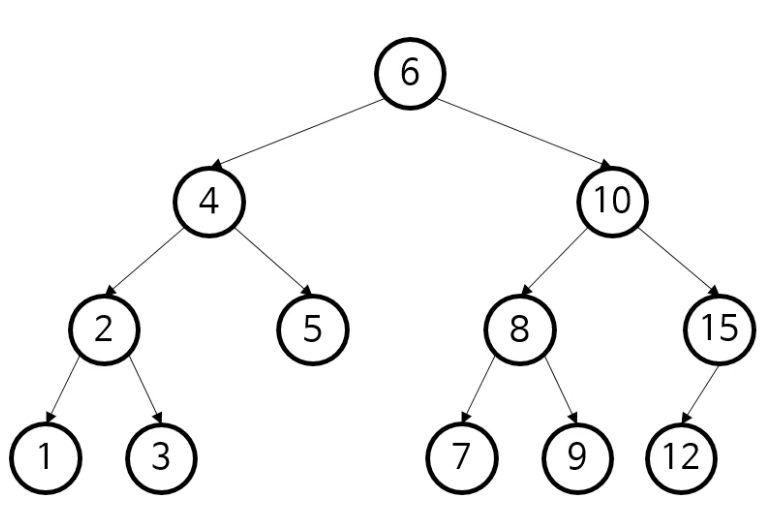
• 정렬된 트리!(재귀적으로 읽는 순서만 지키면)

순서대로 BST읽기

• 루트노드부터 시작
• 다음 단계를 재귀적으로 실행(= 중위 순회법, in-order traversal)
  1. 왼쪽 하위 트리의 노드를 나열
  2. 내 노드를 나열
  3. 오른쪽 하위 트리의 노드를 나열
• 정렬된 트리(= 정렬된 자료구조)
  • 효율적인 알고리듬이 존재함
  • 예: 이진 탐색

정렬된 배열 vs 이진 탐색 트리

• 정렬된 배열
  • 보통 이진탐색전에 정렬을 함.
    • 삽입/삭제 할 때마다 정렬할 수도 있음
  • 새로 추가된 데이터는 비정렬상태
  • 담색시간: O(logn)
  • 삽입/삭제시간: O(n)
  • 매우 간단한 데이터 구조
  • 메모리 한 덩어리
• 이진 탐색 트리
  • 탐색 전 정렬 불필요(이미 이 자체로 정렬된 트리!)
  • 데이터 추가시 정렬된 위치에 추가
  • 탐색시간: O(logn)
  • 평균 삽입/삭제 시간: O(logn)
  • 연결리스트 이상 복잡한 데이터 구조
  • 보통 여러 메모리 덩어리

BST의 복잡도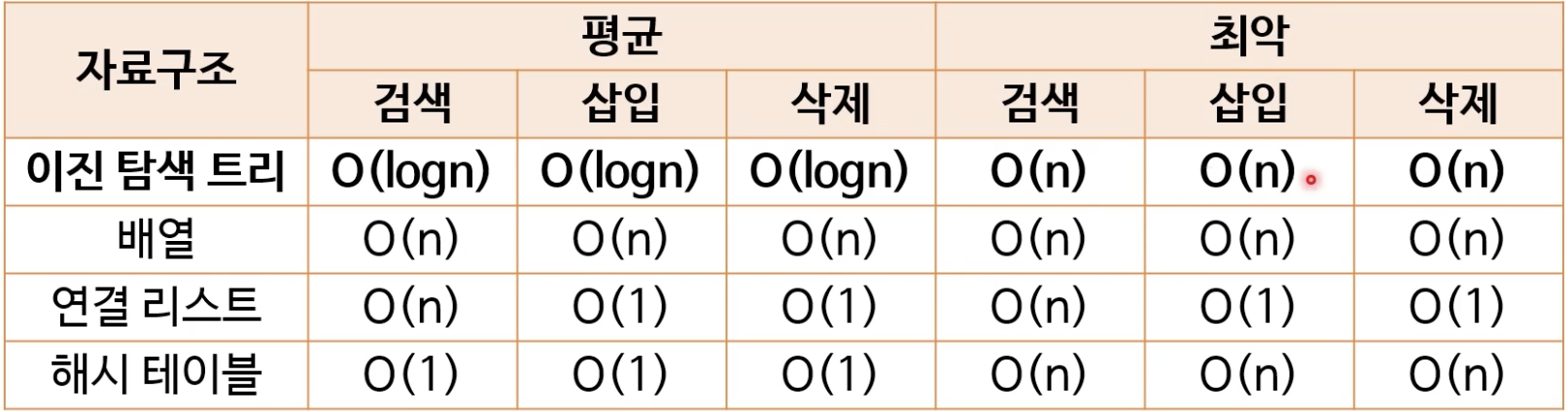

• 공간복잡도: O(n)

BST 탐색

• 기본적으로 이진 탐색과 동일
  • 분할정복(재귀)
• 차이점
  • 각 노드마다 두 하위 트리로 이분됨
• 하위트리로 내려갈때마다
  • 검색 공간이 절반씩줄어듦
  • 평균: O(logn)
  • 최악(줄줄이 자식 하나만 있을 때): O(n)
    • 사실상 연결리스트
• 코드

data class Node(val data:Int?, val left: Node?, val right: Node?)

fun getNodeOrNull(node : Node, data: Int): Node? {
    if(node == null) return null
    
    if(node.data == data) return node
    
    if(data < node.data!!) {
        return getNodeOrNull(node.left!!, data)
    }
    
    return getNodeOrNull(node.right!!, data)
}

BST 삽입

1. 새로운 노드를 받아줄 수 있는 부모 노드를 찾음

• 트리를 내려가는 방법은 탐색과 같음
• 새로운 노드를 받아줄 수 있는 부모란?
  • 오른쪽 하위 트리로 내려가야 하는데 오른쪽 자식이 없는 부모
  • 왼쪽 하위 트리로 내려가야하는데 왼쪽 자식이 없는 부모

2. 그 후 거기에 자식으로 추가
   

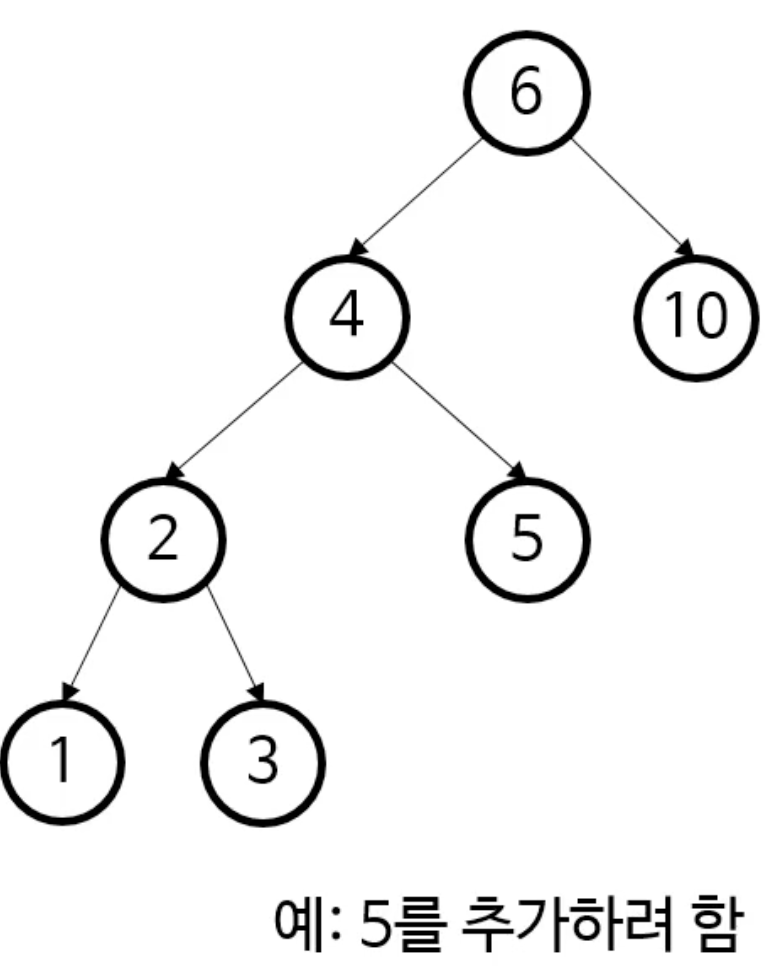
BST삽입은 실제 나무와 비슷

• 이미 자라있는 부분(나뭇가지, 몸통 등..)을 유지
  • 기존 노드 위치를 하나도 바꾸지 않음.
• 새로운 가지를 뻗어나갈 뿐
  • 새로 추가되는 값은 언제나 리프 노드!

BST삭제

• 예시
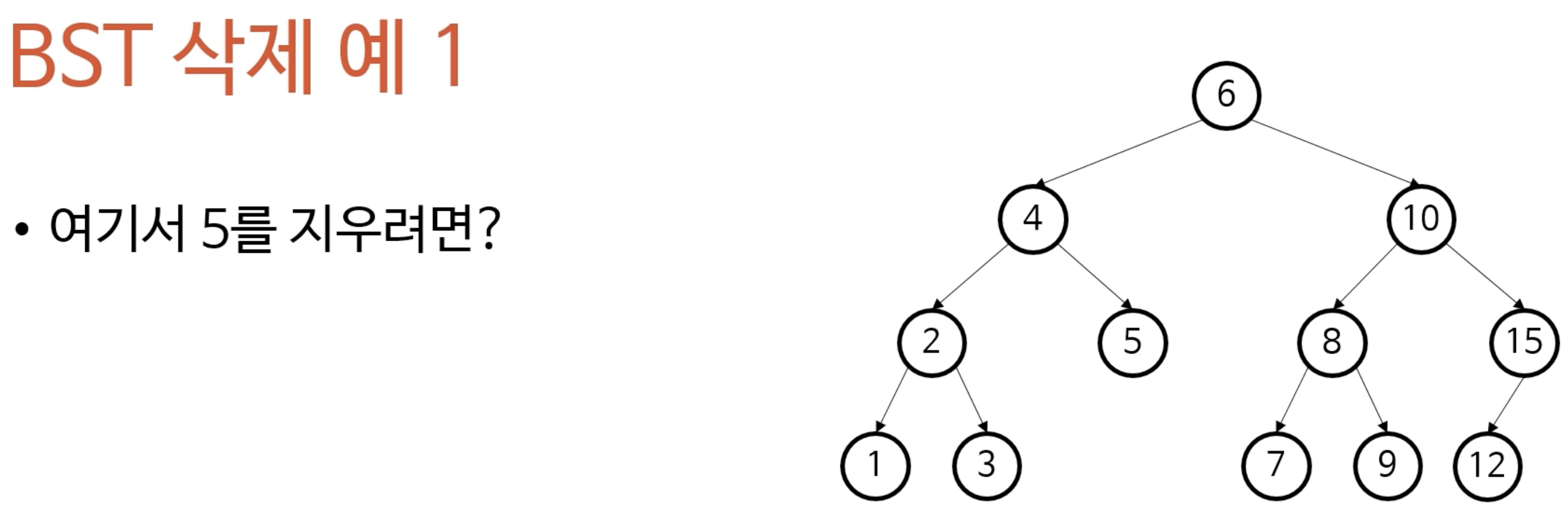
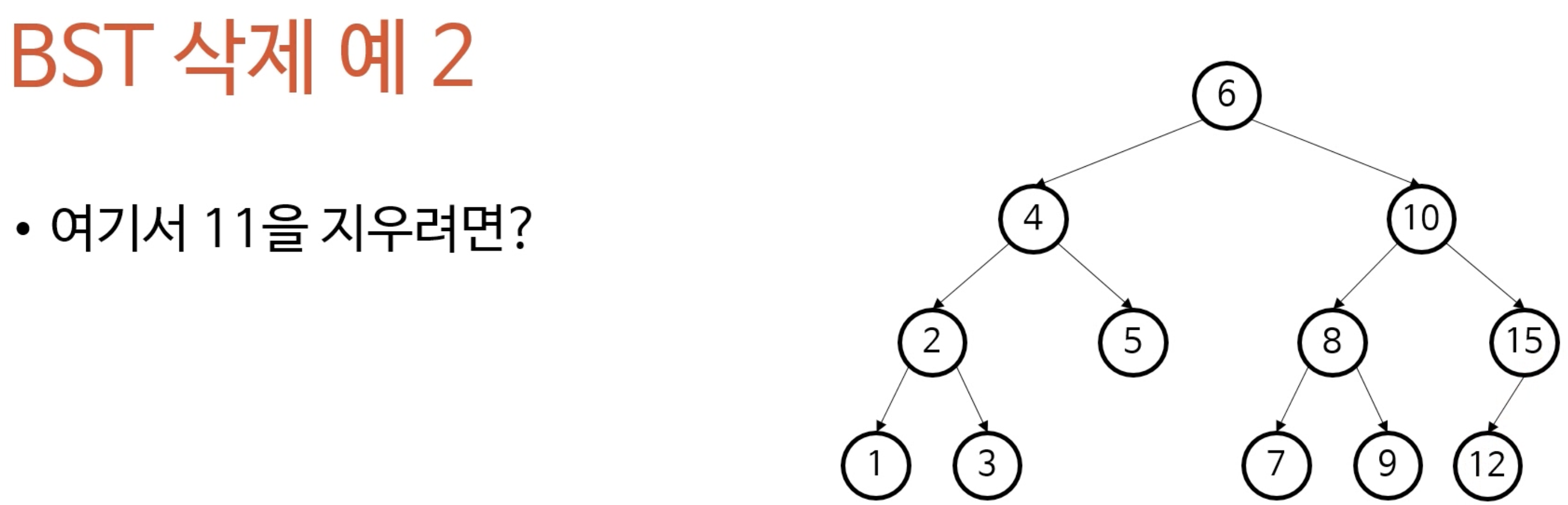
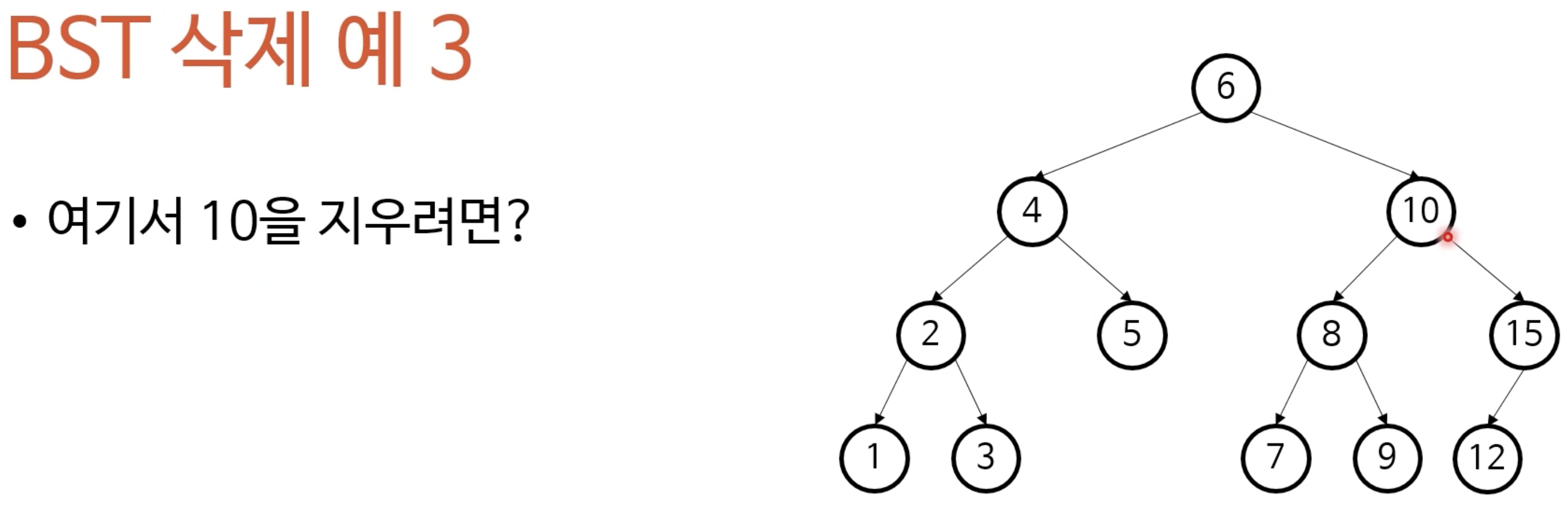
• 10을 지웠을때 문제는 정렬을 다시해야하는데 이 때 순서가 깨져버린다는것이다. 그래서 노드를 삭제한 후 곧바로 자식을 연결하면 안된다.

그래서 삭제는 어떻게...?

• 노드를 삭제한 뒤에도 올바른 BST를 유지하려면 정렬된 배열에서 값을 하나 삭제하듯이 처리하면 된다.
• 트리에서 뭔가를 지울 땐 언제나 리프를 지운다!
• 위 두가지 아이디어를 가지고 삭제처리를해보자..!

BST 삭제 예 3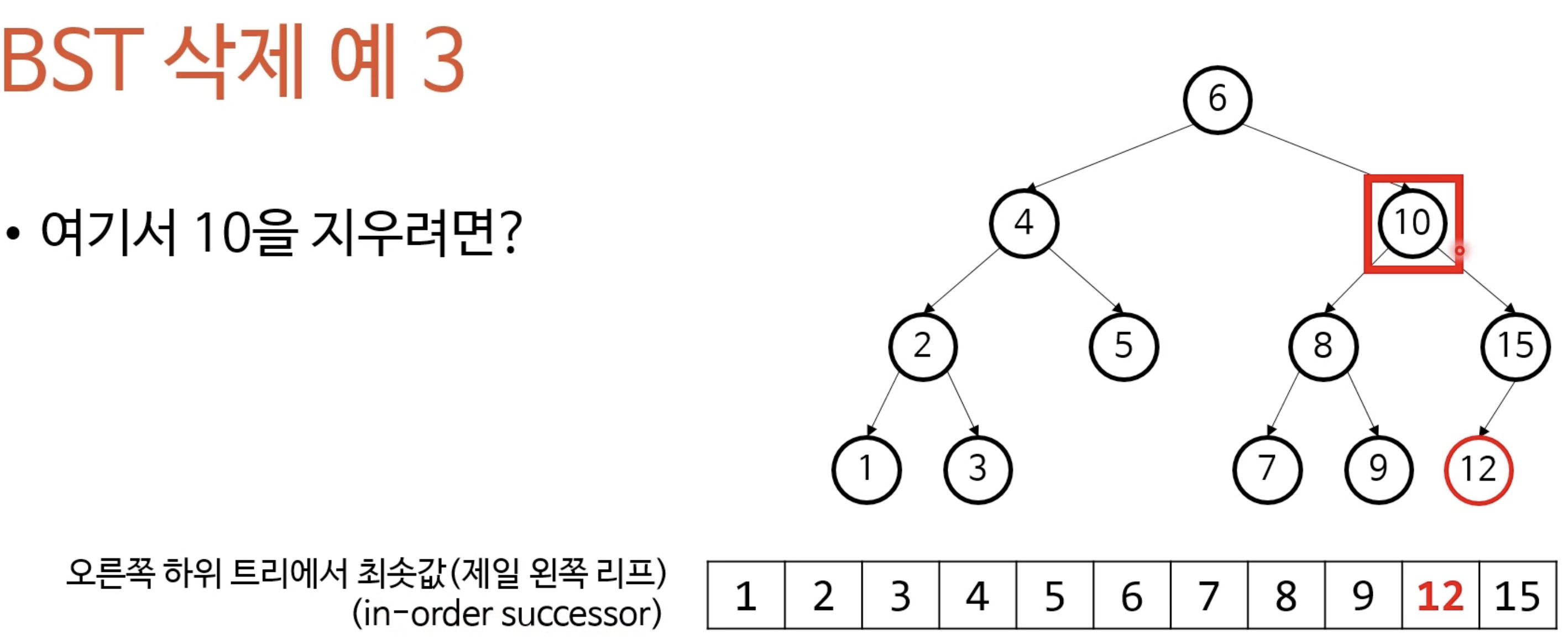

1. 내 바로 뒤를 당겨와 정렬할지?(in-order successor)
2. 내 바로 앞을 당겨와 정렬할지?(in-order predecessor)

BST노드 삭제 전략

1. 지울 값을 가지고있는 노드를 찾음.
2. 그 바로 전 값을 가진 노드를 찾음

• 왼쪽 하위 트리의 제일 오른쪽 리프

3. 두 값을 교환
4. 리프 노드를 삭제

BST삭제 시간복잡도

1. 지울값을 가지고있는 노드를 찾음
2. 그 바로 전 값을 가진 노드를 찾음
3. 두 값ㅇ르 교환
4. 리프노드를 삭제
   => O(logn)

삭제 구현

• 삭제를 구현할 때 고려해야 할 경우는 총 3가지정도된다.
  1. 삭제하려는 노드의 자식노드가 없을 때 : 해당 노드를 삭제하면 끝!
  2. 삭제하려는 노드의 자식이 1개일 때 : 자식노드를 해당노드로 바꾼 후 삭제!
  3. 삭제하려는 노드의 자식이 2개일 때 : 여기서부터가 문제..

그래서 BST 노드 삭제 전략을 위와같이 하는 것!

• 이 모든 경우를 고려한 삭제전략 코드

package com.example.basesyntax

fun main() {
    var rootNode = Node(6)
    val bst = BST()
    bst.insert(rootNode, 4)
    bst.insert(rootNode, 2)
    bst.insert(rootNode, 1)
    bst.insert(rootNode, 3)
    bst.insert(rootNode, 10)
    bst.insert(rootNode, 5)
    bst.insert(rootNode, 8)
    bst.insert(rootNode, 7)
    bst.insert(rootNode, 9)
    bst.insert(rootNode, 15)
    bst.insert(rootNode, 12)
    println(rootNode)
    println("---")
    bst.remove(rootNode, 10)
    println(rootNode)
}

data class Node(var data: Int?, var left: Node? = null, var right : Node? = null)

class BST {
    fun insert(node : Node?, data: Int): Node? {
        if(node == null) {
            return Node(data)
        }

        if(node.data!! > data) {
            node.left = insert(node.left, data)
        }
        else {
            node.right = insert(node.right, data)
        }
        return node
    }
    fun remove(node : Node?, data: Int) : Node? {
        if(node == null) return null
        if(node.data!! > data) {
            node.left = remove(node.left, data)
        }
        else if(node.data!! < data){
            node.right = remove(node.right, data)
        }
        else {
            if(node.right == null) return node.left
            else if(node.left == null) return node.right

            val minValue = findMinValue(node.left)
            node.data = minValue
            node.left = remove(node.left, minValue)
        }
        return node
    }

    fun findMinValue(node: Node?) : Int {
        var currnetValue = node?.data ?: throw NoSuchElementException("BST Element is Empty")
        var currnetNode = node

        while(currnetNode?.right != null) {
            currnetValue = node.right!!.data!!
            currnetNode = node.right
        }
        return currnetValue
    }
}

본 내용은 Udemy의 알고리듬 및 자료구조(Java)강의를 듣고 정리한 내용입니다.