Point Transformer(ICCV, 2021)

PointNet

Point Transformer에 앞서 PointNet를 먼저 간단히 살펴보자면,
PointNet은 아래의 그림과 같이 point cloud를 input으로 받아서 points 자체를 처리하는 네트워크로 구성되어 있다.

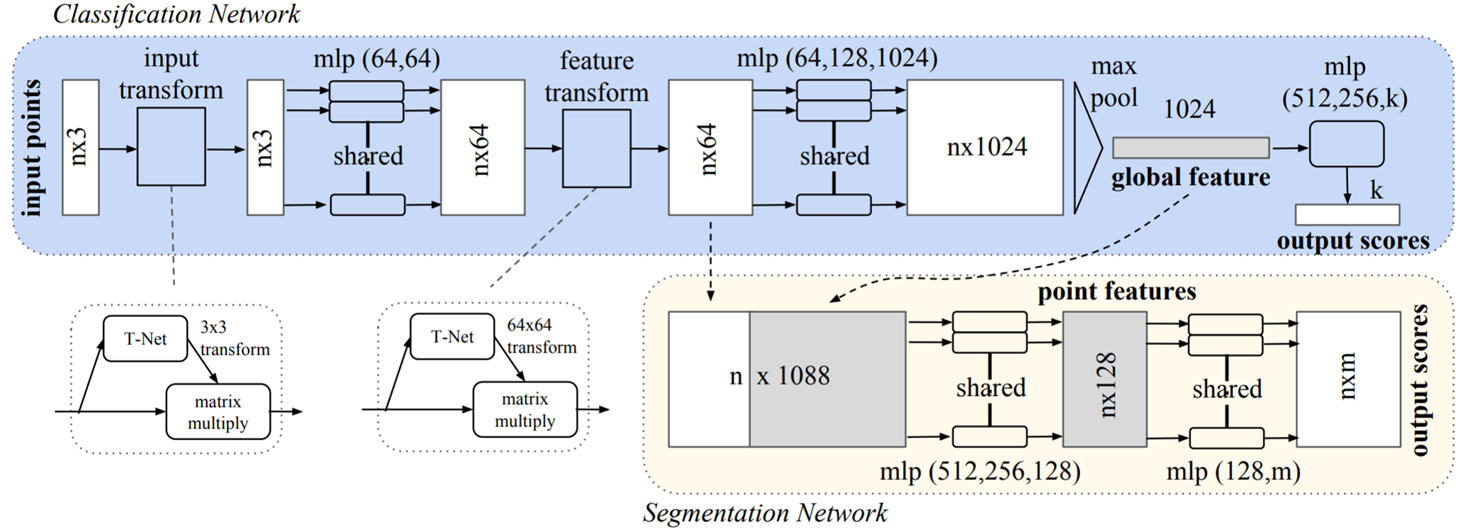
PointNet의 아키텍처는 아래와 같으며, classification을 수행하는 네트워크 구조가 있고 확장 비전으로 segmentation을 수행하는 네트워크 구조가 있다.
먼저 classification Network를 거치는데, input cloud points가 들어오면 transformation을 거치고 mlp shared를 이용하여 feature를 학습한 다음 symmetric function 중 하나인 max pool을 이용하여 global feature를 추출한다.
그리고 segmentation을 위해 학습된 global feature를 segmentation Network를 거쳐서 output scores를 출력하게 된다.

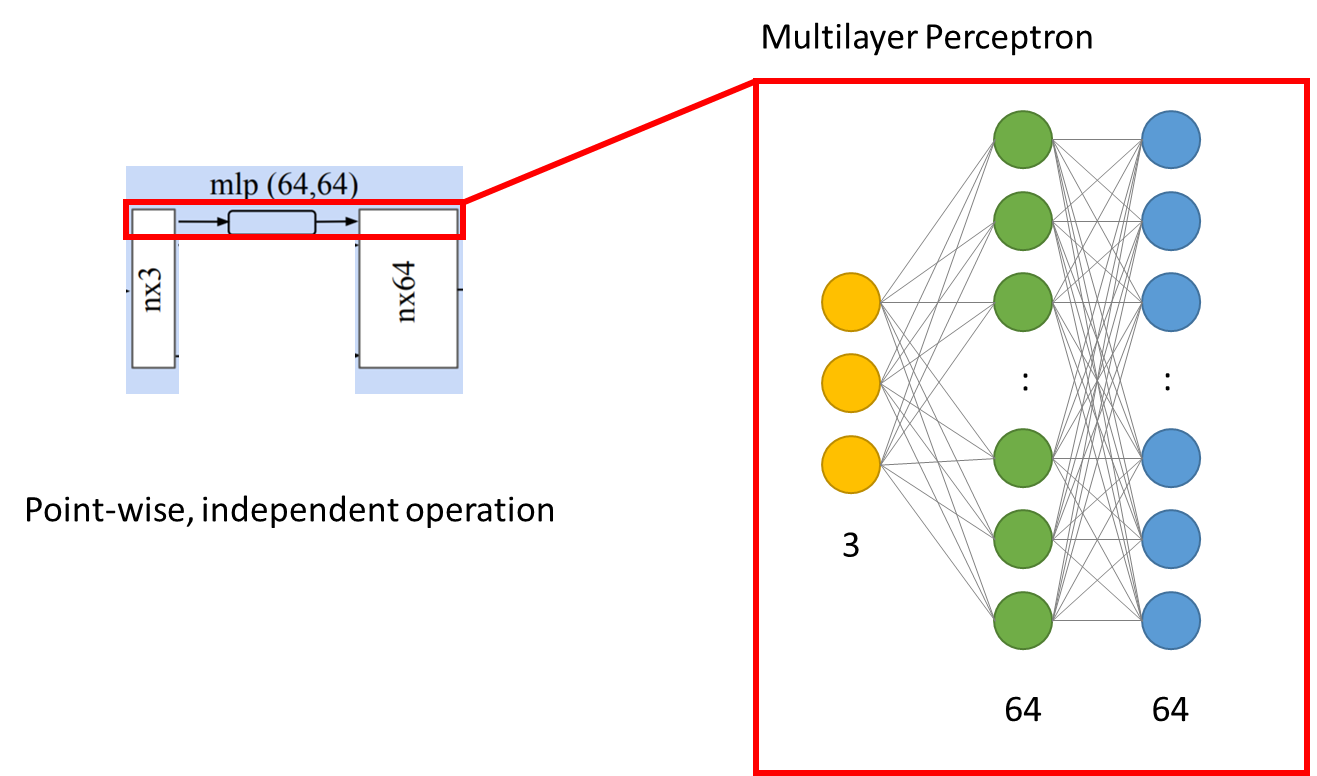
아래는 shared mlp 부분으로 동일한 mlp를 가지고 각각의 points(n*3)를 처리를 한다.

PointNet의 input으로 들어오는 point set은 순서가 존재하지 않는다. 아래와 같이 데이터 형식이 순서가 다르게 들어오더라도 똑같은 기하학적 모형을 가진다. 그래서 permutation inverience의 특성을 만족해야 한다.

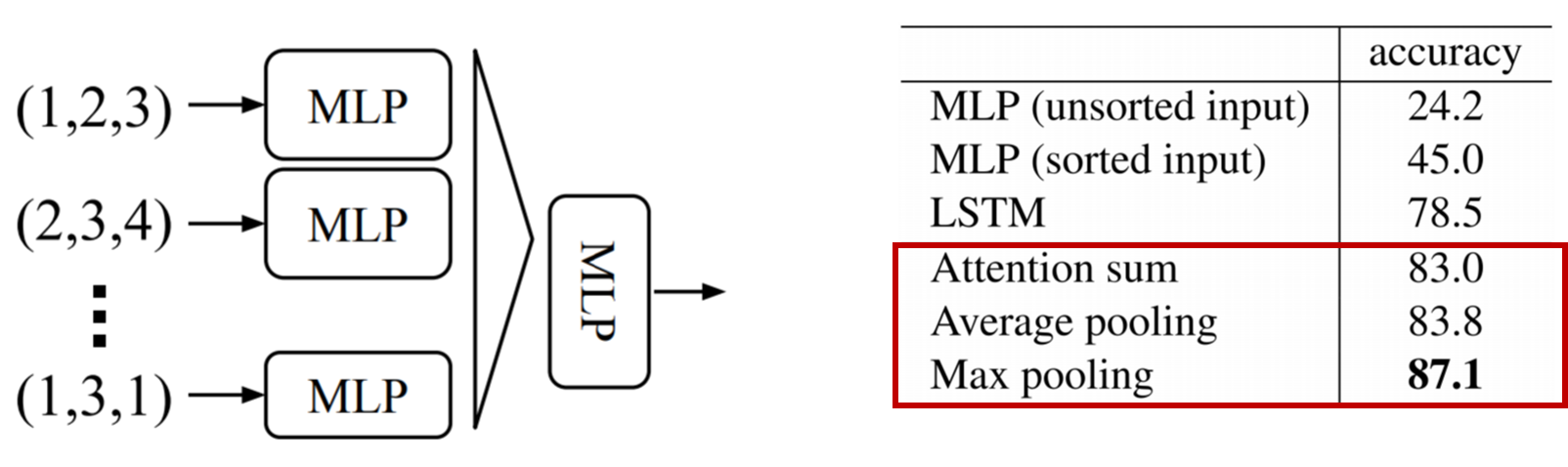
permutation inverience의 특성을 만족하기 위해서는 a symmetric function의 개념이 필요하다. 아래와 그림과 같이, symmetric function은 h라는 function이 각각의 points에 독립적으로 수행되어 output을 내뱉고 output들 모여 g라는 symmetric function을 수행하게 되면 symmetric한 output을 내뱉는다. symmetric이라는 것이 input node들의 순서가 바뀌더라도 g의 output은 바뀌지 않게 된다. 그리고 gamma function를 지나치면 output embedding을 얻게 된다.

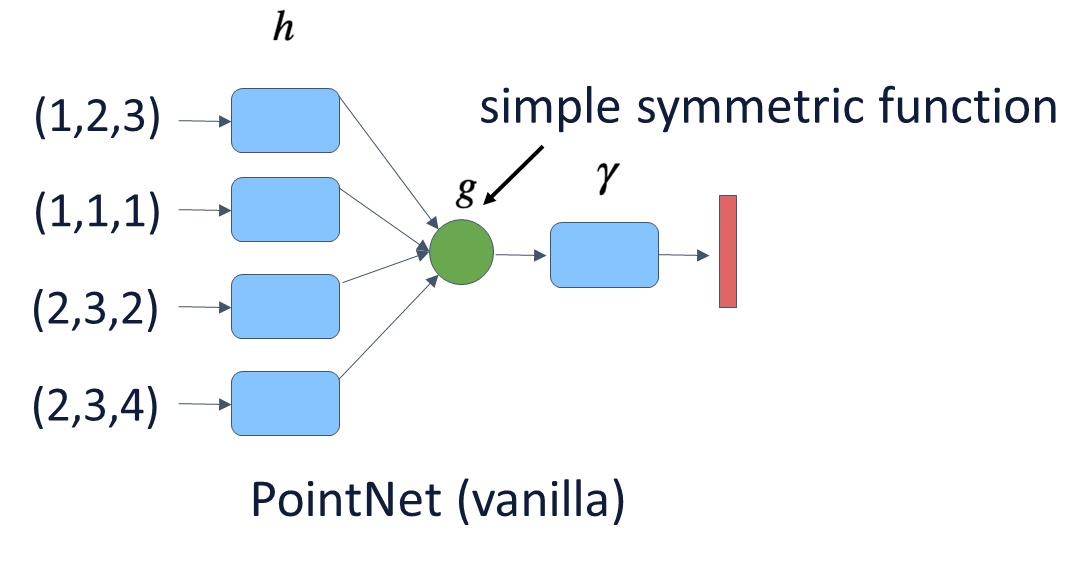
아래의 그림과 같이, 순서가 바뀌어도 같은 output을 내뱉을 수 있는 symmetric function들이다. PointNet과 Point Transformer은 Max Pooling을 사용한다.

2D에서는 계측적인 로컬리티를 이용하는 반면, PointNet은 로컬리티를 사용하지 않기 때문에 3D scene을 처리하는데 비효율적이다. 새로 보지 못한 scene의 설정에 대해서는 일반화하기 어려운 점이 있다.

point clouds에서 locality는 3가지를 말한다.
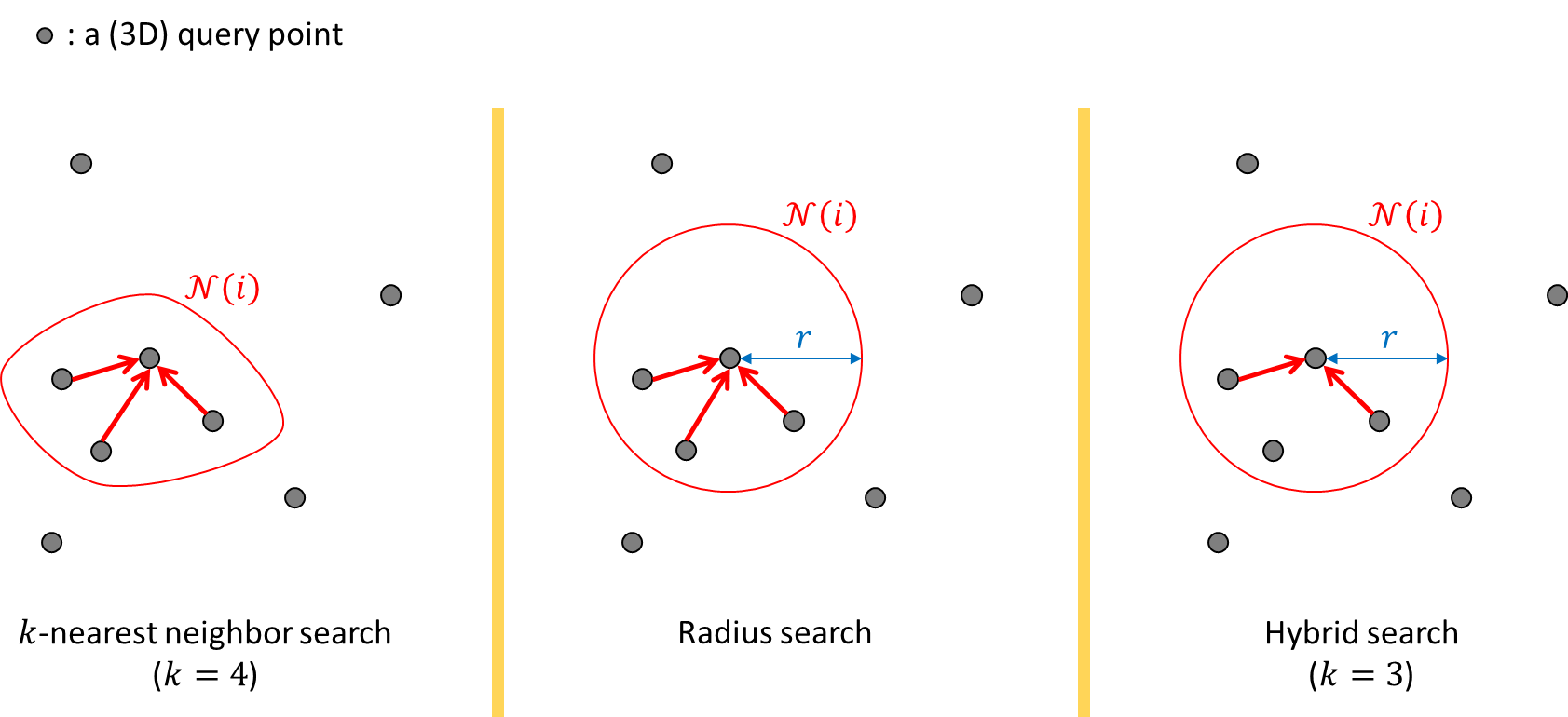
먼저 k-nearest neighbor search의 방법으로 가장 가까운 k개의 point를 설정하는 것이다. k개의 point를 찾기 위해서 거리를 계산하고 크기 순으로 정렬한 다음 k개를 뽑는 형태이다.
다음으로는 radius search로, 일정한 길이인 반지름을 설정한 다음, 설정한 반지름에 해당하는 원 안의 point를 정하는 방식이다. 이 방식은 모든 point 사이의 거리를 계산할 때 효율적으로 계산할 수 있다는 장점이 있다. r보다 큰 point는 계산할 필요가 없기 때문이다.
마지막으로 앞의 2가지 방식을 합친 것으로 hybrid search 방식이 있다. r(반지름) 안에 들어가는 point를 찾은 다음 정해진 k의 개수보다 많다면 더 가까이 있는 k개의 point를 설정하는 방식이다.

이러한 로컬리티를 이용해서 PointNet에 로컬리티 특성을 추가한 것이 아래 그림의 PointNet++이다.
N은 point clouds의 크기를, d는 point의 dimension으로 3D points를 사용하기에 d는 3을, PointNet++에서는 local neighbor를 정의할 때 hybrid search 방식을 선택하는데 여기에서 개수 k에서 개수를 K로, C는 각 feature map에서 channel dimension을 말한다.

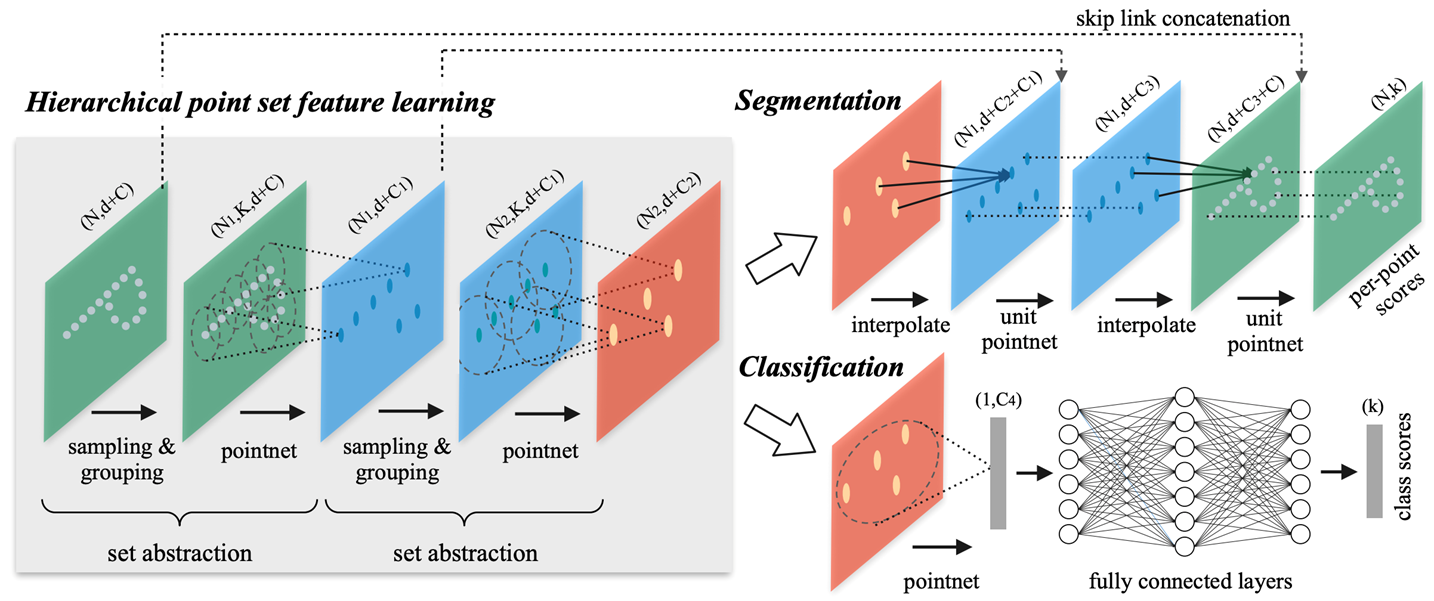
input cloud points가 들어오면, conv2d에서 feature map을 줄여나가듯이 3D에서도 포인트를 샘플링해서 feature map을 줄인다. 그렇게 레졸루션이 차이가 나기 때문에 hierarchical point set feature learning이 가능하게 된다. 그리고 2D의 U-Net에서 인코더-디코더처럼, PointNet++ 구조에서는 feature hierarchical가 존재하기에 segmentation 부분에서 디코더를 수행할 수 있게 된다.

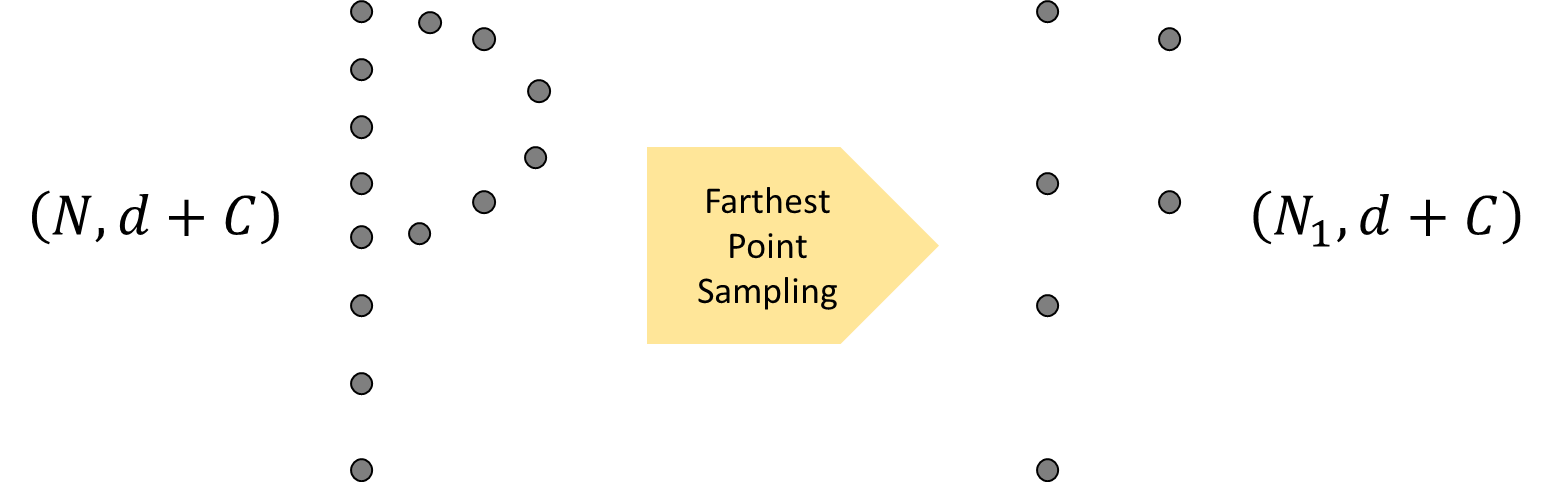
샘플링은, xyz 3차원 coordinates of input points에 해당하는 feature를 가지는 N크기의 'd' dimension이 Farthest Point Sampling을 통해서 N보다 작은 N1 크기의 point를 'sampling'한다.
그리고 샘플링 된 point를 Ball query(hybrid search)을 이용하여 'grouping'을 진행한다.
그러면 아래와 같이 3차원의 N, K, d+c shape의 3차원 array 형테로 neighbor features를 정의할 수 있게 된다.

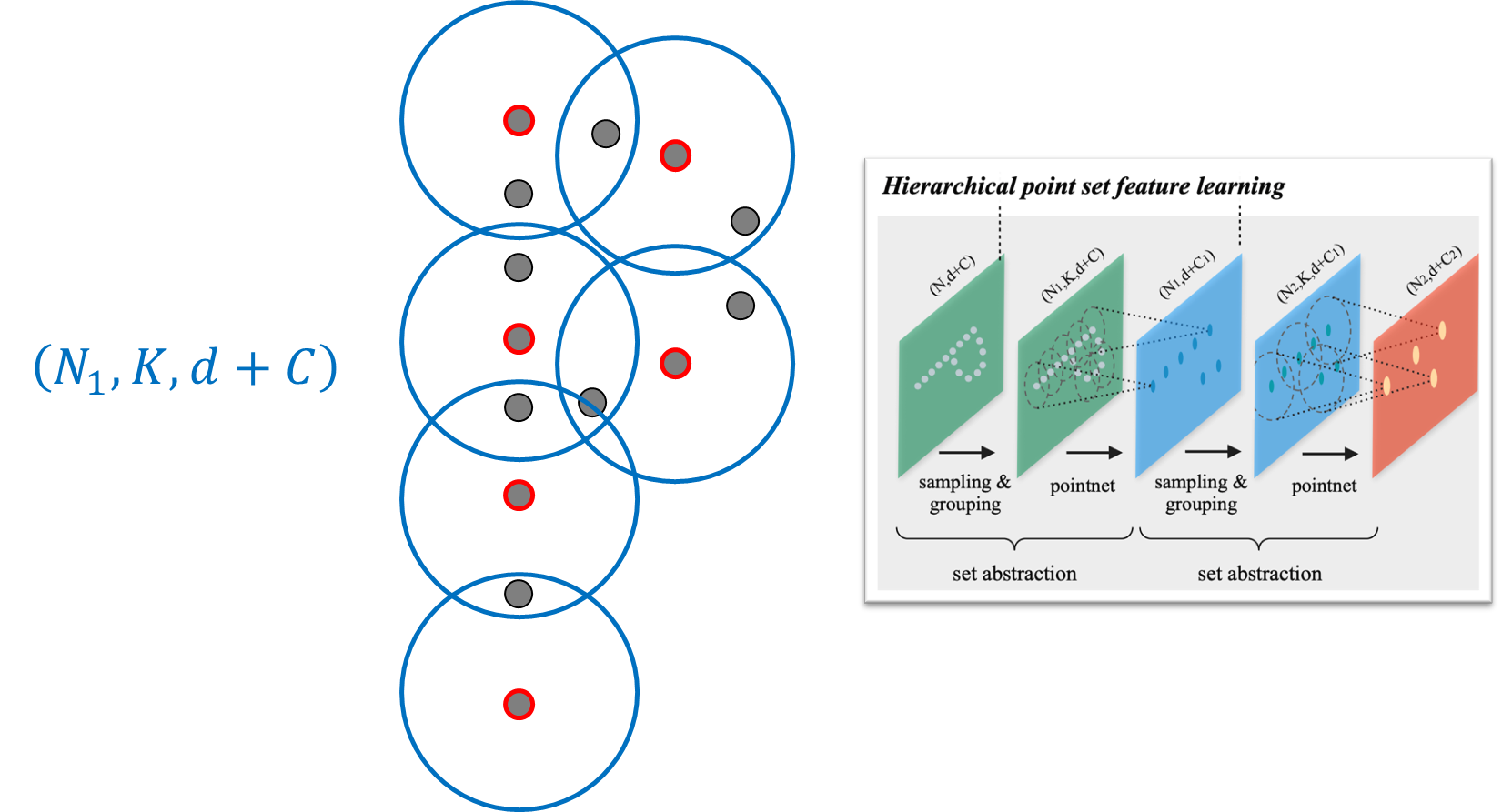
이 후에 PointNet을 적용시키게 되는데, PointNet 아키텍처 그림에서 n*3에서 n에 해당하는 point clouds가 neighbor features로 들어가게 된다.

이런 과정을 거쳐서 인코딩이 된 feature map을 다시 디코더 과정인 Upsampling을 거치게 된다.
인코더 단에서 중간 단계의 레졸루션 point clouds가 어떻게 생겼는지 알고 있기 때문에 해당 구조를 Upsampling 과정에 그대로 사용하게 된다. 그리고 U-Net과 같이 skip connector를 통해서 concatenate하게 되고, convolution을 수행하듯이 pointNet으로 feature를 섞어주는 과정이 추가로 들어간다.

Point Transformer

Point Transformer는 PointNet++과 유사하지만 k-nearest neighbor search를 이용하여 neighbor를 정의하게 된다. hybrid search에서 r이 limmit을 설정하기에 장점도 있지만, point가 매우 조밀하거나 반대의 경우 k개의 포인트만 찾게 되어 영역이 많이 달라질 수 있다. 반면 k-nearest neighbor search는 local neighborhood에서 transformer 구조를 수행하는 방식으로 k개의 가장 가까운 neighbor를 보장함으로써 self-attention을 안정적으로 학습하는 효과가 있다.
그리고 self-attention을 통해서 feature를 학습하고 summation을 수행해서 feature learning을 하는 것이 다른 점이다.

Point Transformer도 아래의 그림과 같이 다운 샘플링과 업 샘플링을 하는데 그 방식은 PointNet++ 방식과 비슷하다.

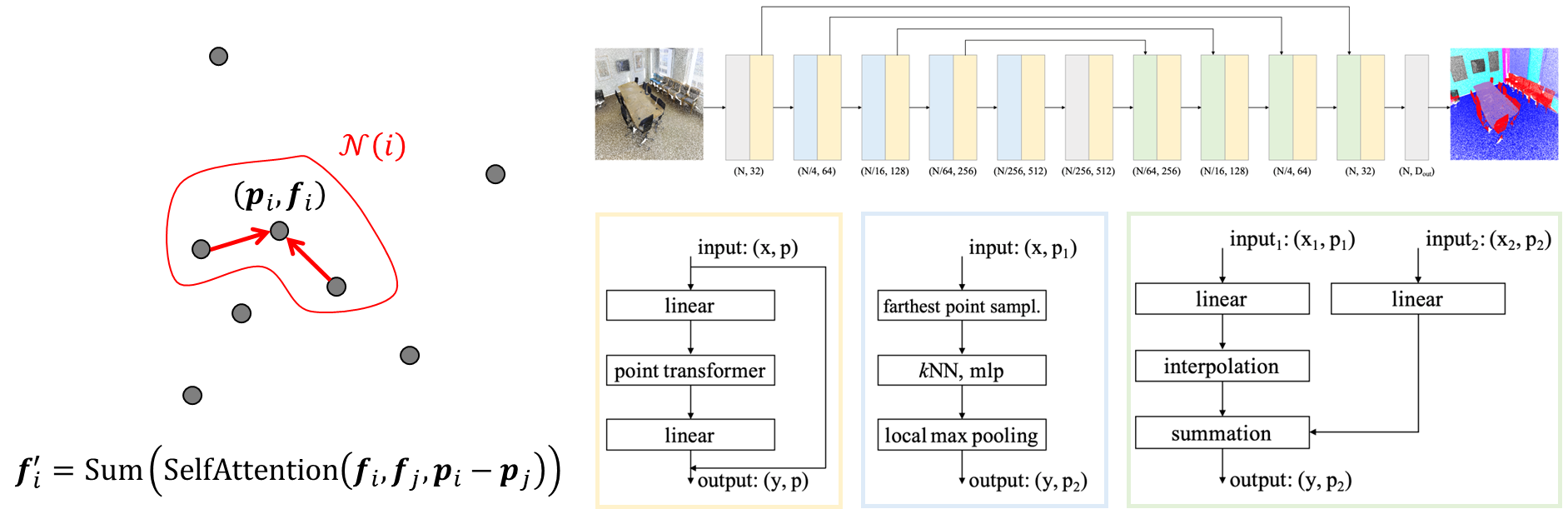
Local Self-Attention

Local Self-Attention은 중간의 feature에 따라서 conv kennel의 weight이 바뀌는 다이나믹 커널 웨이트를 가지고 있다.
아래의 그림에서 오른쪽처럼 일반적으로 kennel의 크기에 맞게 각 위치를 곱하고 더해서 output을 내뱉는 것과는 달리, 입력된 feature의 가운데 feature에서 query feature를 만들고 자기 자신을 포함한 neighborhood 안에 들어가는 features을 통해서 key를 만들고, query와 key의 similarities를 계산하여 합이 1이 되는 다이나믹한 kennel weight를 만든다. 그리고 local neighborhood를 value로 만들어 similarity weight랑 합쳐서 output을 내뱉게 된다.
일반적인 conv layer와 다른 점은 learned weights가 바뀌지 않는 것과 달리, Local Self-Attention은 local neighborhood에 존재하는 key들이 바뀌면 conv kennel과 similarity metrics가 바뀌어서 output도 바뀌게 된다.

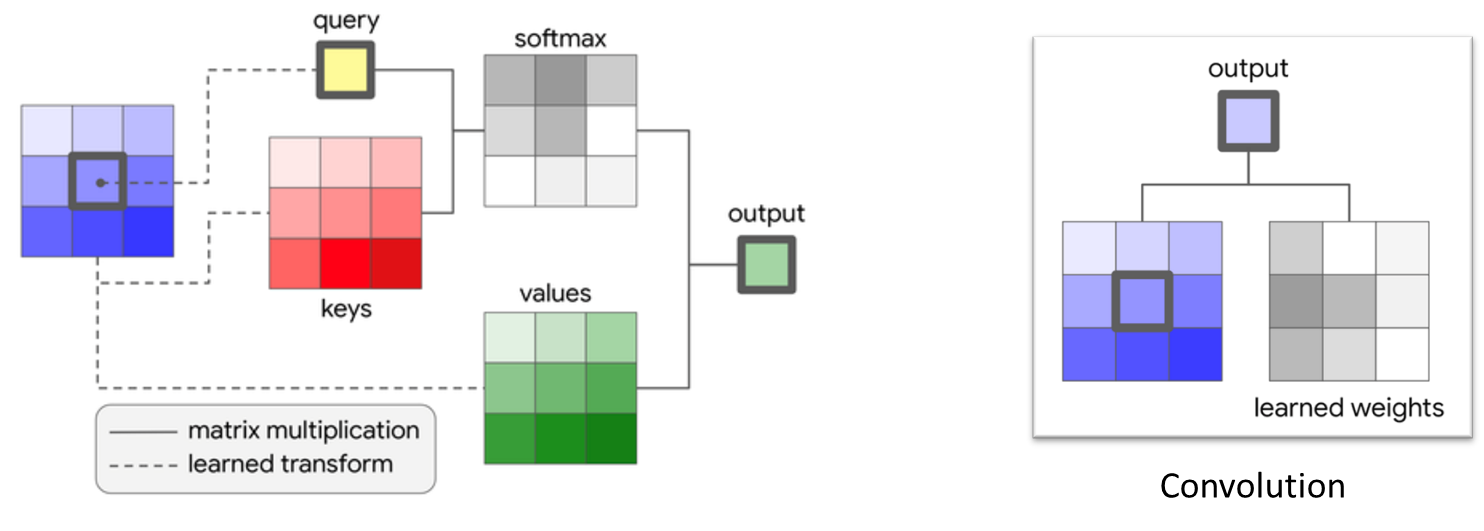
similarity는 먼저 query와 keys를 Dot-product를 하고 softmax와 같이 normalization을 진행하고, 다시 value와 Dot-product를 하여 정의하게 된다. query와 keys의 Dot-product한 것을 normalization function을 이용해서 summation을 하면 query와 keys의 similarity의 총합은 '1'이라는 제약 조건이 존재하게 된다. 그리고 values에 weighted sum을 진행하면 가장 similarity가 높은 key에 해당하는 value와 가장 유사하게 output이 출력된다.

이런 Local Self-Attention은 기본적으로 keys의 순서가 바뀌어도 output은 변하지 않는다는 특성이 있다. 그래서 문자나 이미지를 처리할 때는 local이 섞이는 것을 방지하기 위해 기존의 transformer과 같이 positional encoding을 더해주게 된다.

Point Transformer은 kNN search with local(vector) self-attention을 사용한다. 여기에서 델타가 positional encoding이다.

아래는 ate of the art performance** 결과이다.

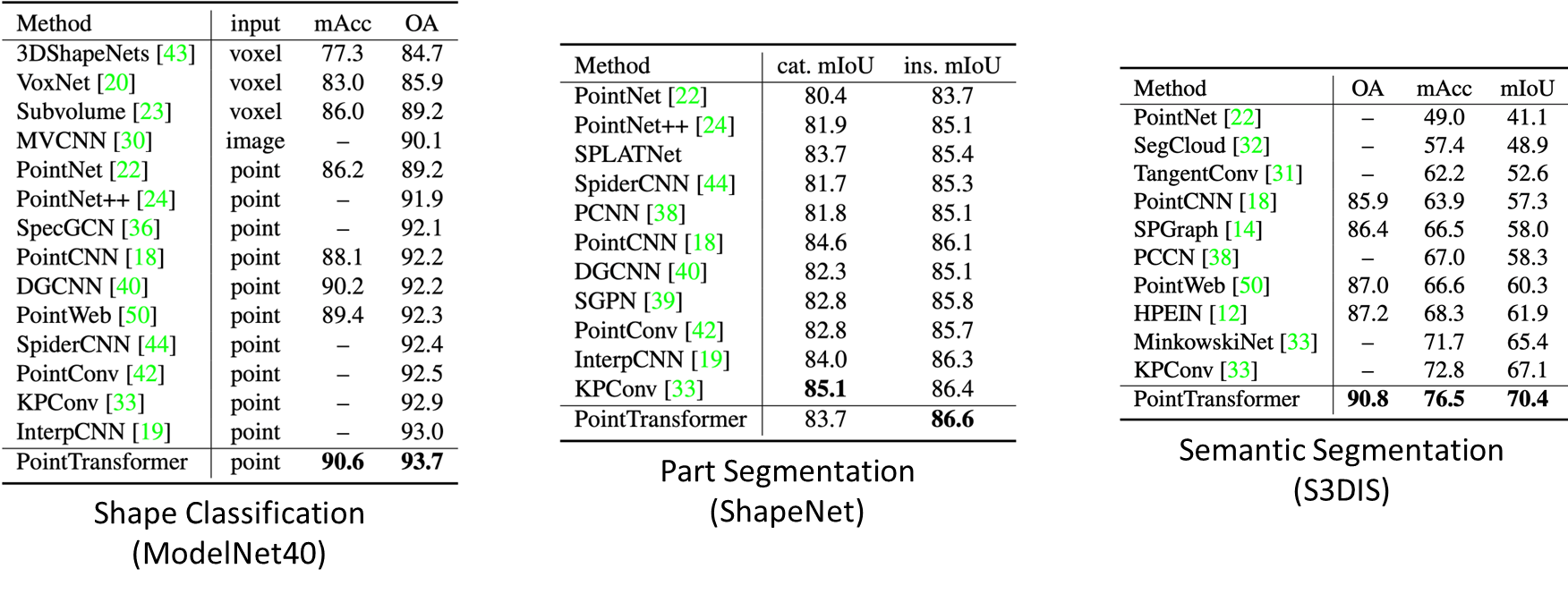
Point Transformer Network

k-Nearest Neighbor Search

data set points는 N개, query poins는 M개이고 M개의 query poins에 대해서 각각 k개의 가장 가까운 data set points를 찾는 kNN-search구현은 아래와 같다.

# 1 find_knn
def find_knn(point_cloud, k):
    N = len(point_cloud)

    delta = point_cloud.view(N, 1, 3) - point_cloud.view(1, N, 3)
    dist = torch.sum(delta ** 2, dim=-1)

    knn_dist, knn_indices = dist.topk(k=k, dim=-1, largest=False)

    return knn_dist, knn_indices
    
# 2 find_knn_general
def find_knn_general(query_points, dataset_points, k):
    M = len(query_points)
    N = len(dataset_points)
    
    # 1. Compute pairwise distance
    delta = query_points.view(M, 1, 3) - dataset_points.view(1, N, 3) # (M, N, 3)
    dist = torch.sum(delta ** 2, dim=-1) # (M, N)
    
    # 2. Find k-nearest neighbor indices and corresponding features
    knn_dist, knn_indices = dist.topk(k=k, dim=-1, largest=False) # (M, k) / # largest : False로 인자를 입력하면 가장 작은(<-> True : 기장 큰) top k개의 인덱스 반환
    
    return knn_dist, knn_indices

k-Nearest Neighbor Linear Interpolation

transition up 모듈 부분에서 linear 부분에 사용된다.

def interpolate_knn(query_points, dataset_points, dataset_features, k):
    M = len(query_points)
    N, C = dataset_features.shape
    
    # 1. Find k-nearest neighbor indices and corresponding features
    knn_dist, knn_indices = find_knn_general(query_points, dataset_points, k)
    knn_dataset_features = dataset_features[knn_indices.view(-1)].view(M, k, C)
    
    # 2. Calculate interpolation wegihts
    knn_dist_recip = 1. / (knn_dist + 1e-8) # (M, k)
    denom = knn_dist_recip.sum(dim=-1, keepdim=True) # (M, 1)
    weights = knn_dist_recip / denom # (M, k)
    
    # 3. Linear interpolation
    weighted_features = weights.view(M, k, 1) * knn_dataset_features # (M, k, 1) * (M, k, C) = (M, k, C)
    interpolated_features = weighted_features.sum(dim=1) # (M, C)
    
    return interpolated_features

Farthest Point Sampling

(N, 3)에서 M개로 Sampling하여 (M, 3)으로 바꿔주는 Farthest Point Sampling 부분이다. 샘플링을 할 때 각 샘플끼리 가장 멀리 떨어뜨려 샘플링 할 수 있게 만든다.

def farthest_point_sampling(points, num_samples):
    N = len(points)
    
    # 1. Initialization
    sampled_indices = torch.zeros(num_samples, dtype=torch.long)
    distance = torch.ones(N,) * 1e10
    farthest_idx = random.randint(0, N)
    
    # 2. Iteratively sample the farthest points
    for i in range(num_samples):
        # 2-1. Sample the farthest point
        sampled_indices[i] = farthest_idx
        
        # 2-2. Compute distances between the sampled point and other (remaining) points
        centroid = points[farthest_idx].view(1, 3)
        delta = points - centroid
        dist = torch.sum(delta ** 2, dim=-1) # (N,)
        mask = dist < distance
        distance[mask] = dist[mask]
        
        # 2-3. Sample the next farthest point
        farthest_idx = torch.max(distance, -1)[1]

    return sampled_indices

Point Transformer Layer

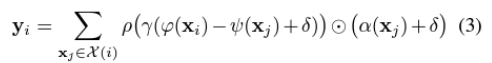
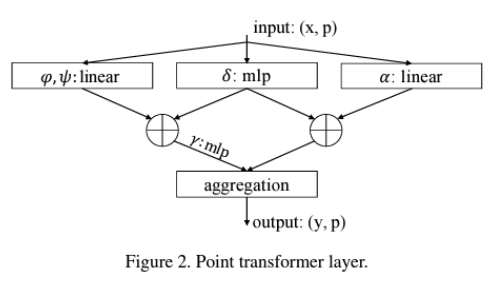
class PointTransformerLayer(nn.Module):
    
    def __init__(self, in_channels, out_channels, k):
        super(PointTransformerLayer, self).__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.k = k
        
        # Linear porjection : query, keys, values
        self.linear_q = nn.Linear(in_channels, out_channels, bias=False)
        self.linear_k = nn.Linear(in_channels, out_channels, bias=False)
        self.linear_v = nn.Linear(in_channels, out_channels, bias=False)
        
        # Linear porjection 이 후의 MLP Attention
        self.mlp_attn = nn.Sequential(
            nn.BatchNorm1d(out_channels),
            nn.ReLU(inplace=True),
            nn.Linear(out_channels, out_channels),
            nn.BatchNorm1d(out_channels),
            nn.ReLU(inplace=True),
            nn.Linear(out_channels, out_channels)
        )
        
        # Positional encoding
        self.mlp_pos = nn.Sequential(
            nn.Linear(3, 3), # input : 3차원 relative vector
            nn.BatchNorm1d(3),
            nn.ReLU(inplace=True),
            nn.Linear(3, out_channels)
        )
        
        # softmax normalization 
        self.softmax = nn.Softmax(dim=1)
        
    def forward(self, points, features):
        N = len(points)
        
        # 1. Query, key, and value projections
        f_q = self.linear_q(features) # (N, C_out)
        f_k = self.linear_k(features) # (N, C_out)
        f_v = self.linear_v(features) # (N, C_out)
        
        # 2. Find kNN for local self-attention
        knn_dist, knn_indices = find_knn(points, self.k) # (N, k)
        knn_points = points[knn_indices.view(-1)].view(N, self.k, 3)
        knn_k = f_k[knn_indices.view(-1)].view(N, self.k, self.out_channels)
        knn_v = f_v[knn_indices.view(-1)].view(N, self.k, self.out_channels)
        
        # 3. Calculate the relative positional encoding
        rel_pos = points.view(N, 1, 3) - knn_points # (N, k, 3)
        rel_pos_enc = self.mlp_pos(rel_pos.view(-1, 3)).view(N, self.k, -1) # (N, k, C_out)
        
        # 4. Vector similarity(query - keys + Rel_pos) and Normalization
        vec_sim = f_q.view(N, 1, self.out_channels) - knn_k + rel_pos_enc
        weights = self.mlp_attn(vec_sim.view(-1, self.out_channels)).view(N, self.k, self.out_channels)
        weights = self.softmax(weights) # (N, k, C_out)
        
        # 5. Weighted sum
        weighted_knn_v = weights * (knn_v + rel_pos_enc) # (N, k, C_out)
        out_features = weighted_knn_v.sum(dim=1) # (N, C_out)
        
        return out_features

Point Transformer block

class PointTransformerBlock(nn.Module):
    
    def __init__(self, channels, k):
        super(PointTransformerBlock, self).__init__()
        self.linear_in = nn.Linear(channels, channels)
        self.pt_layer = PointTransformerLayer(channels, channels, k)
        self.linear_out = nn.Linear(channels, channels)
        
    def forward(self, points, features):
        out_features = self.linear_in(features)
        out_features = self.pt_layer(points, out_features)
        out_features = self.linear_out(out_features)
        out_features += features # skip conn
        
        return out_features

transition down

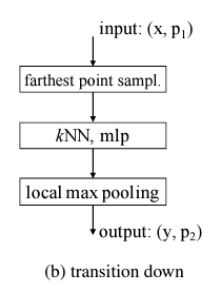
class TransitionDown(nn.Module):
    
    def __init__(self, channels, num_samples, k):
        super(TransitionDown, self).__init__()
        self.channels = channels
        self.num_samples = num_samples
        self.k = k
        
        self.mlp = nn.Sequential(
            nn.Linear(channels, channels, bias=False),
            nn.BatchNorm1d(channels),
            nn.ReLU(inplace=True),
            nn.Linear(channels, channels, bias=False),
            nn.BatchNorm1d(channels),
            nn.ReLU(inplace=True)
        )
        
    def forward(self, points, features):
        N = len(points)
        
        # 1. Farthest point sampling
        sampled_indices = farthest_point_sampling(points, self.num_samples)
        sampled_points = points[sampled_indices] # shape : (self.num_samples, 3)
        
        # 2. kNN search : q_point, d_point 가 다른 상황
        knn_dist, knn_indices = find_knn_general(sampled_points, points, self.k) # (M, K)
        
        # 3. MLP
        knn_features = features[knn_indices.view(-1)] # (M*K, C)
        out_knn_features = self.mlp(knn_features)
        out_knn_features = out_knn_features.view(self.num_samples, self.k, -1) # shape : (M, k, C)
        
        # 4. Local max pooling
        out_features = out_knn_features.max(dim=1)[0]
        
        return sampled_points, out_features

transition up

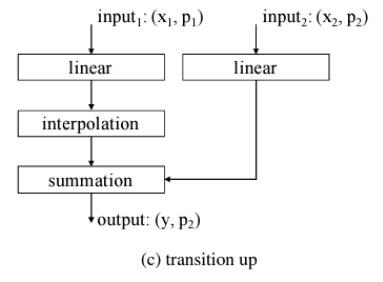
class TransitionUp(nn.Module):
    
    def __init__(self, up_channels, down_channels, out_channels):
        super(TransitionUp, self).__init__()
        self.linear_up = nn.Linear(up_channels, out_channels)
        self.linear_down = nn.Linear(down_channels, out_channels)
        
    def forward(self, up_points, up_features, down_points, down_features):
        # 1. Feed-forward with the down linear layer
        down_f = self.linear_down(down_features)
        
        # 2. Interpolation
        interp_f = interpolate_knn(up_points, down_points, down_f, 3) # (N, C_out)
        
        # 3. Skip-connection
        out_f = interp_f + self.linear_up(up_features)
        
        return out_f