강의 영상 주소 : https://www.youtube.com/watch?v=WUazOtlti0g&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=11

해당 슬라이드: https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture11.pdf

✍️ [~ p.33] 내용 요약정리

< Intro >

---

• 지난 시간에는 train하기 전에 처리하고 설정해야할 Activation functions, data preprocessing, weight initalization, regularization에 대해 알아보았음

• 이번 Training Neural Networks(part2)에서는 training하면서 고려해야할 것들에대해 알아볼 것임

---

Learning Rate Schedules

이전에 배웠던 SGD, SGD+Momentum 등과 같은 optimization기법들은 다 learning rate를 하이퍼파라미터로 가지고 있었다.

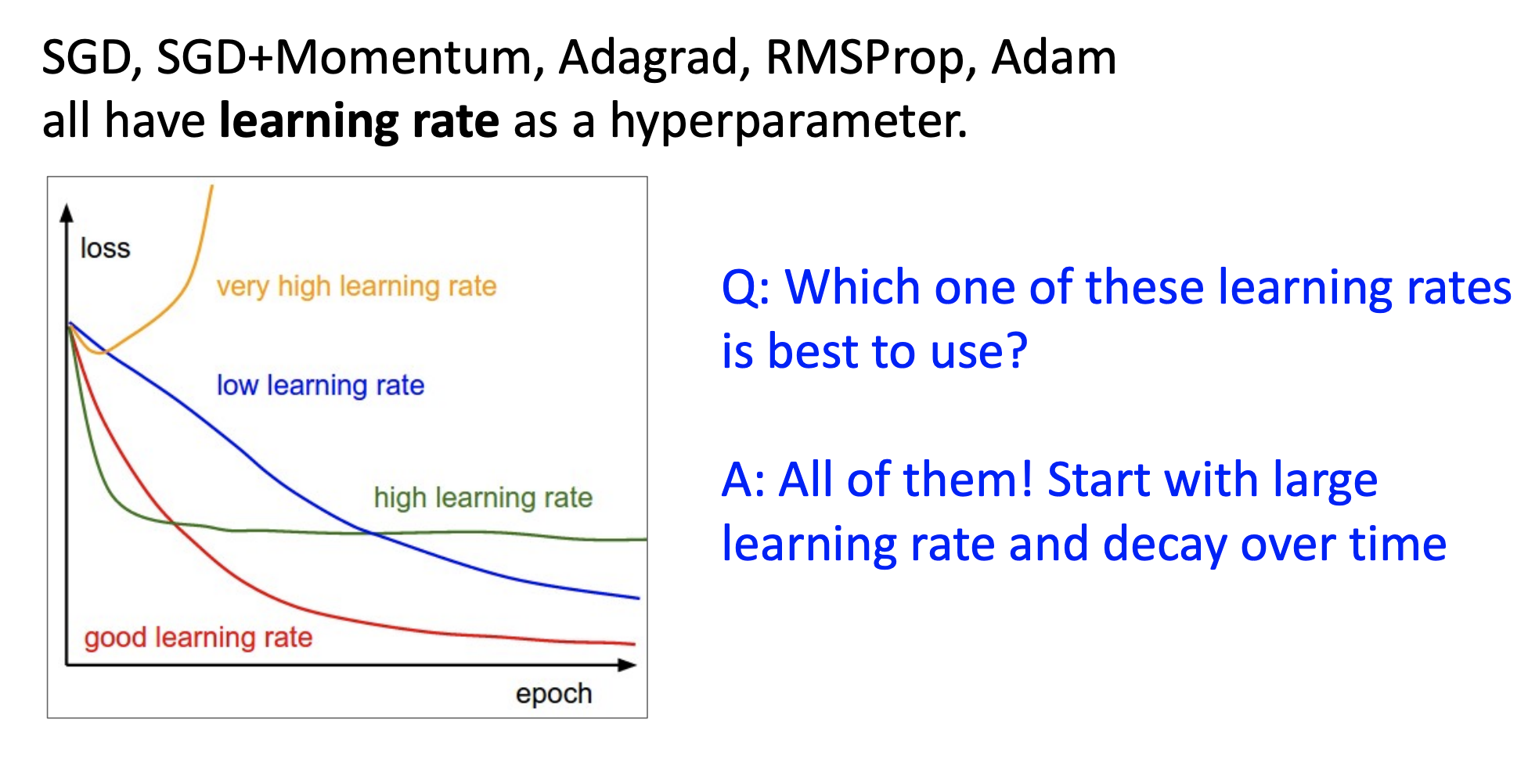
아래 그래프는 임의의 learning rate를 다 집어 넣어봤을 때 보통 우리가 볼 수 있는 loss 곡선들임

• 첫번 째로 노란색 그래프를 보면 learning rate를 매우 높게 설정한 경우인데 처음에는 loss가 떨어지는 것 같더니 그래프가 바깥으로 나가져 버릴 정도로 오히려 loss가 높아지는 것을 볼 수 있음

• 두번 째로 파란색 그래프는 learning rate를 낮게 설정한 경우이다. 노란색 그래프와 다르게 loss가 점점 내려가긴 하지만 매우 느리게 내려가기 때문에 epoch를 더 많이 돌려봐야할 수 있음

• 세번 째로 녹색 그래프는 엄청 높지도 낮지도 않고 살짝 높게 설정한 learning rate인데 맨 처음에는 loss가 빠르게 내려가는 것 같지만 이런 경우에는 더 낮아질 수도 있지만 더 낮아지지 않고 flat하게 유지되는 상황이 될 수 있음

• 결론적으로 우리가 추구하는건 빨간색 그래프 경우인데 어떻게 최적의 learning rate를 찾을 수 있을까?

• 명확한 답은 없지만 높은 learning rate에서 시작을 하고 epoch가 늘어날수록 learning rate를 낮추는 방법이 이상적인 방법이지 않을까하고 생각을 해볼 수 있다.

Learning Rate Schedule

training동안 시간이 지남에 따라 learning rate를 변경시키는것을 learning rate schedule이라고 함

1) Step schedule

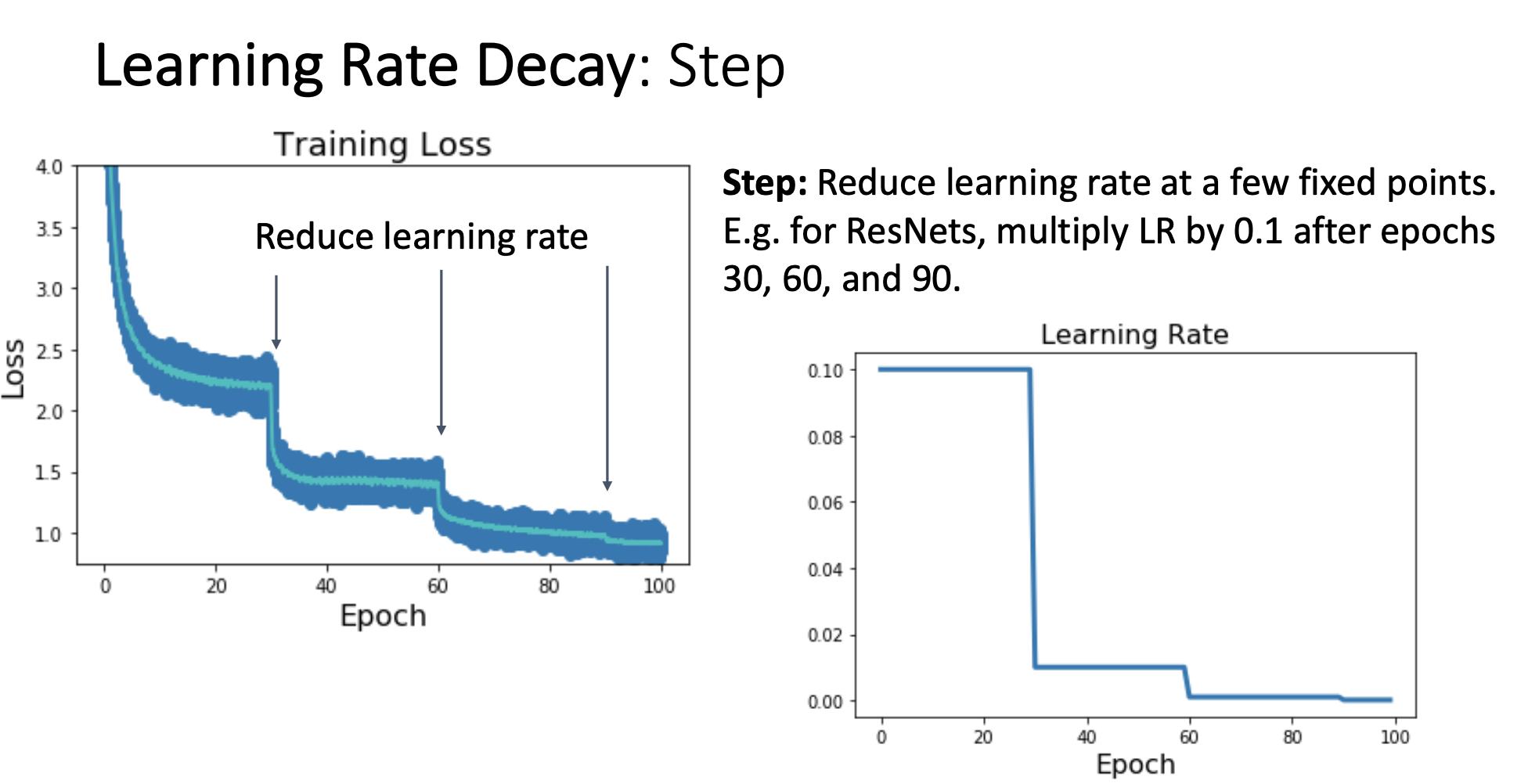
어떤 고정된 지점들에서 learning rate를 낮추는 것

• 오른쪽 그래프는 epoch 30이후에 처음에 설정했던 learning rate에 0.1을 곱해줘서 learning rate가 1/10로 떨어지게 하고 epoch 60이후에 또 0.1을 곱해줘서 learning rate를 떨어지게 하는 내용을 표현한 그래프이다.

• 왼쪽 그래프는 오른쪽 그래프처럼 learning rate를 함에 따라 loss곡선이 어떻게 되는지 보여주는 그래프이다.

• 여기서 점 하나하나는 iteration 한 번해서 파라미터 업데이트한 이후의 loss값이다.

• 파란색 점들 중간에 있는 민트색 곡선은 moving average인데
  이 moving average는 최근 100번의 iteration 동안에 loss값의 average를 취한 것이다.

• 이러한 step learning rate schedule은 step마다 learning rate를 고정시킬 epoch의 범위, step마다 learning rate 를 감쇠시킬 decay rate가 새로운 hyperparameter로 추가되는 문제가 있다.

2) Cosine schedule

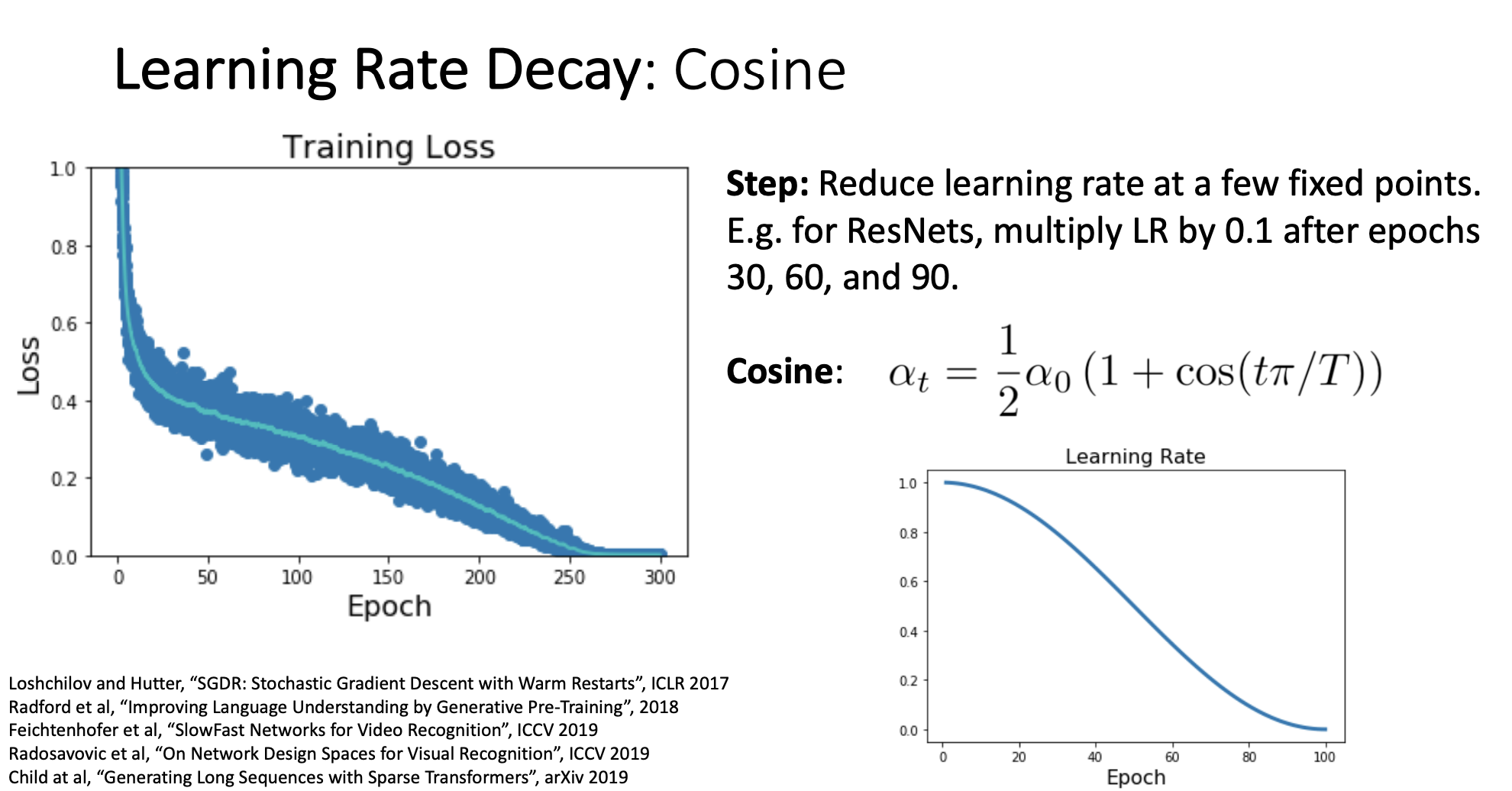
• 위에 보았던 Step learning rate schedule과는 달리 decay rate나 epoch의 범위를 설정해 줄 필요 없이 위 그림의 공식을 따라 매 epoch마다 learning rate을 decay시키게 된다.

• 위에 공식을 사용하면 오른쪽 그림과 같이 초반에는 high learning rate를 사용해서 학습이 빠르게 진행되고 학습의 끝에서는 learning rate가 0에 가까워지게 감쇠됨

• cosine learning rate decay schedule은 설정해줄 hyperparameter가 $\alpha_0$(initial learning rate)와 T(train 시킬 전체 epoch 수)밖에 없어서 hyperparameter choice가 줄어든다는 장점이 있어 최근에 많이 사용됨

3) Linear schedule

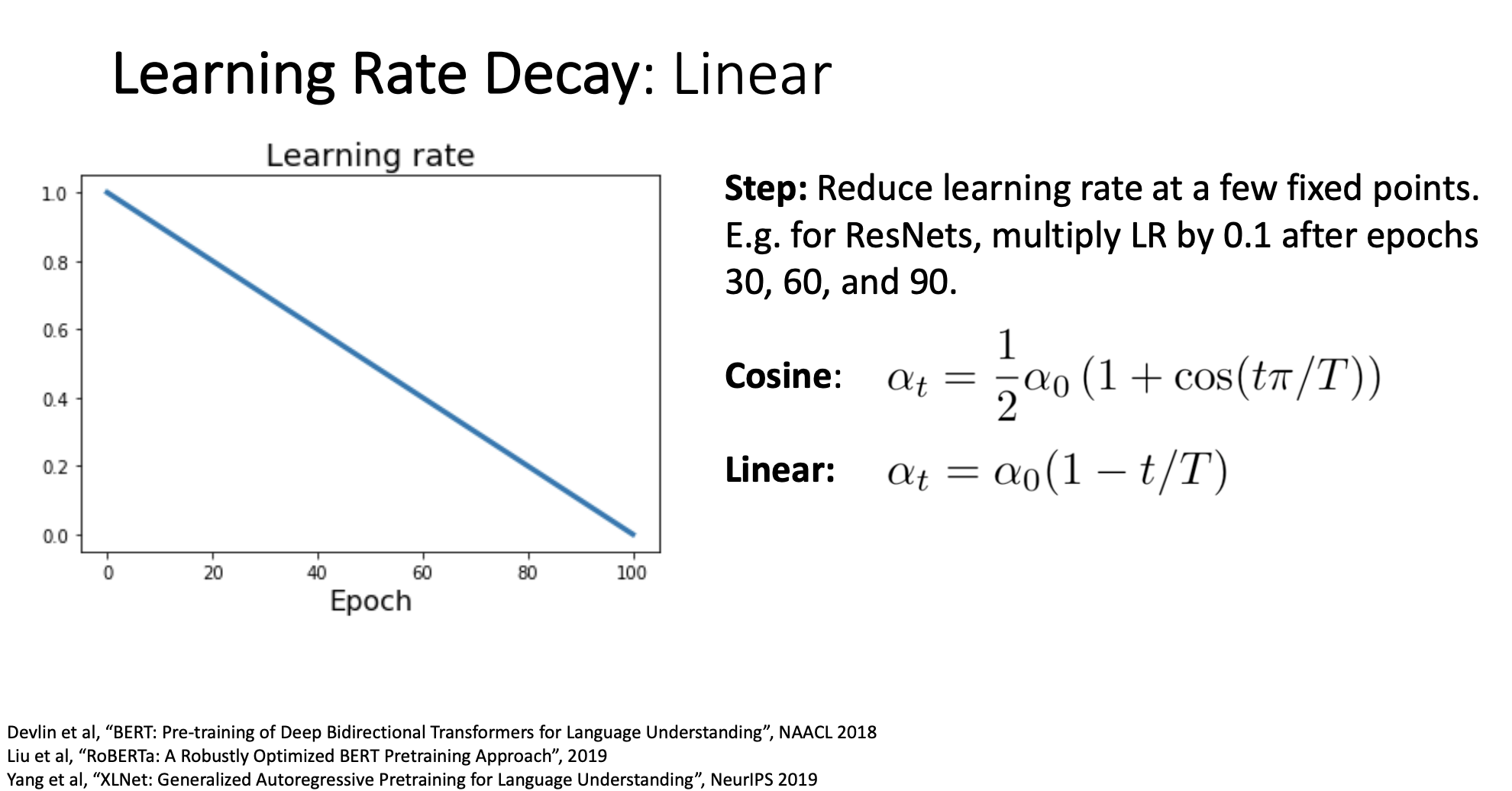
• 위에 그래프와 수식에서처럼 linear learning rate schedule은 간단하지만 자주 사용된다.

• 강의에서 justin johnson교수님이 말하길, 각 model마다, 각 problem마다 사람들이 사용하는 learning rate schedule은 다르며 이런 learning rate schedule들은 어느게 좋은지 비교할 수는 없다고 함.

• CV분야에서는 Cosine learning rate schedule을 많이 사용하고, large scale NLP에서는 linear learning rate schedule을 많이 사용한다고함

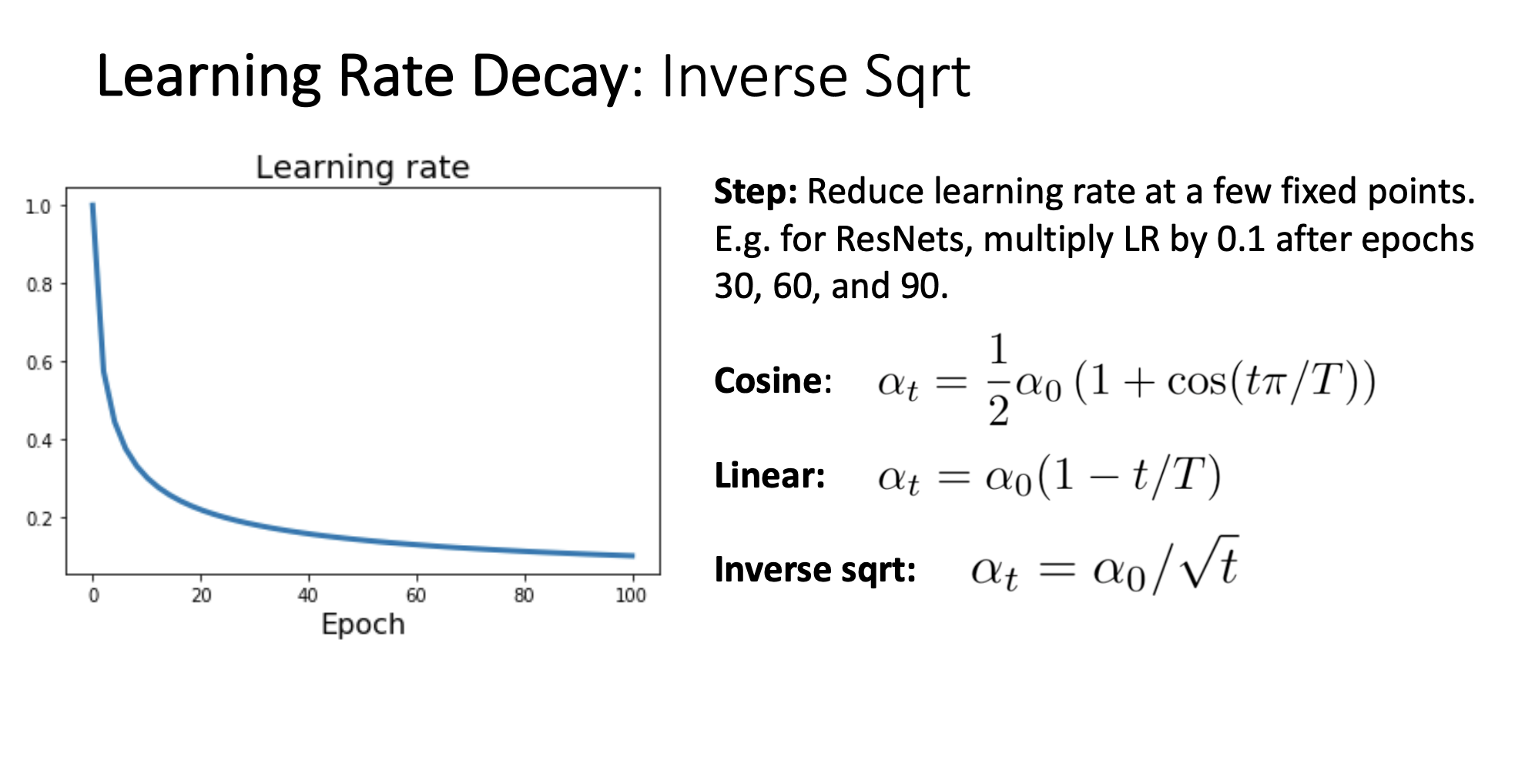
4) Inverse Sqrt schedule

• Inverse square root learning rate schedule은 Cosine, Linear와 다르게 거의 사용하지 않음

• Cosine schedule과 비슷한 Learning rate 그래프를 나타내지만, Inverse Sqrt의 경우 더 빠르게 감소 되는것을 알 수 있습니다.

• 근데 Cosine과 비교했을 때, Cosine 그래프를 보면 Cosine곡선의 특성상 초반에 learning rate가 되게 느리게 감소하는데

• 위의 이유로 Learning Rate Decay를 고려할 때 Inverse Sqrt보다 Cosine이 parameter space를 더 넓게 탐색한다고 생각을하고 Cosine decay를 더 많이 사용

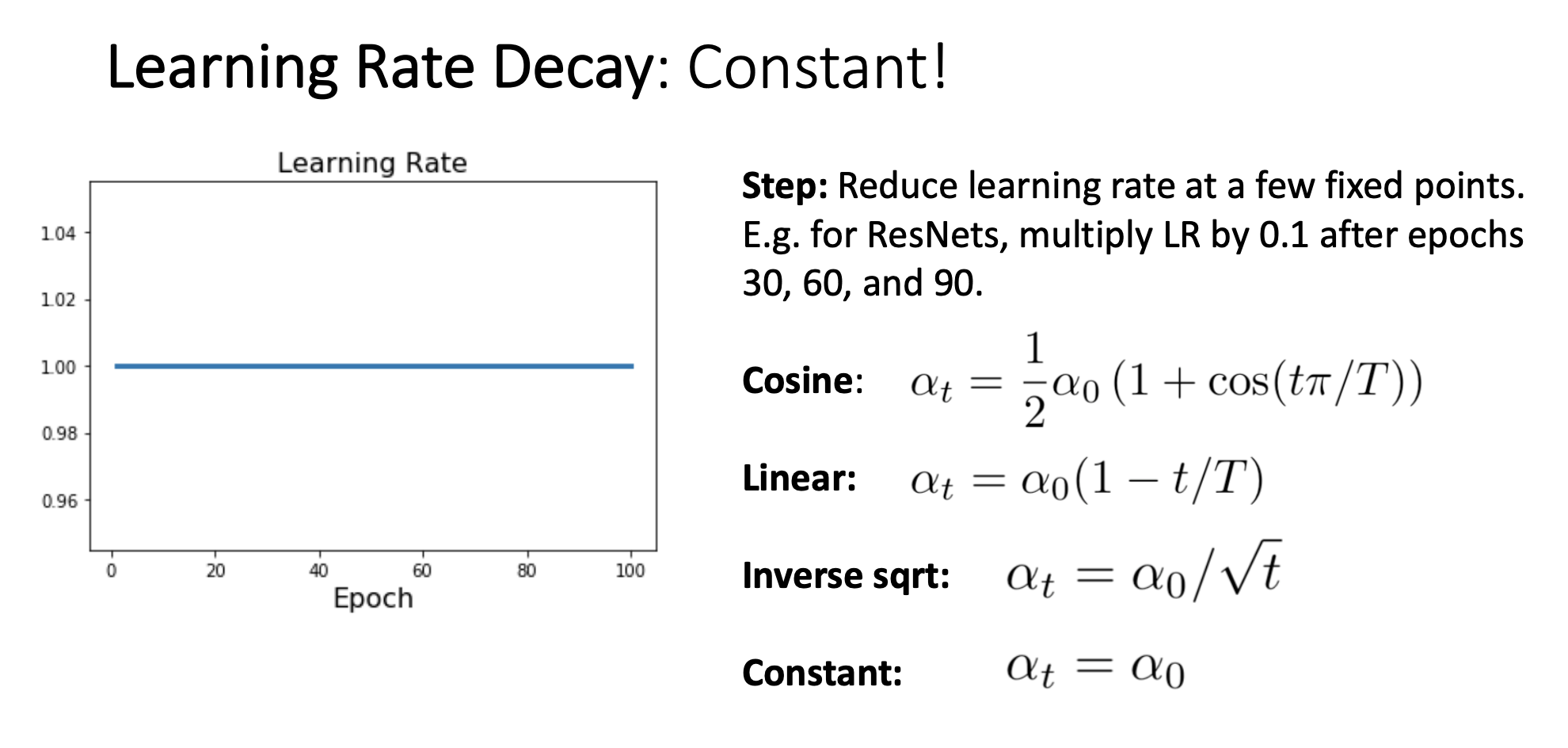
5) Constant schedule

• 우리가 가장 흔하게 볼 수 있는 learning rate schedule

• 이 Constant schedule은 다른 복잡한 laerning rate schedule과 비교해 model, problem에 따라 성능이 좋아질 수도 나빠질 수도 있으며, 가능한 빠르게 model을 만들어야 할때는 좋은 선택이 될 것이다.

• 또한 momentum같은 optimizer를 사용할때는 복잡한 learning rate decay schedule을 사용하는것이 좋지만 Adam or RmsProp를 사용할때는 (Bias correction이 붙었으므로) learning rate decay가 중요하지 않기에 그냥 Constant learning rate를 사용하는것이 좋다고 함

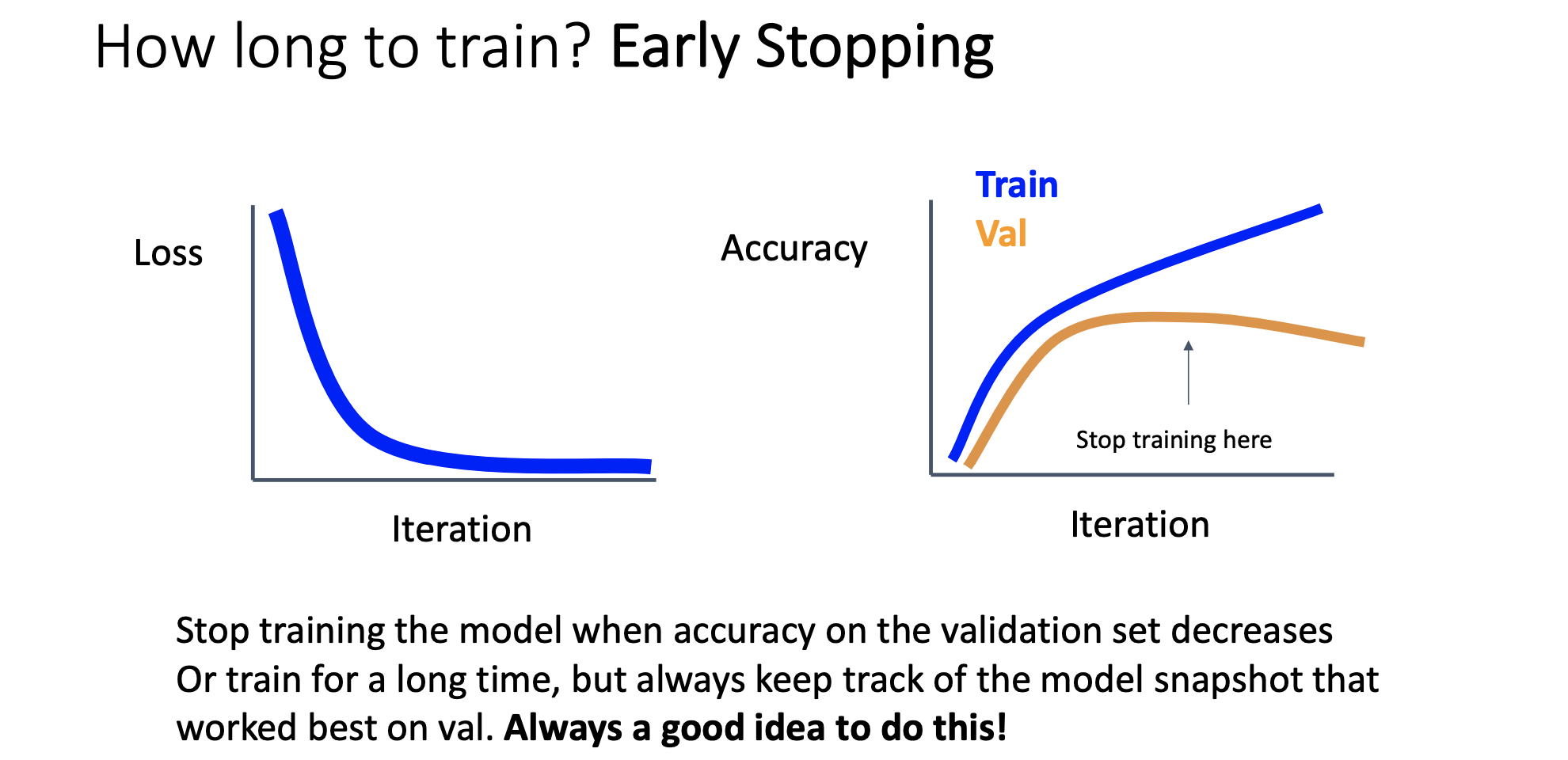
Early Stopping

• 우리가 얼만큼의 epoch or iteration으로 model을 훈련시켜야 할 지 모르겠을때 사용할 수 있는 좋은 mechanism이다.

• 오른쪽 그래프처럼 Accuracy는 train set에서는 맞게 점점 올라가는데 validation accuracy는 점점 감소하게 되면 둘의 차이가 벌어지는데 차이가 벌어진다는건 train set에 오버피팅이 되려고 한다는 것이기 때문에 그 전에 멈춰야함

• 둘의 차이가 벌어지기 전 iteration의 최적점을 찾아 training을 중지시키는 것이 Early Stopping이다.

• 강의에서는 Early Stopping을 사용하길 권장함

Choosing Hyperparameters

---

1) Grid Search

• 각 파라미터에 몇 가지 값을 설정해두고(로그함수에 선형적으로 설정), 모든 경우의 수를 학습하는 방식이다.

• GPU자원 소모가 굉장히 크다. (모든 경우 계산)

• 보통 많이 신경쓸 hyperparameter가 2개인데, 바로 Weight decay(L2 regularization의 strength)랑 learning rate이다.

• weight decay나 learning rate 모두 log-linear(같은 수씩 곱하는것(등비수열로))하게 고려함

• 이 경우의 수는 16(4x4)개의 hyperparameter choice를 비교해볼 수 있음

2) Random Search

• grid search말고 사람들이 고려하는게 random search이다.

• 각 파라미터의 범위를 선택하고 범위(로그함수에 선형적으로 설정)안에서 랜덤하게 선택하여 학습하는 방식이다.

• 아까는 예에서 $10^-4$, $10^-3$, $10^-2$, $10^-1$을 고려했는데 그렇게 하지말고
  여기서는 random variable을 -4 ~ -1사이에서 uniform하게 하나 뽑고 $10^U$을 취함(변수를 U라고 했을 때)

• 이렇게 하면 log scale의 space에서 uniform하게 $10^-4$과 $10^-1$ 사이에서 난수를 뽑을 수 있음

• learning rate도 마찬가지로 해볼 수 있음

• 이렇게 grid search, random search 이 두가지 방법으로 hyperparameter를 search할 수 있음

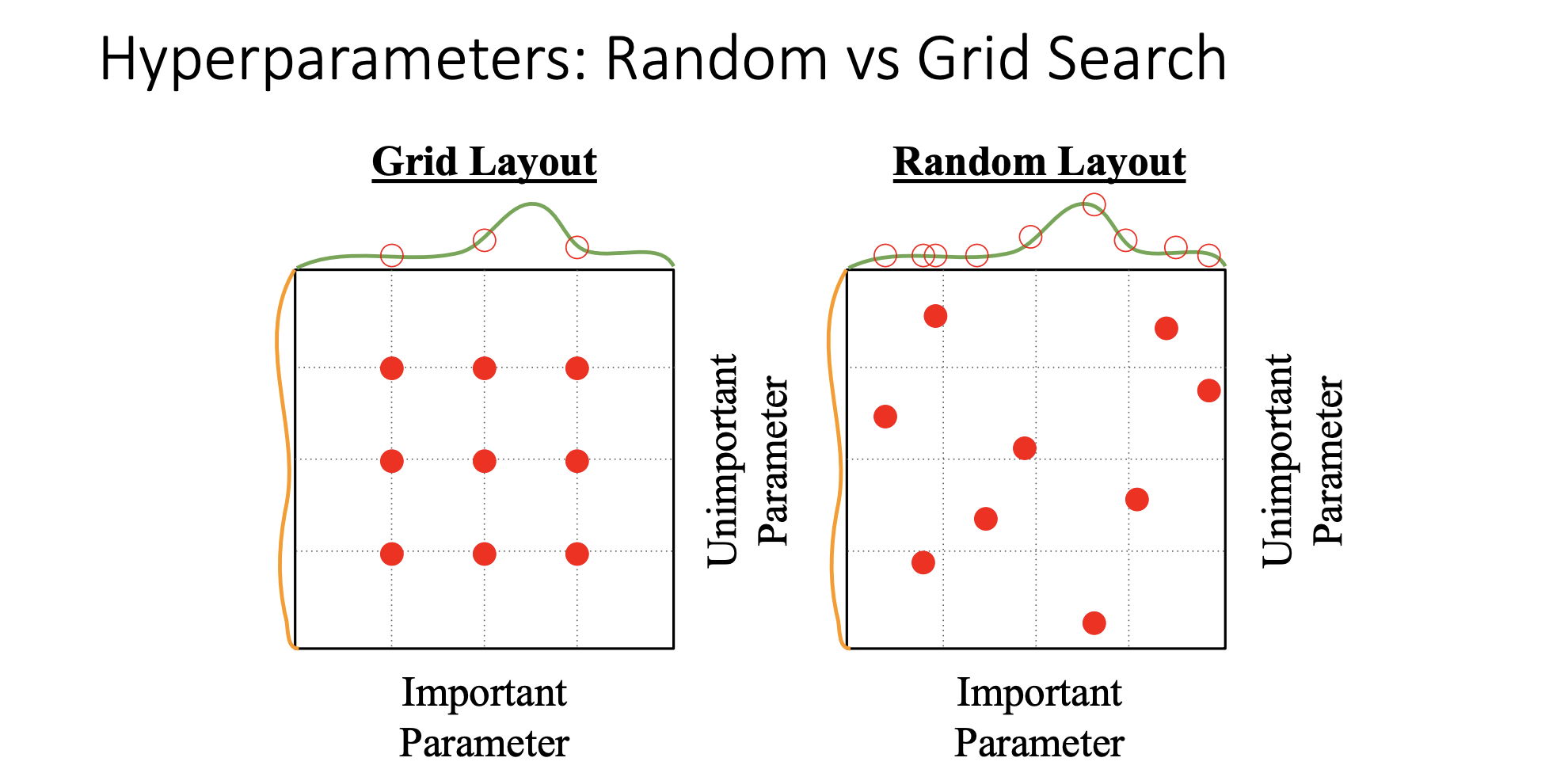
• 많은 사람들이 random search를 추천함 직관적으로는 위에 그림과 같음

• 데이터 셋과 모델에 따라 어떤 하이퍼 파라미터가 성능향상에 중요한지는 알 수 없음

• 모델 성능에 important parameter(녹색)와 그렇지 않은 파라미터(주황)가 존재하는데 grid search 방식은 좋은 성능을 갖는 파라미터가 무엇인지 판단에 어려움이 있다(녹색 그래프의 빨간색점이 균등하게 분포).

• 결과가 제공하는 정보가 제한적일 수 밖에 없다. 서로 같은 9번의 실험을 했지만 녹색 그래프의 파라미터에 대하여 grid search 방식은 3번 밖에 체크하지 못 했지만, random search방식은 9번이나 확인 할 수 있다.

• random search를 하면 우리도 모르는 important parameter에 대해서 다양한 choice를 고려할 수 있고 그만큼 녹색 곡선에서 좋은성능을 주는 choice를 찾아낼 가능성이 높아지게됨

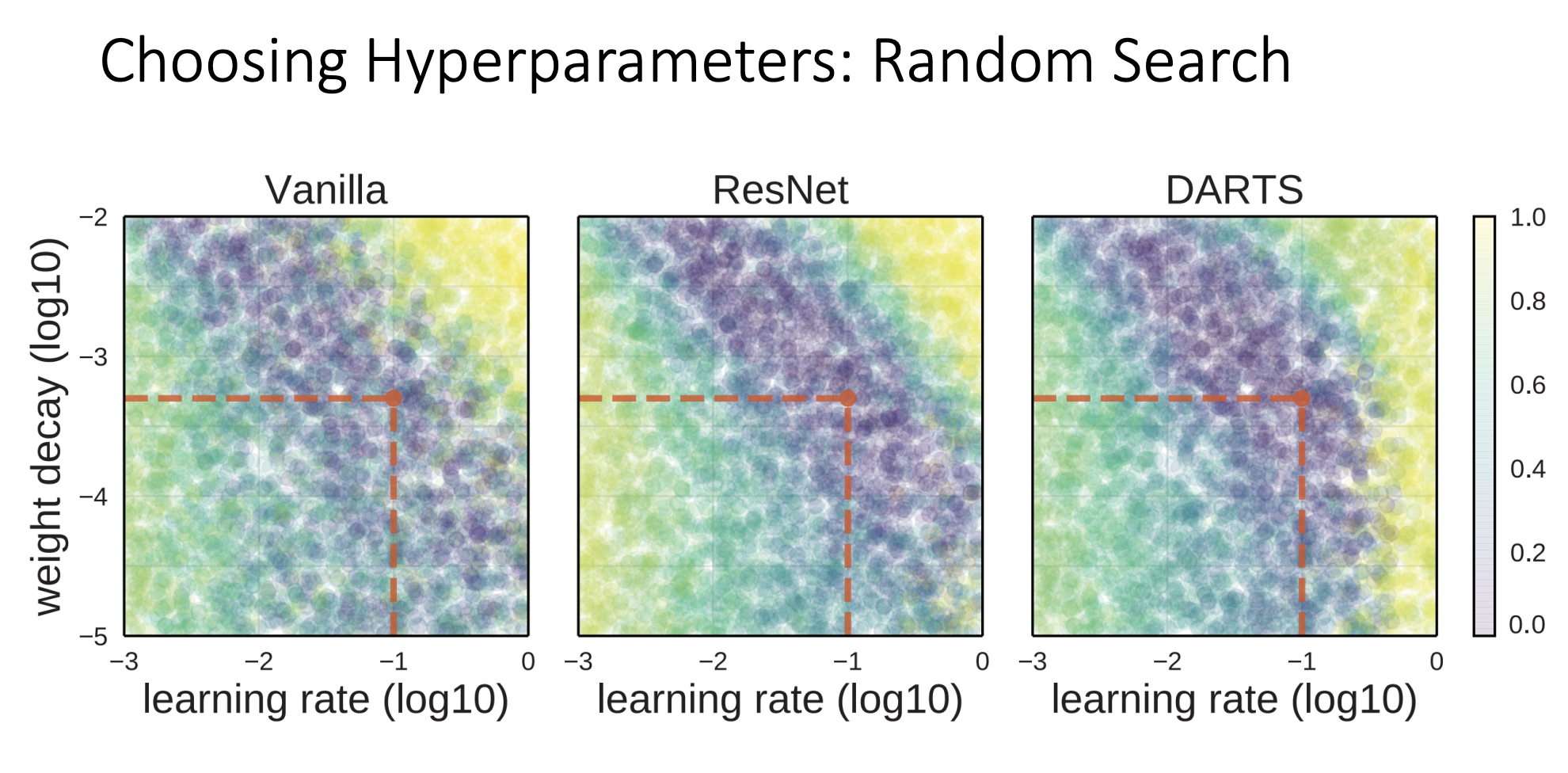
• 위 그림은 여러곳에서의 실험 결과를 나타냄

• random search를 통해서 많은 hyperparameter 중에 최적의 값을 찾는 일은 많은 GPU resources가 필요하기 때문에 일반적으로 사용하지 못함

• 그렇기때문에 hyperparameter를 어떻게 설정할지 많은 부분에 있어서 경험적인 부분을 적용하게 되는데, 한정된 GPU resources로 좀 더 체계적인 방식을 통해서 최적의 hyperparameter를 찾아야함

• 그래서 다음은 많은 GPU없이도 충분히 준수한 성능을 얻을 수 있는 가이드 같은 내용이 나옴

Choosing Hyperparameters

(without tons of GPUs)

Step 1 : check initial loss

• 첫 번째 단계는 먼저 코드를 작성한 후 weight decay를 사용하지 않고 sanity check를 통해서 random initialization후 첫 iteration에서 계산된 loss와 이론적인 loss의 기대값을 비교한다.

• 다시말해서 loss함수의 구조를 파악하고 weight decay를 적용하지 않은 상태에서 loss값이 무엇인지 확인한다.
  (예: C개의 클래스인 softmax일 때 log(C))

Step 2 : Overfit a small sample

• 매우 작은 5~10의 미니배치를 구성하여 학습정확도가 100%가 되는지 체크해 본다.

• 이때 regularization을 적용하지 않고 architecture(num of layer, size of each layer...), learning rate, weight initialization를 매우 작은 set에서 빠르게 조정하여 해당 architecture의 optimization이 올바르게 작동하는지 살펴보는 것이 목적임

• 작은 set에서 조정하는 이유는 이때 overfit되지 않는다면 실제 training set에서 fitting되지 않을 것이라는게 포인트이며 overfit되지 않는다면 optimization process에서 문제가 있다는 것을 뜻함

Step 3 : Find LR that makes loss go down

• Step3에선 이전 스텝에서 찾은 architecture에 작은 weight decay를 사용해 모든 training data 에 대해 training 시켜 100정도의 iteration안에 loss가 유의미하게 감소하는지 살펴보며 적절한 learning rate를 찾는다.

• 시도하기에 좋은 learning rate는 1e-1, 1e-2, 1e-3, 1e-4 라고 함

Step 4 : Coarse grid, train for ~1-5 epochs

• 이전 스텝에서 찾은 learning rate 와 weight decay 를 적용하여 몇개의 모델에 대해 1~5의 epoch 정도를 학습시킨다.

• 이는 training set을 넘어 valid set을 통해 모델의 일반화된 성능을 어느정도 파악할 수 있게 만들어 준다.

• 시도하기에 좋은 weight decay는 1e-4, 1e-5, 0 라고 한다.

Step 5 : Refine grid, train loger

• 이전 스텝에서 가장 괜찮은 모델에 대해 조금 더 길게(10~20 epoch)학습을 시켜본다. 이 때 learning rate decay 는 사용하지 않는다.

Step 6 : Look at learning curves

• 이전 스텝에서 학습한 model의 learning curves를 살펴본다.