Artificial Intelligence #06 Search2 Minimax algorithm

김서영·2024년 10월 17일

Artificial Intelligence 인공지능 2판

인공지능

목록 보기

5/13

1. 게임 프로그램

게임에서 최선의 수를 찾는 알고리즘을 학습하기 위하여, 불필요한 탐색을 막는 방법을 알아내야 한다.
이때 다음과 같은 속성을 가진 게임만을 고려한다.

두 명의 경기자 : 경기자들이 연합하는 경우는 다루지 않는다.
제로썸 게임 : 한 경기자의 승리는 다른 경기자의 패배이다. (협동적인 승리X)
순차적인 게임 : 차례대로 수를 두는 게임만을 대상

두 경기자를 MAX, MIN 라고 설정하고, 항상 MAX가 먼저 수를 둔다고 가정한다.

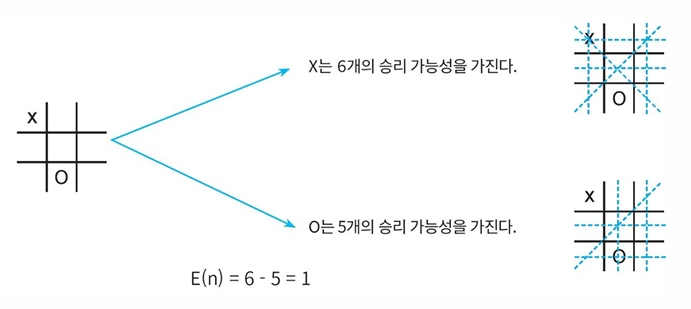
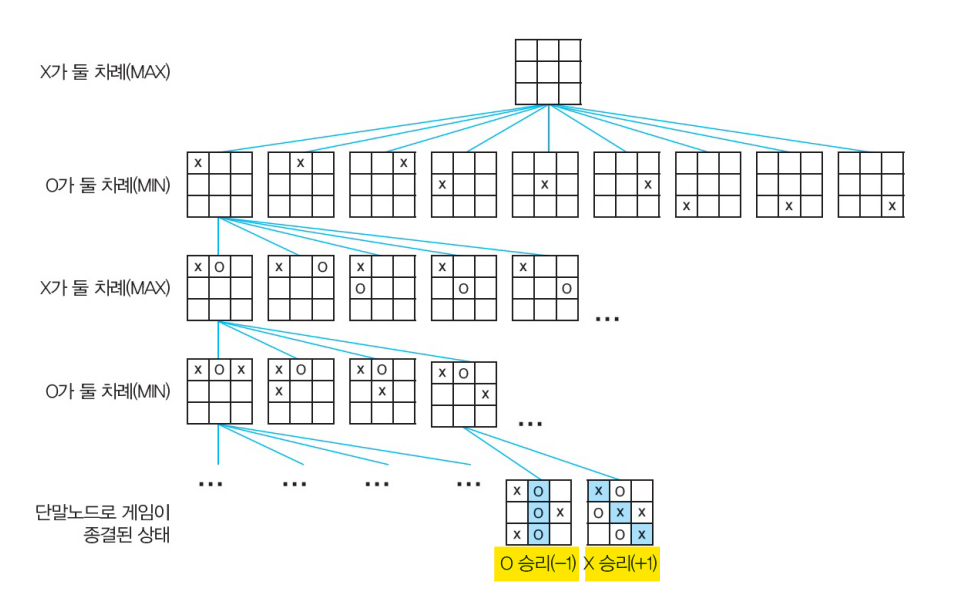
Tic-Tac-Toe에 대한 게임 트리

Tic-Tac-Toe : 오목과 유사한 외국의 게임으로 3X3 게임판에서 가로, 세로, 대각선으로 동일한 심볼을 먼저 만들면 승리

MAX(X) 플레이어가 이기면 +1점, X플레이어에 대해서는 최대값으로 가게끔 학습한다.
MIN(O) 플레이어가 이기면 -1점, O플레이어에 대해서는 최소값으로 가게끔 학습한다.
(비기면 평가값은 0점)

2. 미니맥스 알고리즘 (Minimax algorithm)

게임트리의 목표 상태는 승리에 해당되는 단말 상태이지만, 게임에서는 상대방이 탐색에 영향을 끼친다.
그렇기에 알고리즘을 만들기 위해서, 상대방(MIN)의 수를 예측할 수 없으니 항상 '최선의 수'를 둔다고 가정한다.
MAX는 항상 최선의 수를 두는 상대방(MIN)을 이기기 위한 알고리즘을 만들면 어떤 경우에서라도 이길 수 있다.

모든 함수의 값은 MAX 입장에서 만들어지기에, MIN 입장에서는 평가함수값이 낮은 것이 '최선의 수'이다

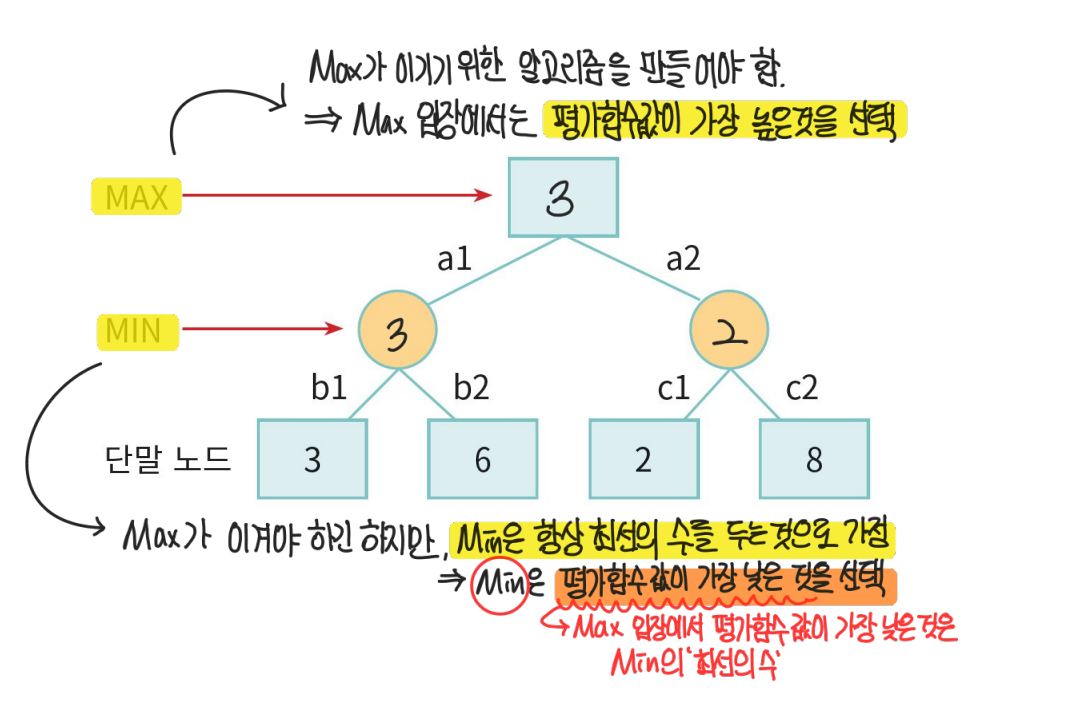
Minimax algorithm Example

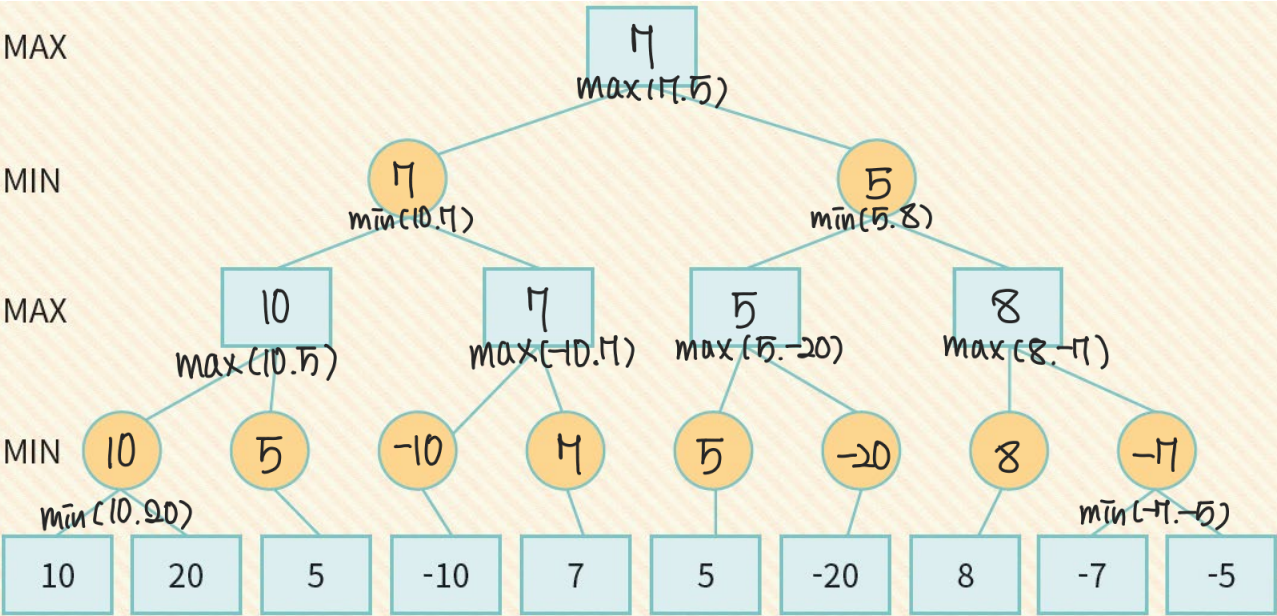
Minimax algorithm 성능의 분석

완결성(completeness) : 유한한 탐색 트리 안에 해답이 존재하면, 반드시 찾을 수 있음.
최적성(optimality) : 최적의 알고리즘
시간 복잡도(time complexity) : 시간복잡도가 아주 높으며, 실제 게임에서 이 알고리즘을 변경없이 적용하는 것은 비현실적
=이 부분을 보완하기 위해 알파베타 가지치기(Alpha-Beta Pruning)가 나옴
공간 복잡도(space complexity) : 시간 복잡도와 마찬가지로 높음.

3. 알파베타 가지치기(Alpha-Beta Pruning)

알파베타 가지치기(Alpha-Beta Pruning)
: 탐색 트리의 어떤 부분은 제외하여도 결과에 영향을 주지 않는다는 것을 발견하였고, 탐색 범위를 가지치기하여 줄인다.
(모든 노드를 조사하지 않고, 시간 복잡도를 줄일 수 있음)

탐색을 할 때 alpha값, beta값이 자식 노드로 전달
MAX는 alpha에 업데이트, MIN은 beta에 업데이트
자식 노드 검사 후 부모 노드로 업데이트 할 때, 자식 노드 안의 값만이 업데이트
Alpha-beta Pruning condition 의 경우, 가지치기
=다음 조건을 만족할 때는 뒤의 노드를 검사하지 않아도 결과에 영향을 주지 않기에, 가지치기를 하여 시간복잡도를 줄이고, 검사한 노드만 부모 노드로 업데이트 된다.

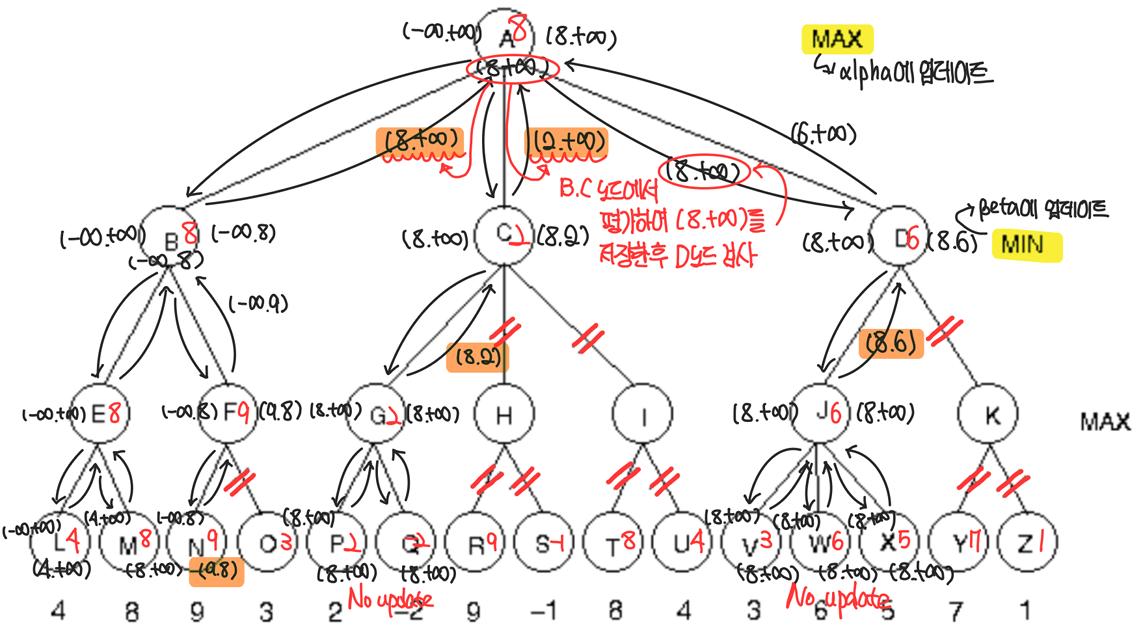
Alpha-beta Pruning Example 1

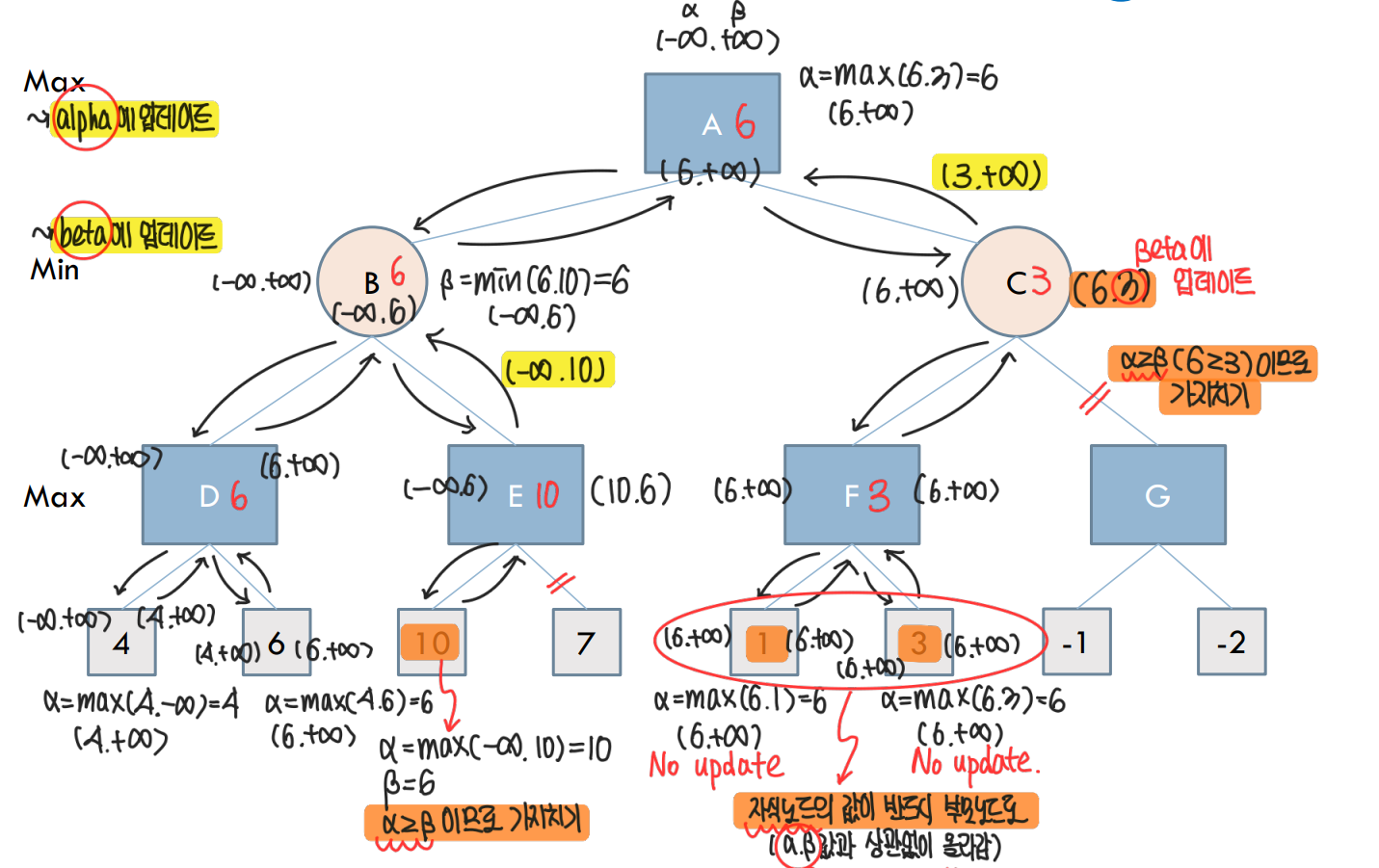
Alpha-beta Pruning Example 2

예제 출처

Alpha-beta Pruning Example 3

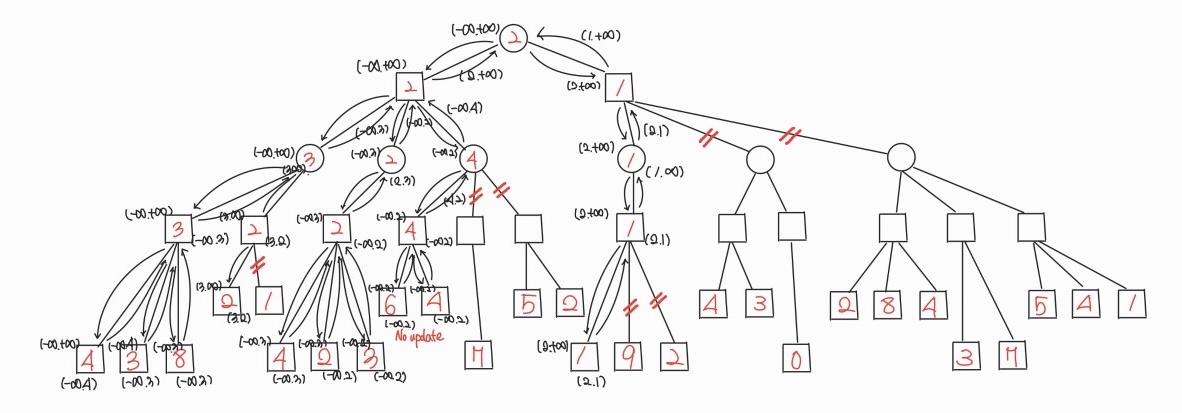
가지치기할 때 주의할 점

범위가 내려올 때와 올라올 때를 잘 확인하기 (처음에는 괜찮지만 뒤로 갈 수록 저장된 범위가 복잡함)
MAX, MIN 구분 잘 하기 (알파, 베타 업데이트가 틀려지기 때문)

4. Game Tree 실습

Minimax Algorithm python code / Alpha-beta Pruning code

Minimax Algorithm python code

# 보드는 1차원 리스트로 구현한다.
game_board = [' ', ' ', ' ',
              ' ', ' ', ' ',
              ' ', ' ', ' ']

# 비어있는 칸을 찾아서 리스트로 반환한다.
def empty_cells(board):
    cells = []
    for x, cell in enumerate(board):
        if cell == ' ':
            cells.append(x)
    return cells

# 비어있는 칸에는 놓을 수 있다.
def valid_move(x):
    return x in empty_cells(game_board)

# 위치 x에 놓는다.
def move(x, player):
    if valid_move(x):
        game_board[x] = player
        return True
    return False

# 현재 게임 보드를 그린다.
def draw(board):
    for i, cell in enumerate(board):
        if i % 3 == 0:
            print('\n---------------')
        print('|', cell, '|', end='')
    print('\n---------------')

# 보드의 상태를 평가한다.
def evaluate(board):
    if check_win(board, 'X'):
        score = 1
    elif check_win(board, 'O'):
        score = -1
    else:
        score = 0
    return score

# 1차원 리스트에서 동일한 문자가 수직선이나 수평선, 대각선으로 나타나면 승리한 것으로 한다.
def check_win(board, player):
    win_conf = [
        [board[0], board[1], board[2]],
        [board[3], board[4], board[5]],
        [board[6], board[7], board[8]],
        [board[0], board[3], board[6]],
        [board[1], board[4], board[7]],
        [board[2], board[5], board[8]],
        [board[0], board[4], board[8]],
        [board[2], board[4], board[6]],
    ]
    return [player, player, player] in win_conf

# 1차원 리스트에서 동일한 문자가 수직선이나 수평선, 대각선으로 나타나면 승리한 것으로 한다.
def game_over(board):
    return check_win(board, 'X') or check_win(board, 'O')

# 미니맥스 알고리즘을 구현한다.
# 이 함수는 순환적으로 호출된다.
def minimax(board, depth, maxPlayer):
    pos = -1
    # 단말 노드이면 보드를 평가하여 위치와 평가값을 반환한다.
    if depth == 0 or len(empty_cells(board)) == 0 or game_over(board):
        return -1, evaluate(board)

    if maxPlayer:
        value = -10000   # 음의 무한대
        # 자식 노드를 하나씩 평가하여서 최선의 수를 찾는다
        for p in empty_cells(board):
            board[p] = 'X'

            # 경기자를 교체하여서 minimax()를 순환호출한다.
            x, score = minimax(board, depth - 1, False)
            board[p] = ' '
            if score > value:
                value = score
                pos = p


    else:
        value = 10000  # 양의 무한대
        # 자식 노드를 하나씩 평가하여서 최선의 수를 찾는다.
        for p in empty_cells(board):
            board[p] = 'O'

            # 경기자를 교체하여서 minimax()를 순환호출한다.
            x, score = minimax(board, depth - 1, True)
            board[p] = ' '
            if score < value:
                value = score
                pos = p
    return pos, value

player = 'X'

# 메인 프로그램
while True:
    draw(game_board)
    if len(empty_cells(game_board)) == 0 or game_over(game_board):
        break
    i, v = minimax(game_board, 9, player == 'X')
    move(i, player)
    if player == 'X':
        player = 'O'
    else:
        player = 'X'

if check_win(game_board, 'X'):
    print("X 승리!")
elif check_win(game_board, 'O'):
    print("O 승리!")
else:
    print('비겼습니다')

Alpha-beta Pruning python code

# 보드는 1차원 리스트로 구현한다.
game_board = [' ', ' ', ' ',
              ' ', ' ', ' ',
              ' ', ' ', ' ']

# 비어있는 칸을 찾아서 리스트로 반환한다.
def empty_cells(board):
    cells = []
    for x, cell in enumerate(board):
        if cell == ' ':
            cells.append(x)
    return cells

# 비어있는 칸에는 놓을 수 있다.
def valid_move(x):
    return x in empty_cells(game_board)

# 위치 x에 놓는다.
def move(x, player):
    if valid_move(x):
        game_board[x] = player
        return True
    return False

# 현재 게임 보드를 그린다.
def draw(board):
    for i, cell in enumerate(board):
        if i % 3 == 0:
            print('\n---------------')
        print('|', cell, '|', end='')
    print('\n---------------')

# 보드의 상태를 평가한다.
def evaluate(board):
    if check_win(board, 'X'):
        score = 1
    elif check_win(board, 'O'):
        score = -1
    else:
        score = 0
    return score

# 1차원 리스트에서 동일한 문자가 수직선이나 수평선, 대각선으로 나타나면 승리한 것으로 한다.
def check_win(board, player):
    win_conf = [
        [board[0], board[1], board[2]],
        [board[3], board[4], board[5]],
        [board[6], board[7], board[8]],
        [board[0], board[3], board[6]],
        [board[1], board[4], board[7]],
        [board[2], board[5], board[8]],
        [board[0], board[4], board[8]],
        [board[2], board[4], board[6]],
    ]
    return [player, player, player] in win_conf

# 1차원 리스트에서 동일한 문자가 수직선이나 수평선, 대각선으로 나타나면 승리한 것으로 한다.
def game_over(board):
    return check_win(board, 'X') or check_win(board, 'O')

# 미니맥스 알고리즘을 구현한다.
# 이 함수는 순환적으로 호출된다.
def minimax(board, depth, maxPlayer, alpha, beta):
    pos = -1
    # 단말 노드이면 보드를 평가하여 위치와 평가값을 반환한다.
    if depth == 0 or len(empty_cells(board)) == 0 or game_over(board):
        return -1, evaluate(board)

    if maxPlayer:
        value = -10000  # 음의 무한대
        for p in empty_cells(board):
            board[p] = 'X'
            x, score = minimax(board, depth - 1, False, alpha, beta)
            board[p] = ' '
            if score > value:
                value = score
                pos = p
            alpha = max(alpha, value)
            if alpha >= beta:  # 알파베타 프루닝 조건
                break
    else:
        value = 10000  # 양의 무한대
        for p in empty_cells(board):
            board[p] = 'O'
            x, score = minimax(board, depth - 1, True, alpha, beta)
            board[p] = ' '
            if score < value:
                value = score
                pos = p
            beta = min(beta, value)
            if beta <= alpha:  # 알파베타 프루닝 조건
                break

    return pos, value

player = 'X'  # 초기화

# 메인 프로그램
while True:
    draw(game_board)
    if len(empty_cells(game_board)) == 0 or game_over(game_board):
        break
    i, v = minimax(game_board, 9, player == 'X', -10000, 10000)
    move(i, player)
    if player == 'X':
        player = 'O'
    else:
        player = 'X'

if check_win(game_board, 'X'):
    print("X 승리!")
elif check_win(game_board, 'O'):
    print("O 승리!")
else:
    print('비겼습니다')

Alpha-Beta Pruning code 참고

5. 휴리스틱 평가 함수(evaluation function) | 불완전한 결정

미니맥스 알고리즘은 탐색 공간 전체를 탐색하는 것을 가정하는데, 게임을 하는 상황에는 적당한 시간 안에 다음 수를 결정하여야 한다.
이때는 탐색을 끝내야 하는 시간에 도달하면 탐색을 중단하고 휴리스틱 평가 함수(evaluation function)를 적용해야 한다.

평가 함수는 경험적 방법에 의존하여 설계해야 한다.