Sequential Data

: 특정 순서를 가지는 데이터(ex. 쇼핑몰 구매 목록, 유전자 서열, 주식)

1. Forcasting Problem

N discrete states 중 하나의 상태를 갖는 시스템 $q_t$
(정의된 상태는 랜덤으로 변하는 stochastic systems)

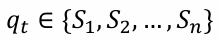
과거의 모든 상태를 구하는 것은 거의 불가능 하다
(현재 state( $S_t$ )의 모든 과거에 대하여 ( $S_1, S_2, S_3, ...$ ) 계산하기가 힘들다는 뜻

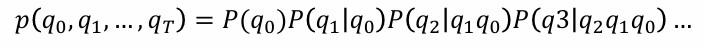
2. Markov Process

Markov Property

: 미래의 상태는 오직 현재 상태에만 영향을 받는다
(바로 직전의 정보가 과거의 정보를 담고 있다고 가정)
(모든 과거를 취급하면 계산이 힘들다는 Forcasting Problem을 해결)

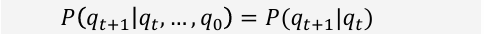
Markov Process

랜덤 프로세스이며 확률적인 행동을 표현하고, 연속적인 행동의 변화를 관찰한다.

• a finite set of $N$ states, $S = { S_1, ..., S_N }$
• a state transition probability
• an initial state probability distribution
  

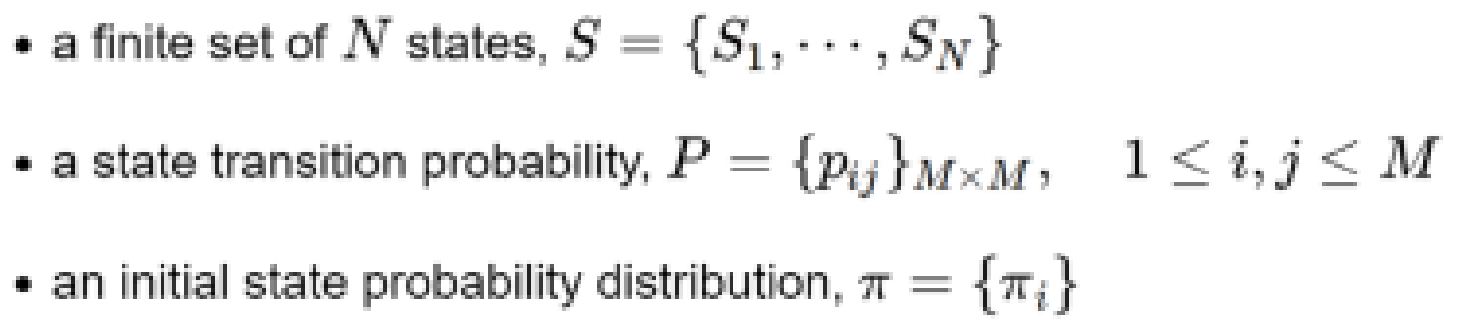
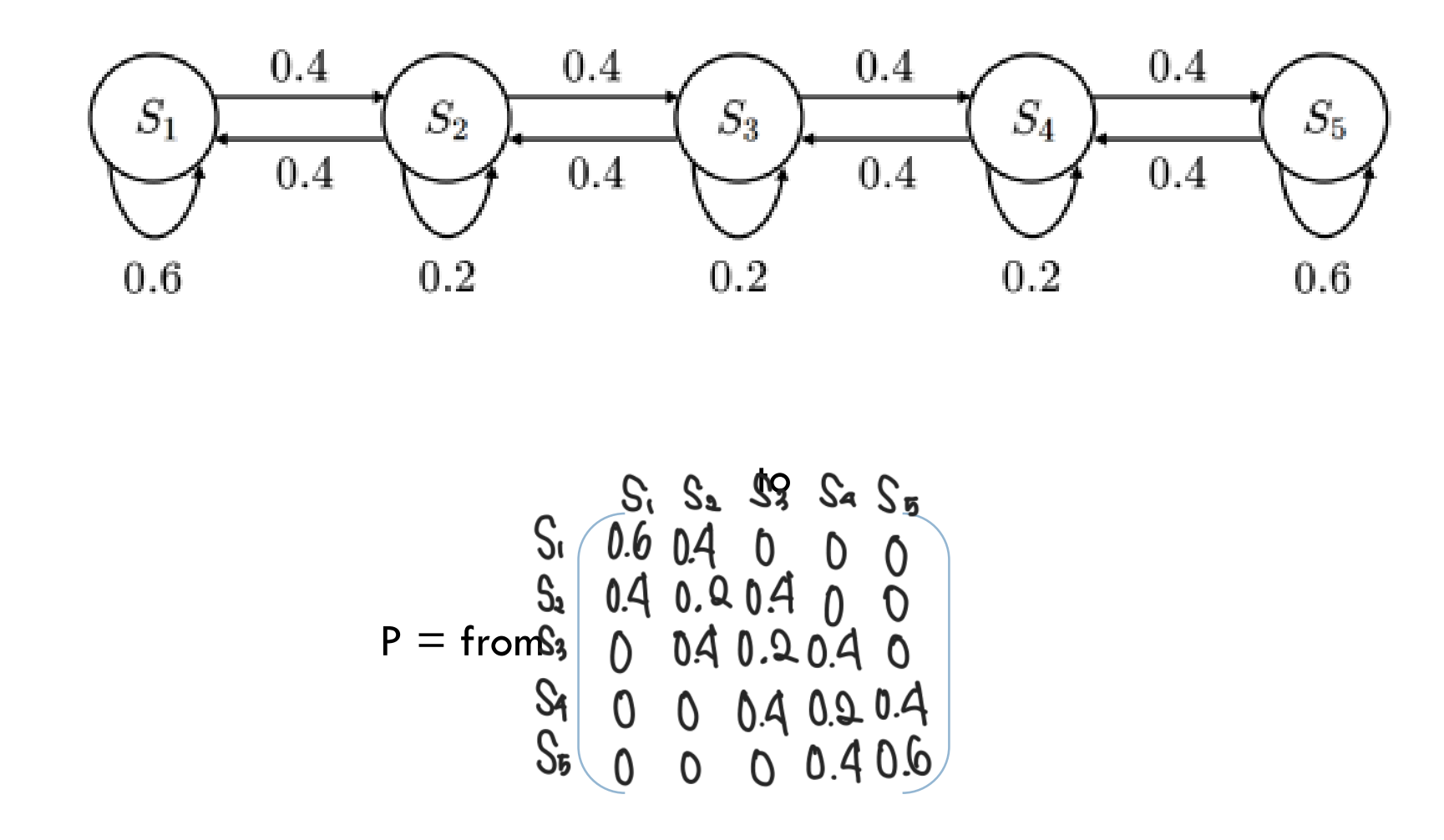
3. State Transition Matrix

: Markov Process의 요소 중 하나로, 상대 변화 확률의 행렬

state transition probability

$s$와 성공 상태 $s’$(다음 상태)에 대한 상태 변화 확률
(조건부 확률로써, $S_t$가 주어졌을 때 (is given)를 나타낸 표현)

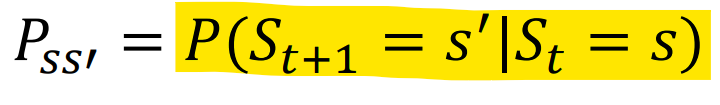
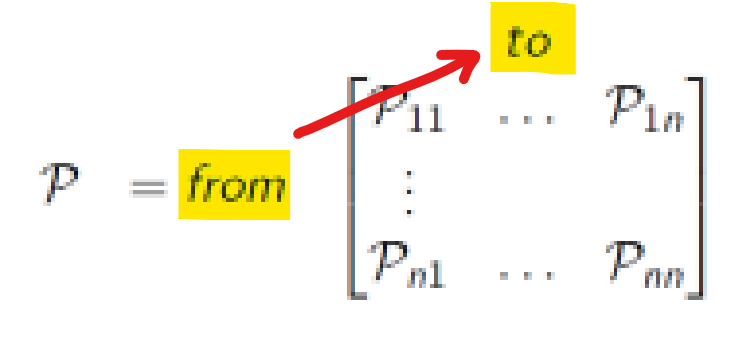
State Transition Matrix

P는 모든 상태 $s$로부터 다음 상태로 $s’$로 변할 확률을 나타낸 행렬
(->State Transition Matrix의 각 행 합은 1이다)

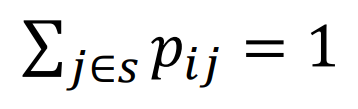
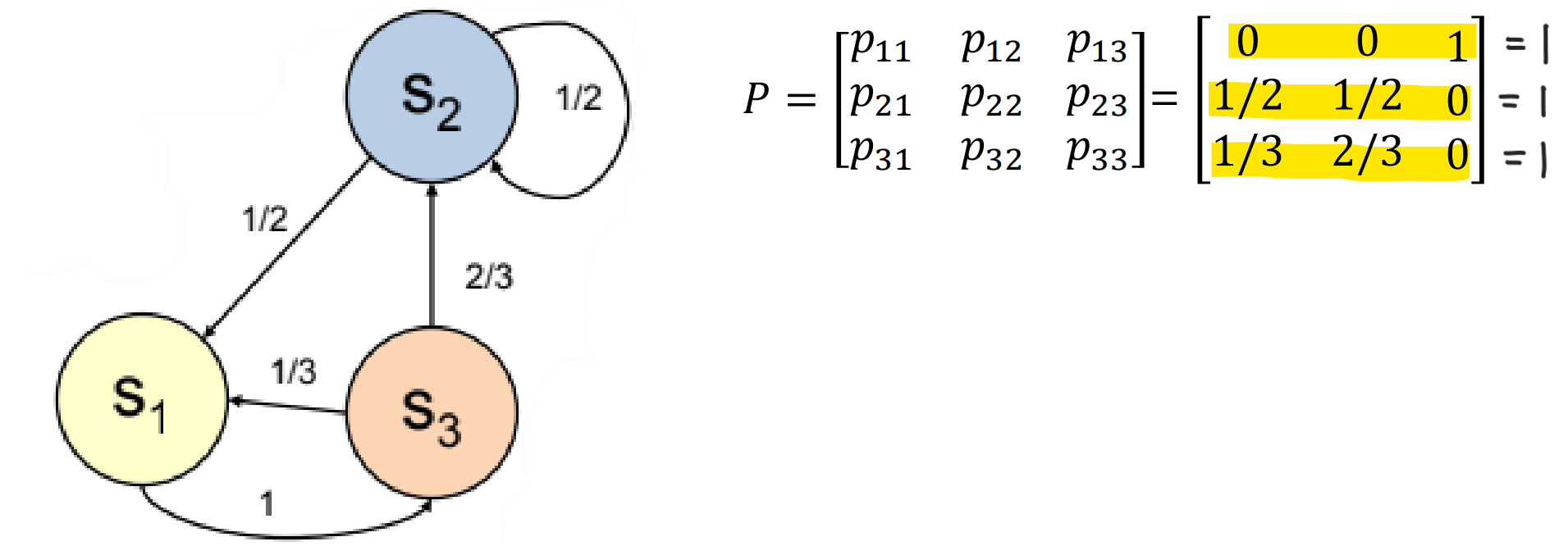
Example 1. MP Model State Transition Matrix

Example 2. MP Model State Transition Matrix

4. Hidden Markov Model

같은 시간에 발생한 두 종류의 state sequence 각각의 특성과 그들의 관계를 모델링

• Hidden state sequence(Type 1) : 관측이 되어지지 않고 숨겨져 있는 것
• Observable state sequence(Type 2) : 관측이 가능한 것
  
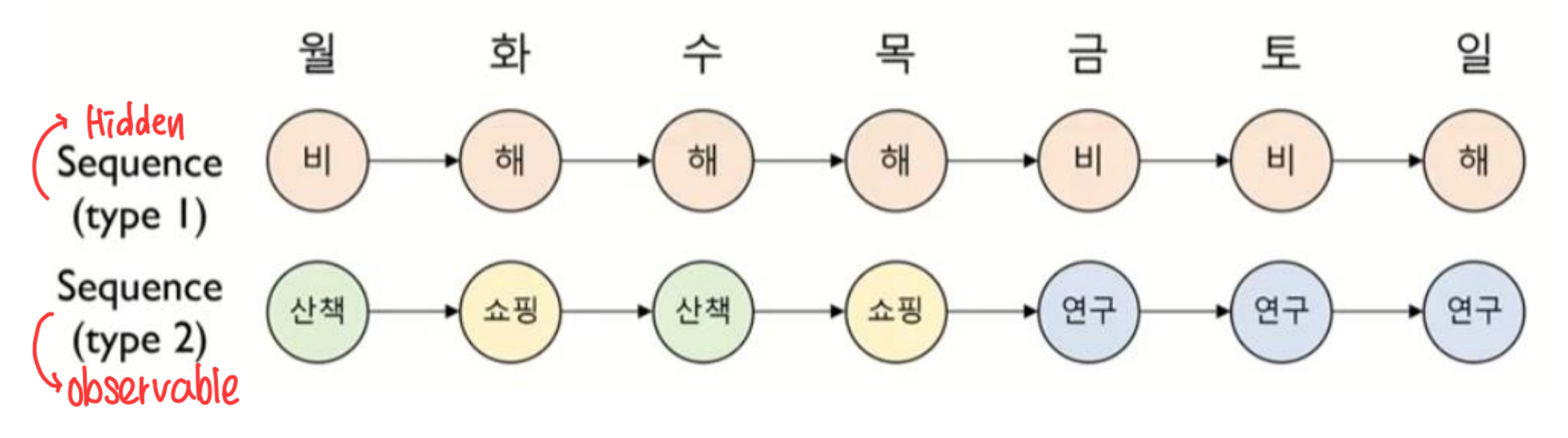
  Hidden sequence 가 Markov assumption을 따름 -> 순차적 특성을 반영
  Observable sequence 는 순차적 특정을 반영하는 Hidden state에 종속 (이부분은 밑에 그래프를 보면 이해가 쉬움)

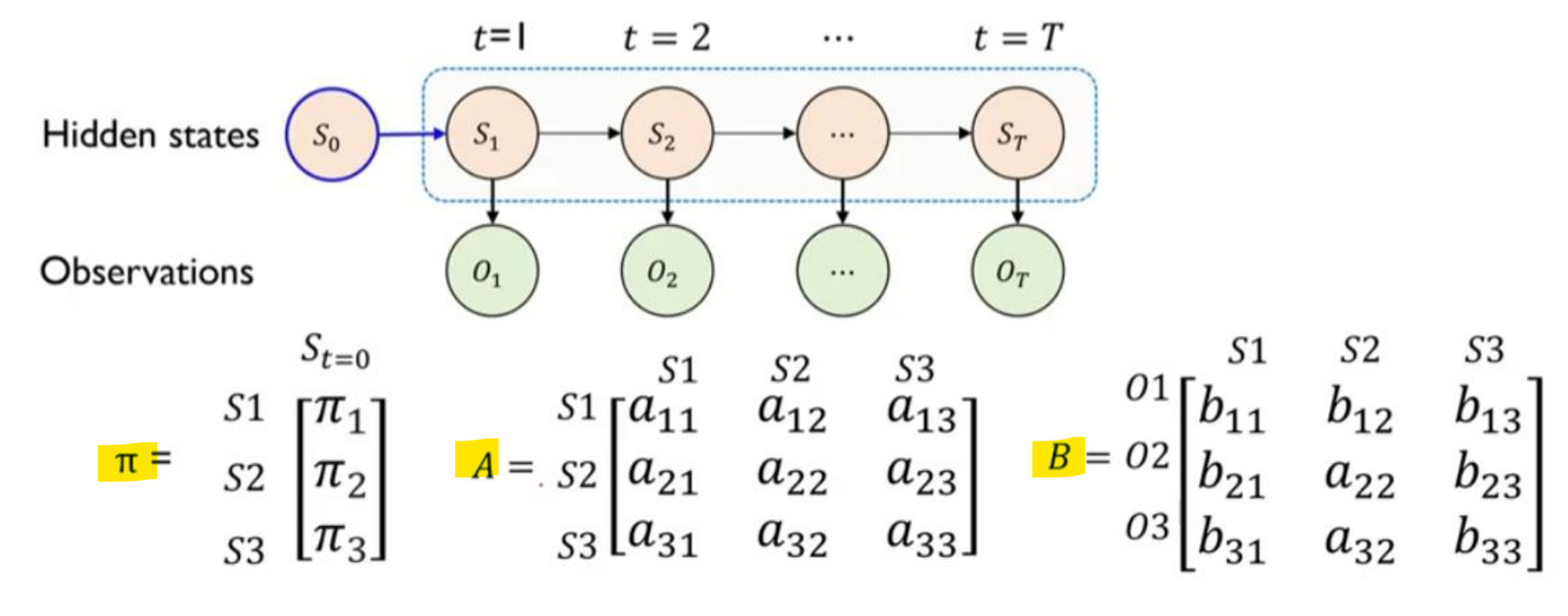
Parameters of a Hidden Markov Model : 𝝀 = { 𝑨, 𝑩, 𝝅 }

상태전이 확률 (State transition probability), 𝑨 : HMM이 작동하는 도중 다음 상태를 결정
방출 확률 (Emission probability), 𝑩 : HMM이 어느 상태에 도달했을 때, 그 상태에서 관측될 확률 결정
초기 상태 확률 (Initial State Probability), 𝝅 : HMM을 가동시킬 때 어느 상태에서 시작할 지 결정 (제일 처음에 어디서부터 시작하는지)

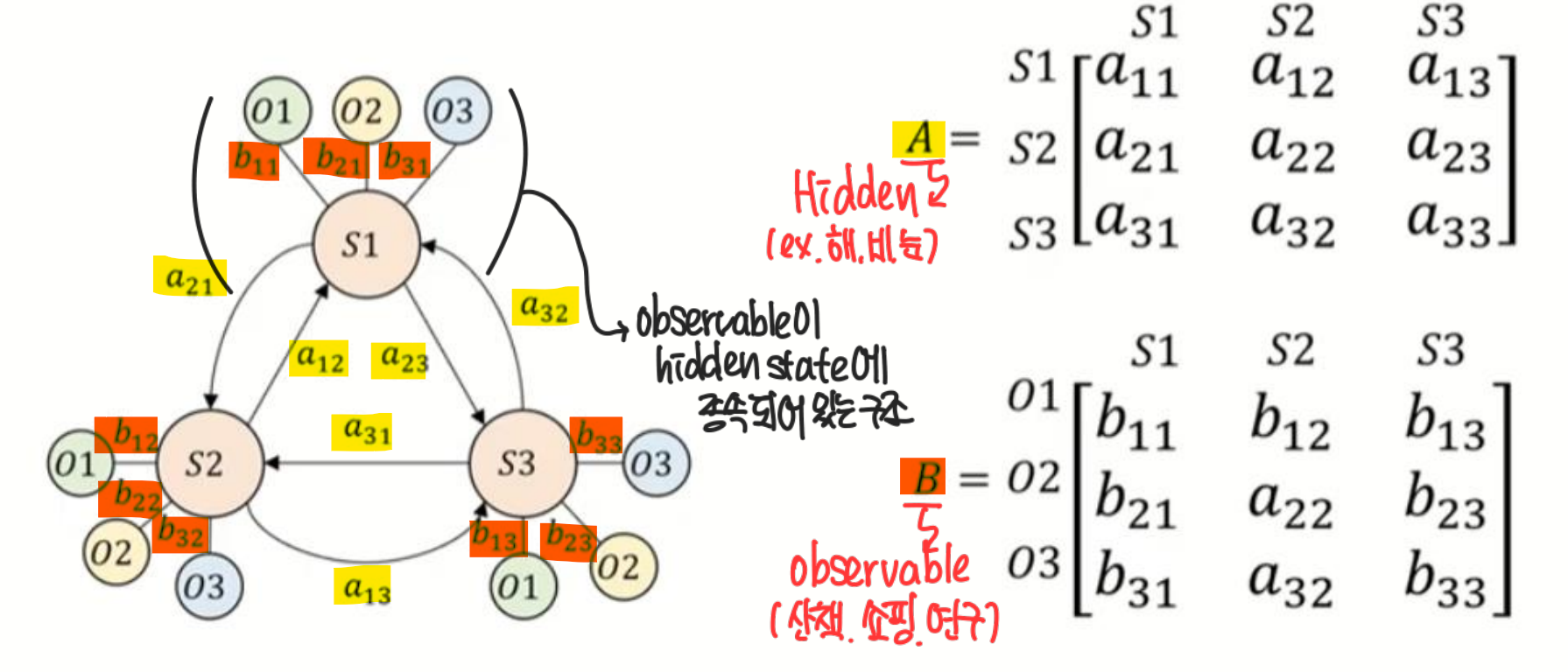
(자세히 보면 그래프 상태 전이 확률 방향이 틀렸음.)

HMM Problems (문제 유형)

• Evaluation problem: HMM(𝜆∗)과 O가 주어졌을 때 Observable sequence O’의 확률
• Decoding problem: HMM(𝜆∗)과 O가 주어졌을 때 hidden state sequence를 찾는 문제
• Learning problem: $X={𝑂_1, . .𝑂_𝑁}$ 이 주어졌을 때 HMM(𝜆∗) 을 찾는 문제

5. 실습

: Evaluation problem과 Decoding problem 문제 풀기

Evaluation problem

HMM(𝜆∗)과 O가 주어졌을 때 Observable sequence O’의 확률
Solution: Forward algorithm (or Backward algorithm, 수업 안 함)
(만약 전방 확률(Forward probability)을 사용하지 않는다면, 총 상태의 개수 $N$과 Sequence의 길이 $T$에 따라 총 $N^T$의 경우의 수를 계산해야 한다)

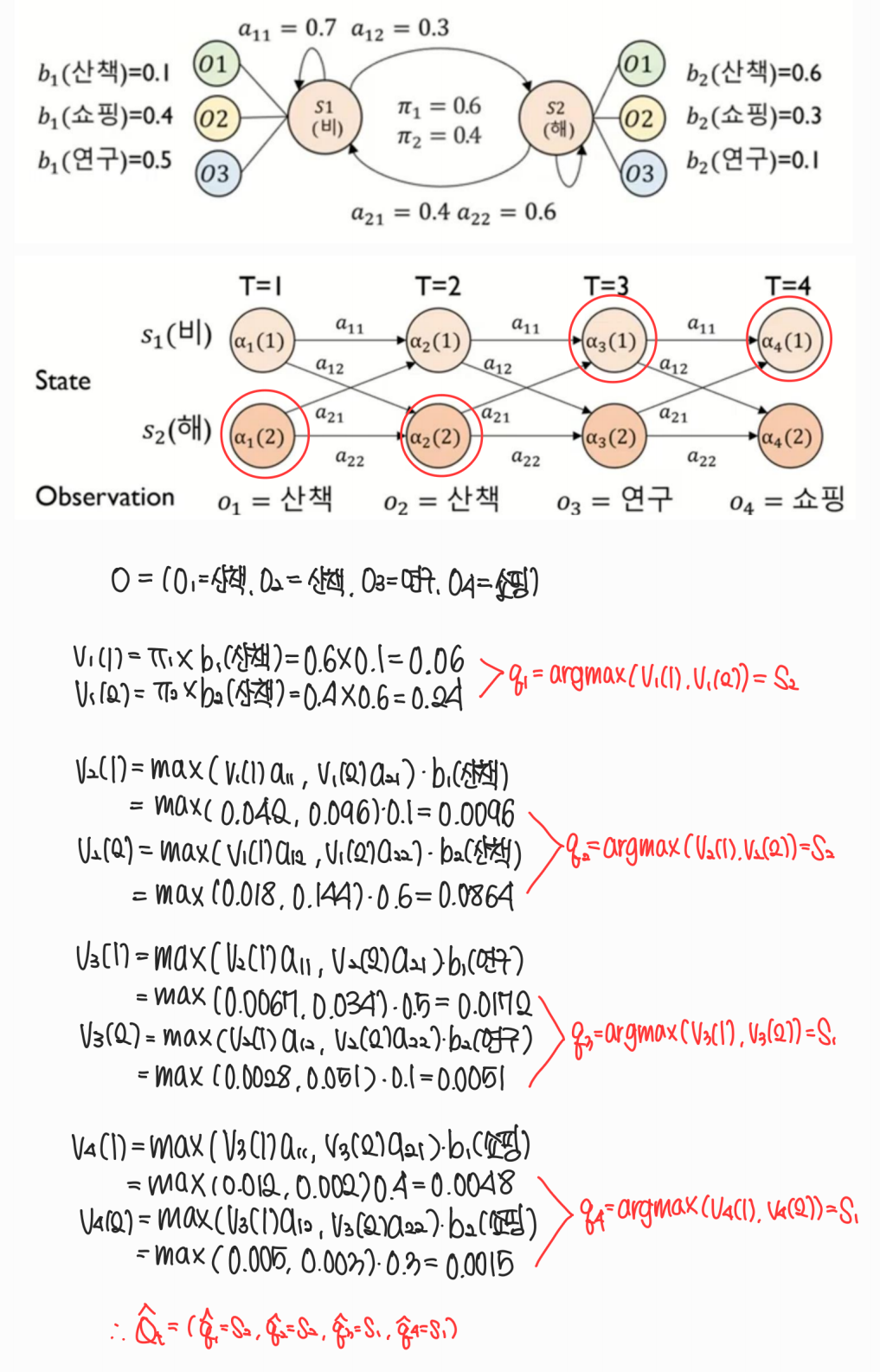
Example : 오늘 산책, 내일 산책, 모레 연구, 글피 쇼핑할 확률은?

Forward probability는 주어진 Sequence O 가 HMM에 속할 확률 문제에 활용 가능
(HMM1과 HMM2가 있을 때 어느 HMM에 속할 확률이 높을지? -> Sequence classification 문제에 활용 가능)

---

Decoding problem (HMM의 핵심)

HMM(𝜆∗)과 O가 주어졌을 때 최적의 hidden state sequence를 찾는 문제
Solution: Viterbi Algorithm

( $max$ : 최댓값 / $argmax$ : 최댓값의 인덱스)

Example: 오늘 산책, 내일 산책, 모레 연구, 글피 쇼핑을 했다면 각 날들 날씨는?

---

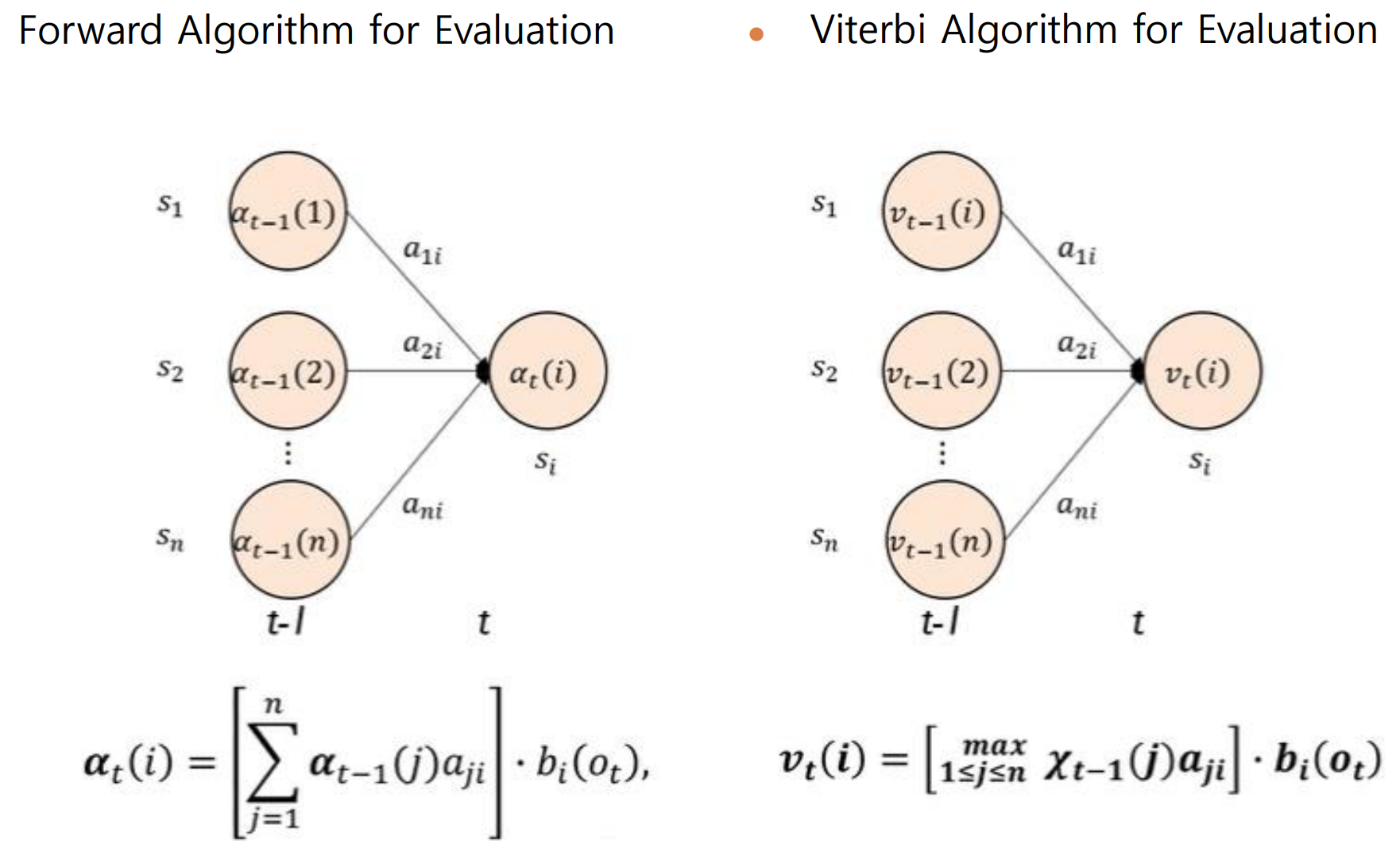
Evaluation vs. Decoding

• Forward Algorithm for Evaluation : 가능한 모든 경우의 확률 합 (Observable state의 확률을 구하는 것이 목표)
• 가능한 모든 경우의 확률 최대 (가장 최적의 상태를 찾는 것)

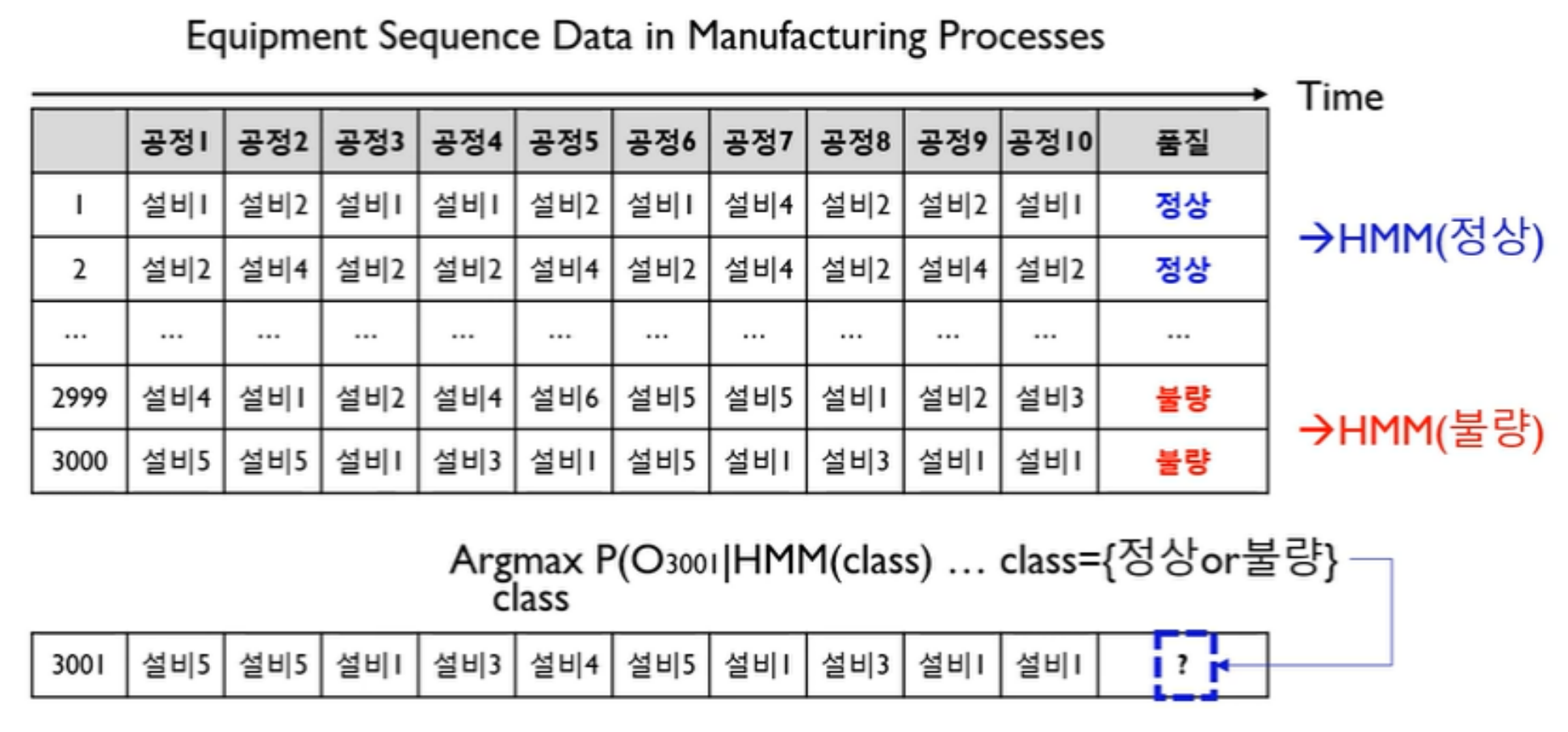
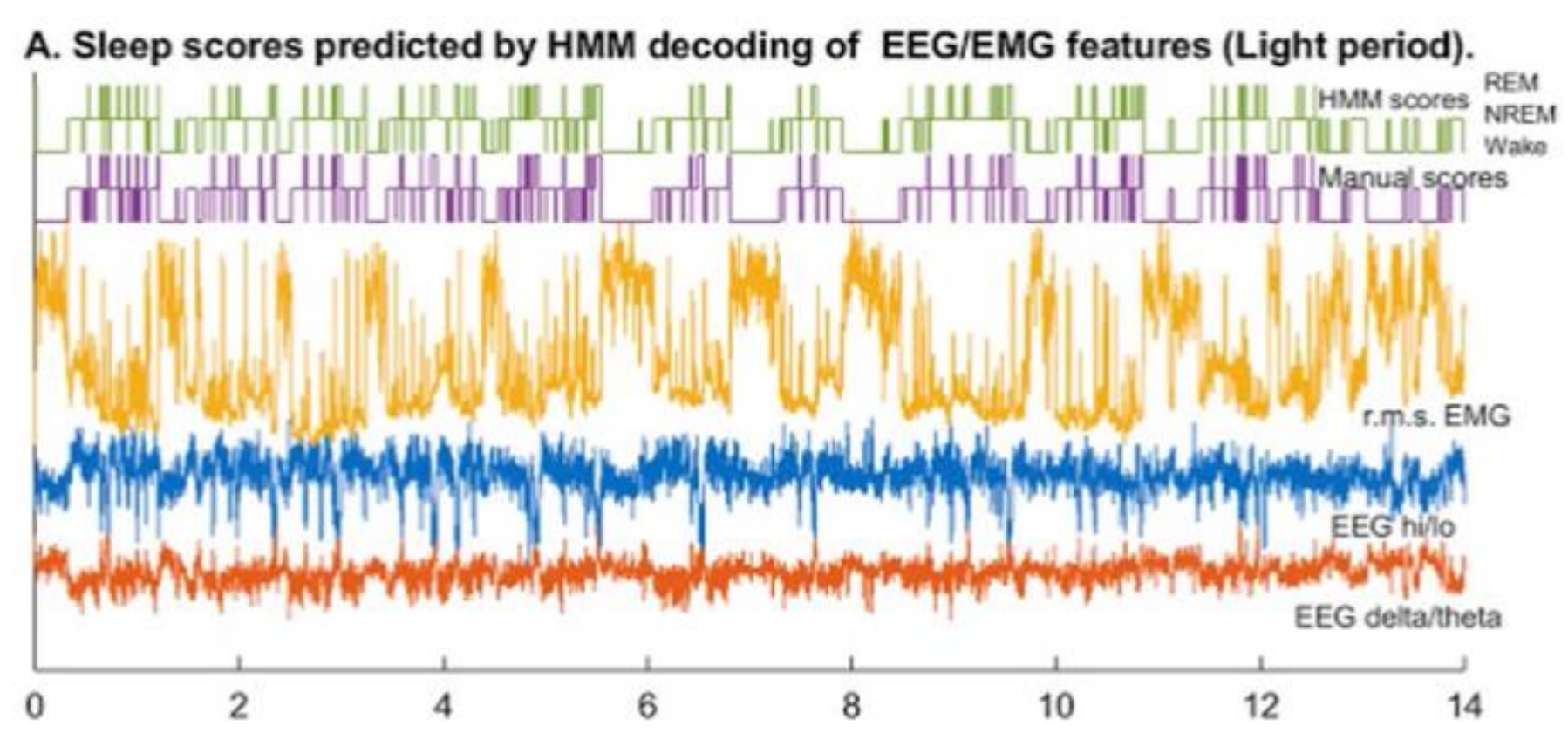
HMM 실생활 응용

• HMM Evaluation Application
  관측 시퀀스 : 설비 ID 데이터 / 은닉 시퀀스 : 공정 ID 데이터
  
• HMM Decoding Application
  관측 시퀀스 : 수면 EEG 데이터 / 은닉 시퀀스 : REM-수면, NREM-수면, wake