1. 탐색(search)

탐색 : 컴퓨터가 문제를 해결하기 위하여 스스로 해답에 이르는 경로
상태공간(state) : 상태들이 모여있는 공간
초기 상태(initial state) : 문제해결을 시작하는 상태
목표 상태(goal state) : 목표가 되는 상태

2. 상태 공간 탐색 문제

경로 발견 문제 : 목표 상태가 주어지고, 경로(path)를 발견하는 문제(ex. 8-puzzle, 지도에서의 경로 발견)
목표 상태 발견 문제 : 목표 상태만 발견하면 되는 문제(경로는 X) (ex. N-queen)

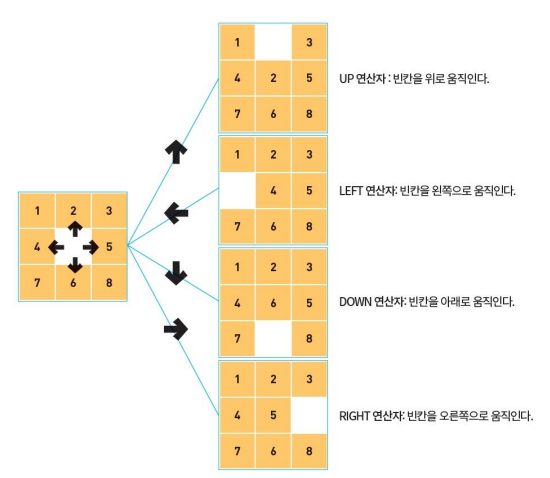
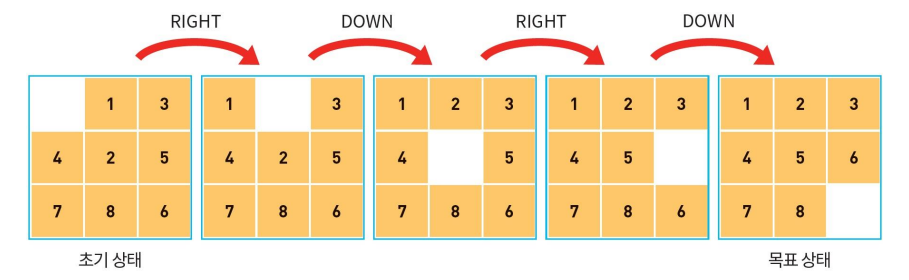
Example 1. 경로 발견 문제 8-puzzle

(반칸을 기준으로 up, left, down, right가 이루어진다. 헷갈리지 말도록 하자)
초기 상태에서 목표 상태를 발견하는 것만이 아니라, 경로(right, down, right, down)도 또한 탐색하게 된다.

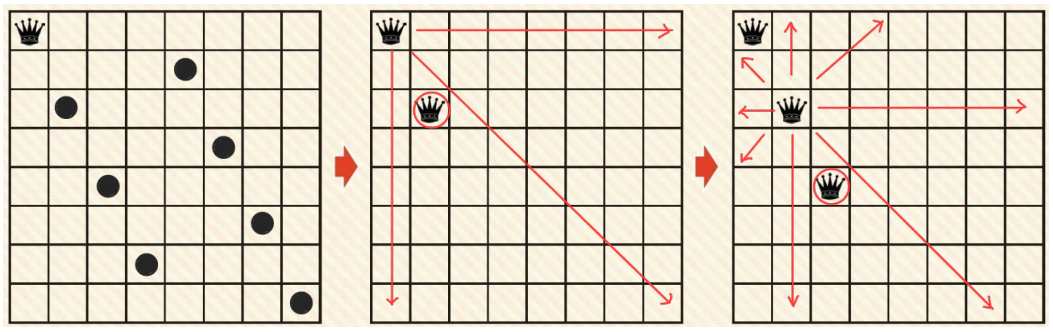
Example 2. 목표 상태 발견 문제 N-queen

N-queen RULE

• 각각을 정해진 열에서만 움직이게 한다. (일반적으로는 왼쪽>오른쪽)
• 퀸이 움직일 수 있는 오른쪽/왼쪽/대각선쪽 에는 또 다른 퀸이 와서는 안 된다.

연산자 집합 $O=${ $place_i | 1 \le i \le 8$ }

3. 탐색 트리(search tree)

탐색트리 과정에 있어서 필요한 개념 정리

노드(node) : 상태
간선(edge) : 연산자, 노드를 연결하는 선
루트 노드(root node) : 초기 상태
단말 노드(leaf node) : 자식이 없는 node
=아래 사진을 기준으로 leaf node는 3, 6, 19 (노란색으로 표기된 곳) 이다.
형제 노드(siblings node) : 같은 부모를 가지는 node
노드의 깊이(depth): 루트노드에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수

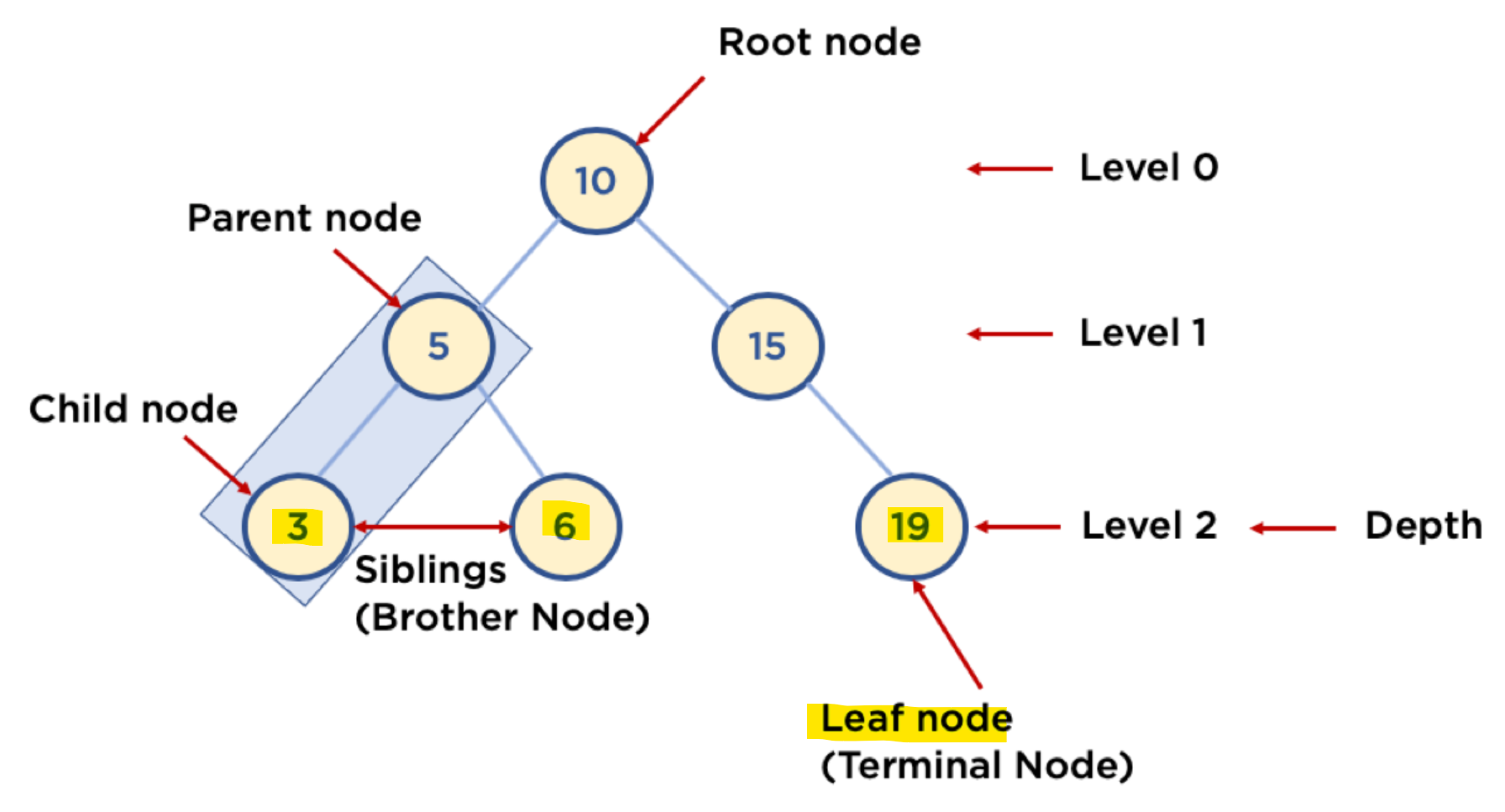
• 위의 사진을 기준으로 탐색트리의 특징을 정리할 수 있다.
  한 개의 루트 노드만이 존재하며, 자식노드들은 한 개의 부모노드 만을 가진다.
  연산자를 적용하기 전 까지 탐색 트리는 미리 만들어져 있지 않는다.

4-queen 문제 탐색 트리

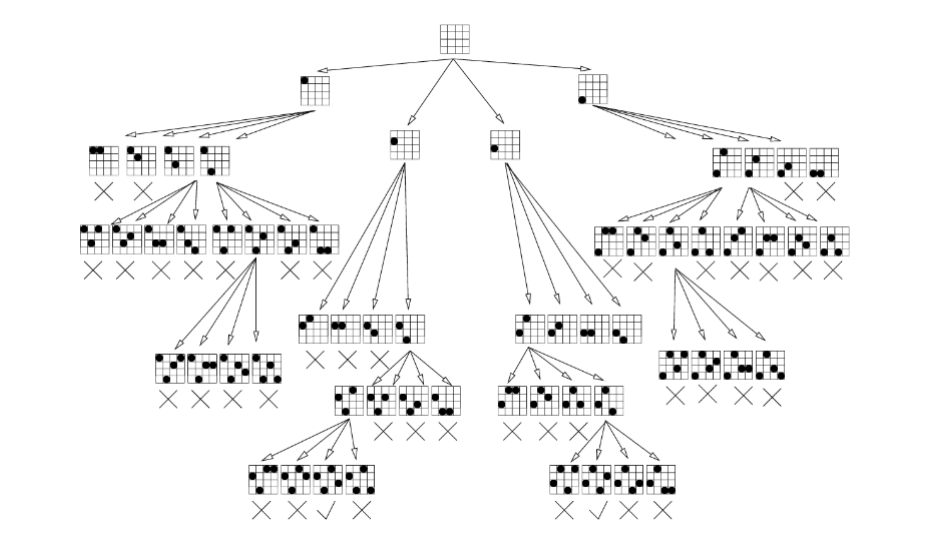
확장된 상태 중 4-queen 문제에 어긋나는 상태는 더 이상 확장하지 않고 멈추는 것을 확인할 수 있다.
불필요한 경우를 제외하고 탐색하여, 효율적으로 계산할 수 있게 된다.

---

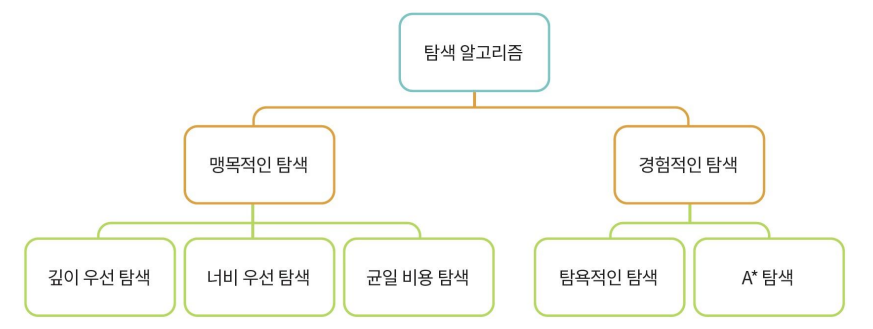
기본적인 탐색 기법

맹목적인 탐색 방법(blind search method) : 목표 노드에 대한 정보를 이용하지 않고, 기계적인 탐색으로 매우 소모적인 탐색을 하게된다. 노드를 확장하는 순서가 달라지는 경우가 많다. (ex. DFS-BFS) (uninformed search 라고도 한다)
경험적 탐색 방법(heuristic search method) : 목표 노드에 대한 경험적인 정보를 사용하는 방법이고, 효율적인 탐색이 가능하다. 이런 경험적 정보를 휴리스틱(heuristic)이라고 한다.

탐색기법마다 개념이 많아 각자 정리한다. 순서대로 맹목적인 탐색(깊이/너비/균일비용) 경험적인 탐색(탐욕/A)로 정리하겠다.
그 전에 DFS와 BFS를 공부하기 위해, open list와 closed list를 알아보겠다.
open list(frontier) : 확장은 되었으나 아직 탐색하지 상태들이 있는 리스트
closed list(reached) : 탐색이 끝난 상태들이 들어있는 리스트
(list는 순서가 정해져 있다는 것이 DFS와 BFS에서 중요하게 작용)

탐색 성능 측정

완결성(completeness) : 문제에 해답이 있다면, 반드시 해답을 찾을 수 있는지 여부
최적성(optimality) : 가장 비용이 낮은 해답을 찾을 수 있는지 여부
시간 복잡도(time complexity) : 해답을 찾는데 걸리는 시간
공간 복잡도(space complexity) : 탐색을 수행하는데 필요한 메모리의 양

시간과 공간 복잡도는 다음과 같은 기호로 측정
b : 탐색 트리의 최대 분기 개수
d : 목표 노드의 깊이
m : 트리의 최대 깊이

---

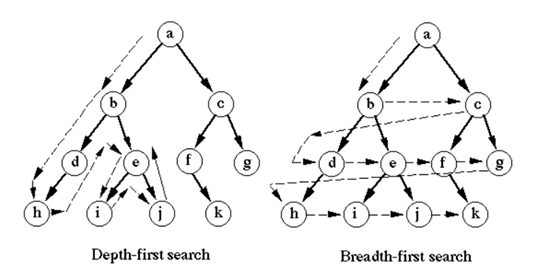
4. DFS : Depth-First Search (깊이 우선 탐색)

탐색 트리 상에서 해가 존재할 가능성이 있는 한, (왼쪽으로) 계속 전진하여 탐색하는 방법이다.
더이상 진행할 경로가 없을 때, 이전 상태 중 다른 경로로 갈 수 있는 위치로 복귀하여 탐색을 계속한다.
쉽게 말하면, 왼쪽으로 인접한 노드가 없을 때까지 (가장 깊은 노드) 탐색한 뒤 되돌아가 탐색을 하는 방식
(설명으로 이해하려면 까다롭기에 그림 혹은 예제를 이용하여 푸는 것이 효과적이다)
DFS 사진출처

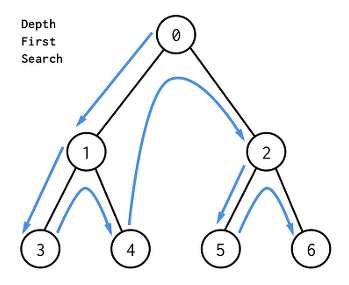
DFS 탐색의 진행

1. 각 반복 때마다 상태 S의 모든 자식 노드를 생성하고, 이들은 open list 에 추가한다.
   =이때 list의 처음에 추가한다(LIFO(Last in-Fist out) 데이터 구조로 유지)
   =가장 최근에 open list에 들어간 상태가 먼저 나가게 된다.
2. open list와 closed list는 결국 list이므로 순서가 정해져있다. (알파벳 순서대로 임의로 작성 X)

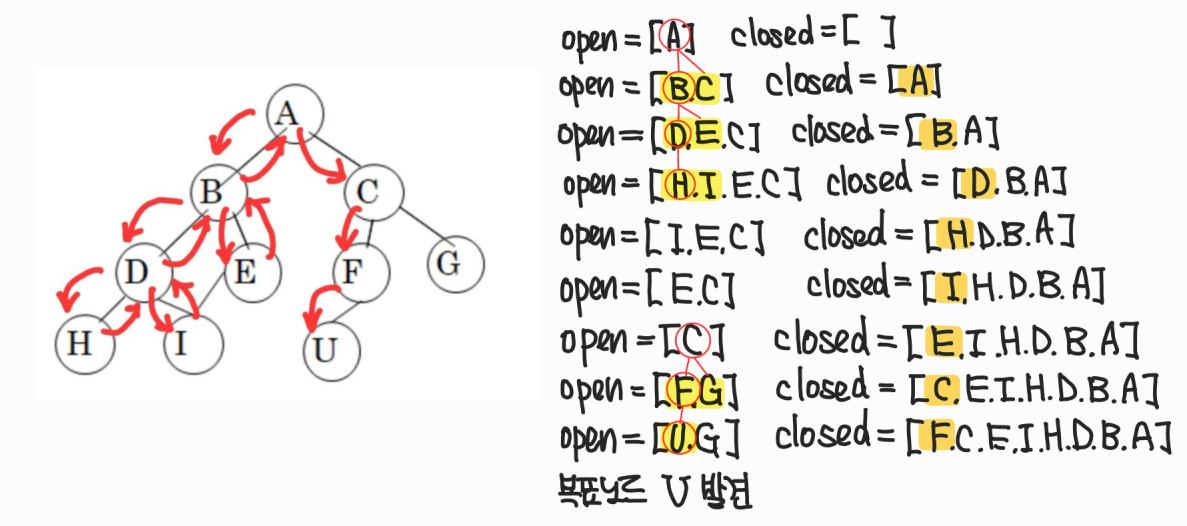
DFS 탐색시 open list와 closed list

DFS는 LIFO 구조로 open list에서 자식 노드가 insert(0,state)로 먼저 삽입된다.
open list의 순서를 작성할 때는 검사하는 상태가 뭔지를 확인하며, 그 자식 노드를 리스트의 앞에서 왼쪽 순서대로 작성해야 한다.
(노란색 형광펜 참고)
closed list를 작성할 때는 검사된 것을 추가하고, 순서는 그 코드에서 append()를 쓰면 뒤로, insert(0,state)를 쓰면 앞으로 작성하면 된다.
(->open list의 순서는 중요하지만 closed list의 순서는 크게 상관없으므로 쓰여진 코드에 따라 작성)

DFS 전체 소스 코드 분석(8-puzzle)

DFS 성능의 분석

• 완결성(completeness) : 무한 경로를 따라 끝 없이 나아갈 수도 있음. 따라서 무한 공간에서는 완결적 X

• 최적성(optimality) : 가장 경로가 짧은 최적의 해답은 발견 X. 가장 왼쪽에 있는 해답만을 발견

• 시간 복잡도(time complexity) : 만약 m(트리의 최대 깊이)가 d(정답의 깊이) 보다 아주 크다면 시간이 많이 걸림. 하지만 그렇지 않은 경우라면, BFS(너비우선 탐색) 보다 더 빠름.

• 공간 복잡도(space complexity) : 선형 복잡도만을 가지고, 탐색 트리에서 한 줄 단위로 탐색하므로 모든 노드를 저장하고 있지 않음. BFS(너비 우선 탐색)에 비하여 큰 장점.

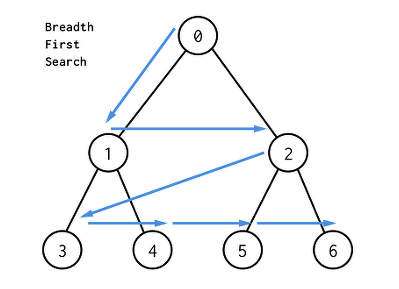
5. BFS : Breadth-First Search (너비 우선 탐색)

루트 노드의 모든 자식 노드들을 왼쪽부터 탐색한 후에 해가 발견되지 않으면 한 레벨 내려가서 동일한 방법으로 탐색하는 방법이다.
목표 노트를 찾을 때까지 가로 방향으로 진행되며, 깊이가 아니라 거리 순에 따라 진행된다.

BFS 사진출처

BFS 탐색의 진행

1. 각 반복 때마다 상태 S의 모든 자식 노드를 생성하고, 이들은 open list 에 추가한다.
   =이때 list의 마지막에 추가한다(FIFO(First in-Fist out) 데이터 구조로 유지)
   =가장 마지막에 open list에 들어간 상태가 먼저 나가게 된다.
2. open list와 closed list는 결국 list이므로 순서가 정해져있다. (알파벳 순서대로 임의로 작성 X)

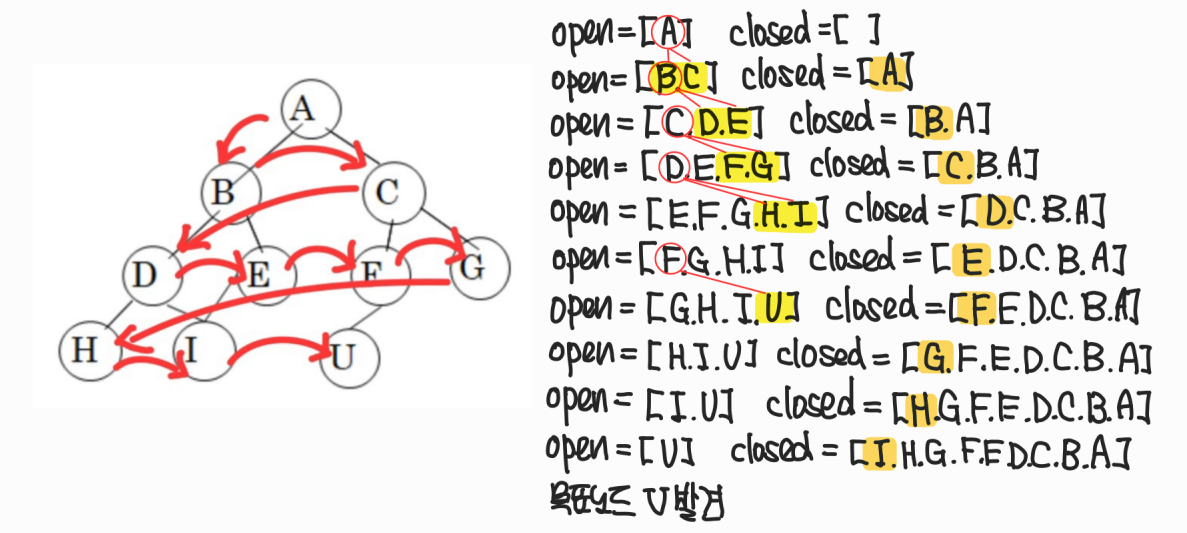
BFS 탐색시 open list와 closed list

BFS는 FIFO 구조로 open list에서 자식 노드가 append()로 추가 된다.
open list의 순서를 작성할 때는 검사하는 상태가 뭔지를 확인하며, 그 자식 노드를 리스트의 뒤에서 왼쪽 순서대로 작성해야 한다.
(노란색 형광펜 참고)
closed list를 작성할 때는 검사된 것을 추가하고, 순서는 그 코드에서 append()를 쓰면 뒤로, insert(0,state)를 쓰면 앞으로 작성하면 된다.
(->open list의 순서는 중요하지만 closed list의 순서는 크게 상관없으므로 쓰여진 코드에 따라 작성)

BFS 전체 소스 코드 분석(8-puzzle)

BFS 성능의 분석

• 완결성(completeness) : 분기 계수 b가 유한하면, 반드시 해답 발견.

• 최적성(optimality) : 연산자 적용 횟수가 최소인 해답을 찾을 수 있음.

• 시간 복잡도(time complexity)와 공간 복잡도(space complexity) : 아주 간단한 문제가 아니라면 천문학적인 시간과 메모리 공간이 필요하며, 특히 시간 복잡도 보다 공간 복잡도가 더 문제임.

6. Deep-Limited Search (깊이 제한 탐색)

기본적인 것이 DFS와 같지만, 끝까지 깊이 들어가지 않고 한계를 정하여 더 이상 탐색하지 않고 백트래킹 하는 것이다.
깊이 제한 탐색 중 'IDDFS : Iterative Deepening DFS' 라는 것이 있다.

IDDFS의 장점

-DFS의 공간 효율성과 BFS의 완전성을 결합 (해답이 존재하는 경우, 가장 적은 비용을 갖는 경로)
-알고리즘의 응답성 : 초기 반복에서 작은 수의 노드를 사용하기 때문에 매우 빠르게 실행

---

맹목적인 탐색 방법 비교 DFS vs BFS

• DFS : 가장 깊이 갈 곳이 없을 경우 옆으로 탐색
  -사용하는 경우 : 미로 찾기 / 그래프의 위상 정렬 / 전체 탐색 / 연결 구성 요소 찾기
  -구현하는 방법 : Stack 또는 재귀함수를 사용하여 구현
• BFS : 인접한 노드를 먼저 탐색하는 방법
  -사용하는 경우 : 최단 경로 문제 / 두 정점 u,v간 최단 경로

DFS-BFS 사진출처

---

7. 언덕 등반 기법 : hill-climbing(DFS)

각 노드에 대한 평가 함수값을 계산하여, 좋은 노드를 먼저 처리하는 것이다.
평가함수로는 $h(n)$ 을 사용하며, 제 위치에 있지 않은 타일의 수이다.
자식 노드 중 평가함수의 값이 가장 좋은(값이 작을 수록 좋음) 자식 노드를 선택하여 처리한다.
(오로지 $h(n)$ 함수만 이용하며, open list, closed list를 사용하지 않음)

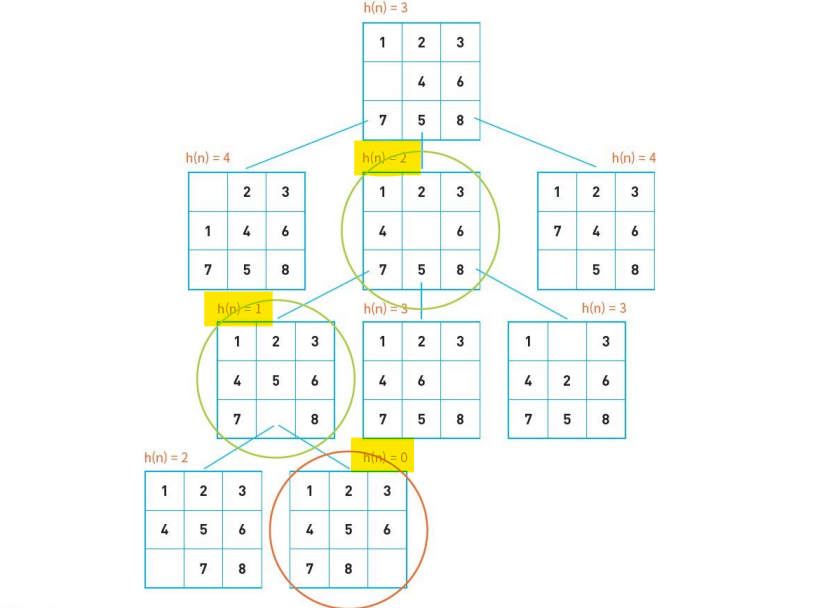
지역 최대 문제(local maximum problem) : 생성된 자식 노드의 평가 함수값이 부모 노드보다 안 좋을 경우 평가 함수값을 낮추는 방향으로 진행하는 것이 불가능하다.
=지역 최대값만 찾을 수 있을 뿐, 전역 최대값을 찾지 못 하는 경우가 발생함.

8. 최고 우선 탐색 : Best-First Search

언덕 등반 기법에서 개선한 것으로, 평가 함수와 open, closed list를 함께 사용한다.
open 리스트에서 처리할 노드를 선택할 때 가장 유망한 노드 순으로 선택한다.
그렇기에 평가 함수가 낮은 노드를 버리고 탐색을 안 하는 언덕 등반 기법과 달리
최고 우선 탐색은 선택 받지 못 한 노드들이 선택 될 가능성을 가지게 된다.

9. A* 알고리즘(BFS)

앞선 최고 우선 탐색에서는 오직 목표 노드와의 차이 h(n)을 고려하였지만, A* 알고리즘은 노드의 거리까지 추가하여 계산하다.
시작 노드에서 멀어지는 것은 결국 비용이 더 드는 것이므로 평가함수에 경로의 비용도 추가한 것이다.

$f(n)=g(n)+h(n)$

$g(n)$ : 시작 노드에서 현재 노드까지 오는 비용(시작 노드는 0부터 시작)
$h(n)$ : 현재 노드에서 목표 노드까지의 추정 거리(목표 노드와 제 위치에 맞지 않는 타일의 수)

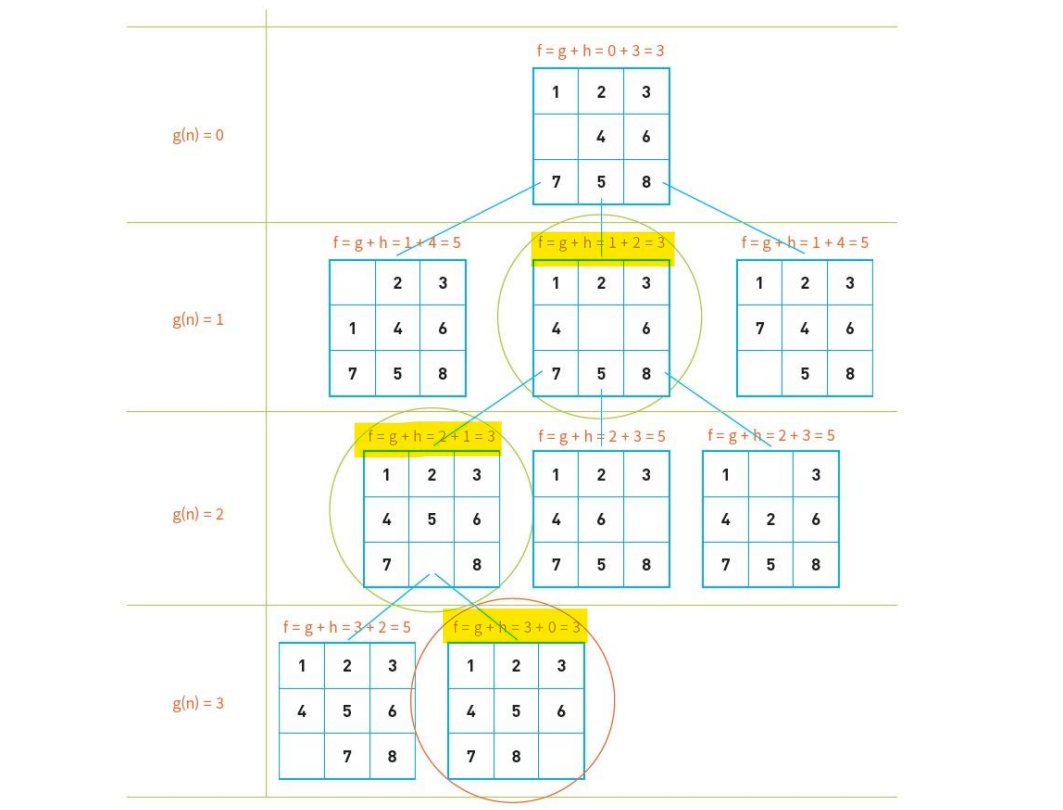
A* 알고리즘 전체 소스 코드 분석(8-puzzle)