classfication(분류) 문제
: 새로운 데이터가 입력되었을 때, 그 input data의 class를 찾는 것

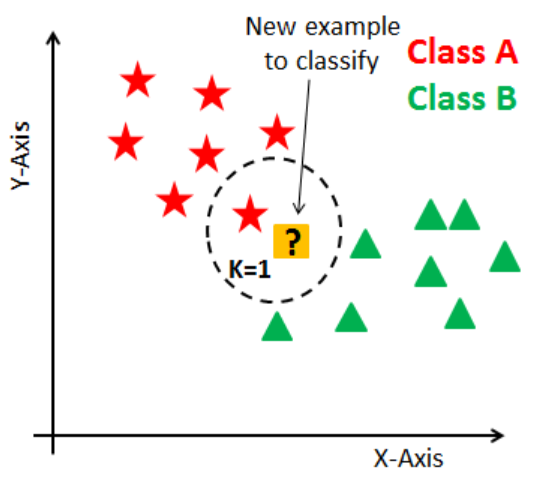
1. 최근접 이웃 (Nearest Neighbor)

최근접 이웃 알고리즘

Idea

새로운 입력 데이터를 기존에 있는 값들 중에서 가장 비슷한 것으로 분류
-> 수학적으로 가장 가까운 거리에 어떤 데이터가 있는지를 계산하여 분류
(일반적으로 사용하는 거리 측정 : Euclidean Distance)

Algorithm
$x$가 주어졌을 경우, 가장 가까운 거리에 있는 데이터
$x^*= argmax_x Distance(x, x_i)$
Output : $Class(x^*)$

사진 출처

2. Noisy Sample

: 최근접 이웃, $k=1$일 때의 문제점 ( $k$ : 이웃의 수)

서로 다른 class의 data라도 분포가 서로 섞일 수 있음

• 구분하기 어려운 sample 수집
• label 실수 (class에 label을 매기는 작업에서 실수할 수 있음)
• 특수한 사건

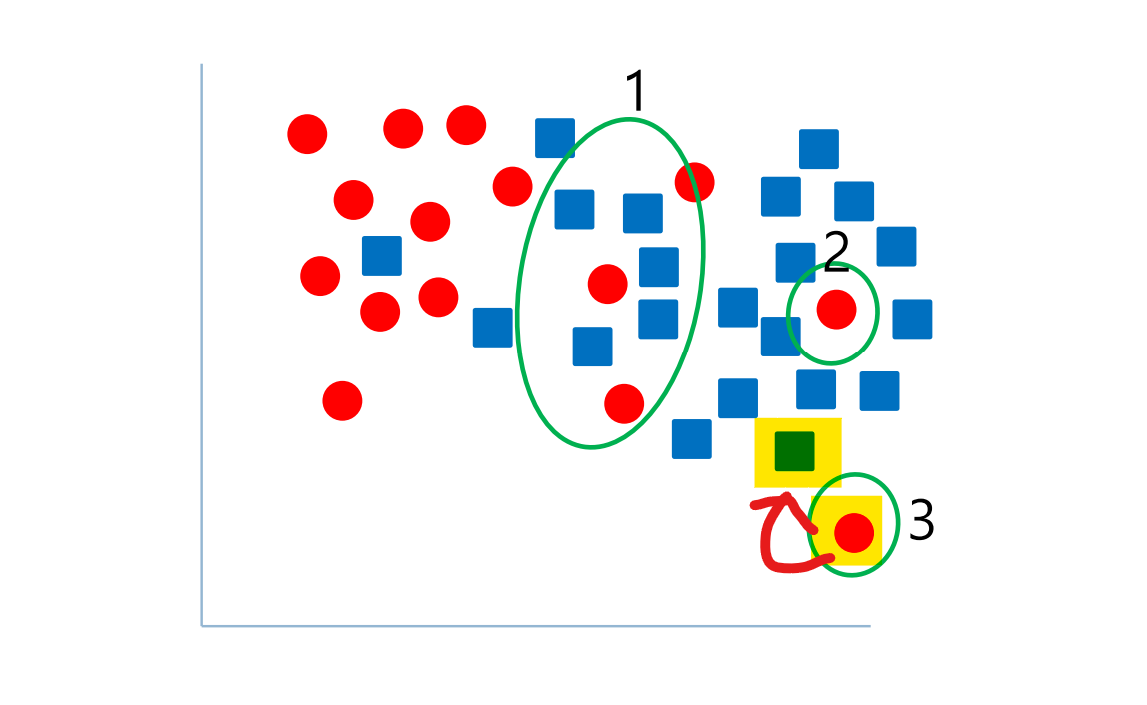
최근접 이웃 알고리즘은 Noisy sample로 인해 성능이 떨어질 수 있다.
위의 사진 예시처럼 3번의 경우, 가까운 빨간색 data의 영향을 받아 class를 잘못 분류하게 된다.

3. K-Nearest Neighbor (KNN)

Noisy sample로 발생할 문제를 해결할 수 있다 (비교할 이웃 $k$를 늘리는 방법)

• 데이터를 관측
• 거리를 계산 (다른 데이터들 간의 거리를 계산)
• 이웃을 찾기 (거리에 따라서 이웃 원들을 정렬)
• 새로운 데이터에 대하여 투표 (가장 가까운 k개의 이웃 중에서 가장 많은 표를 얻은 class로 분류)

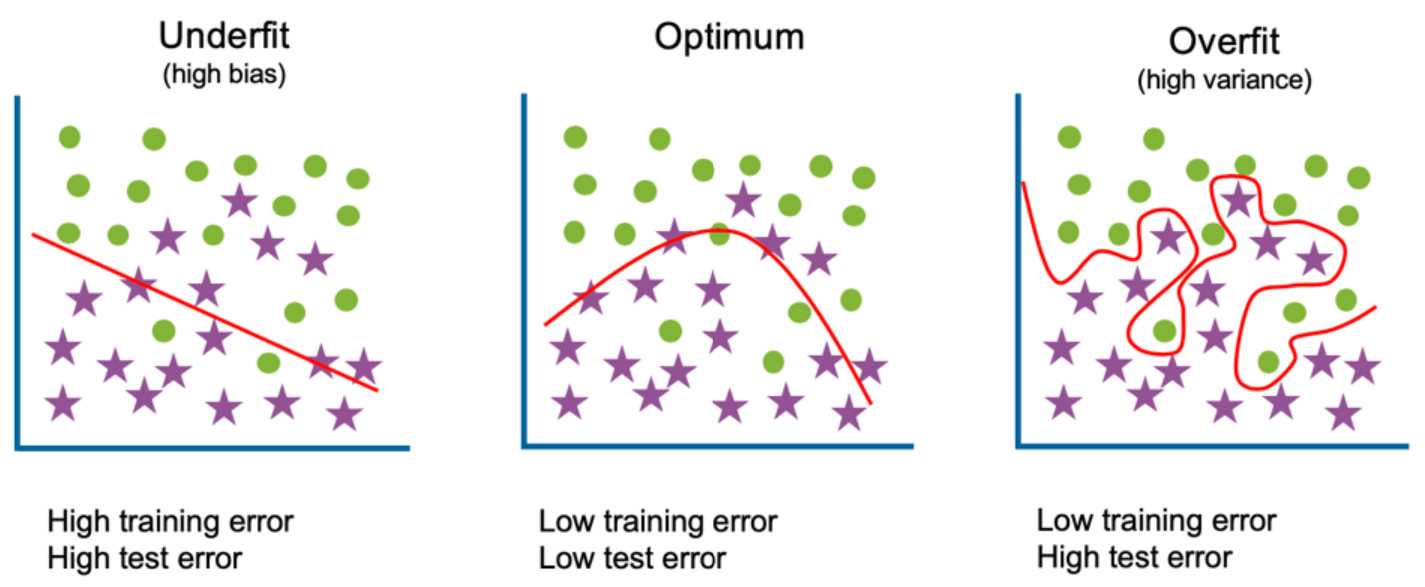
4. K Value와 Decision Boundary

KNN 알고리즘은 $k$값에 따라 성능이 변한다 -> 최적의 $k$를 찾는 것이 중요

• $k$가 너무 클 경우, Underfitting 발생
• $k$가 너무 작을 경우, Overfitting 발생

(Underfitting과 Overfitting은 머신러닝에서 나올 수 있는 안 좋은 성과이다.)

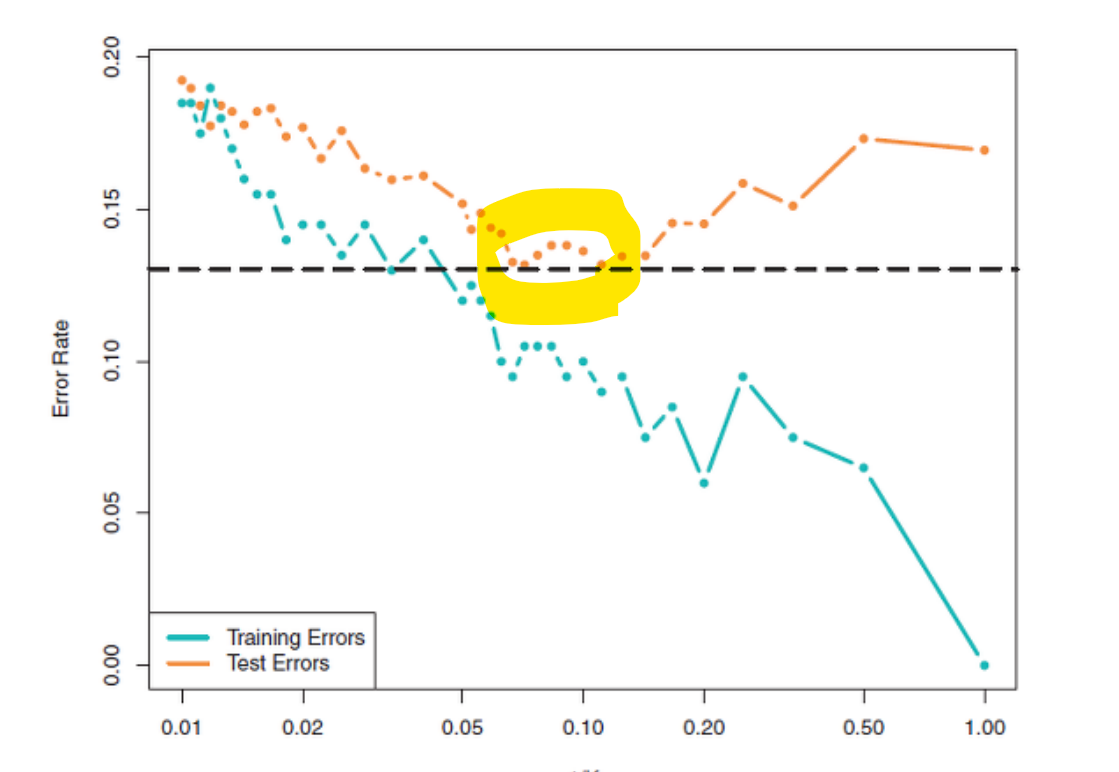
최적의 $k$ 값 찾는 방법

Training error와 Test error를 비교하며, 특히 Test error가 가장 낮아지는 $k$ 지점을 확인하며 찾는다

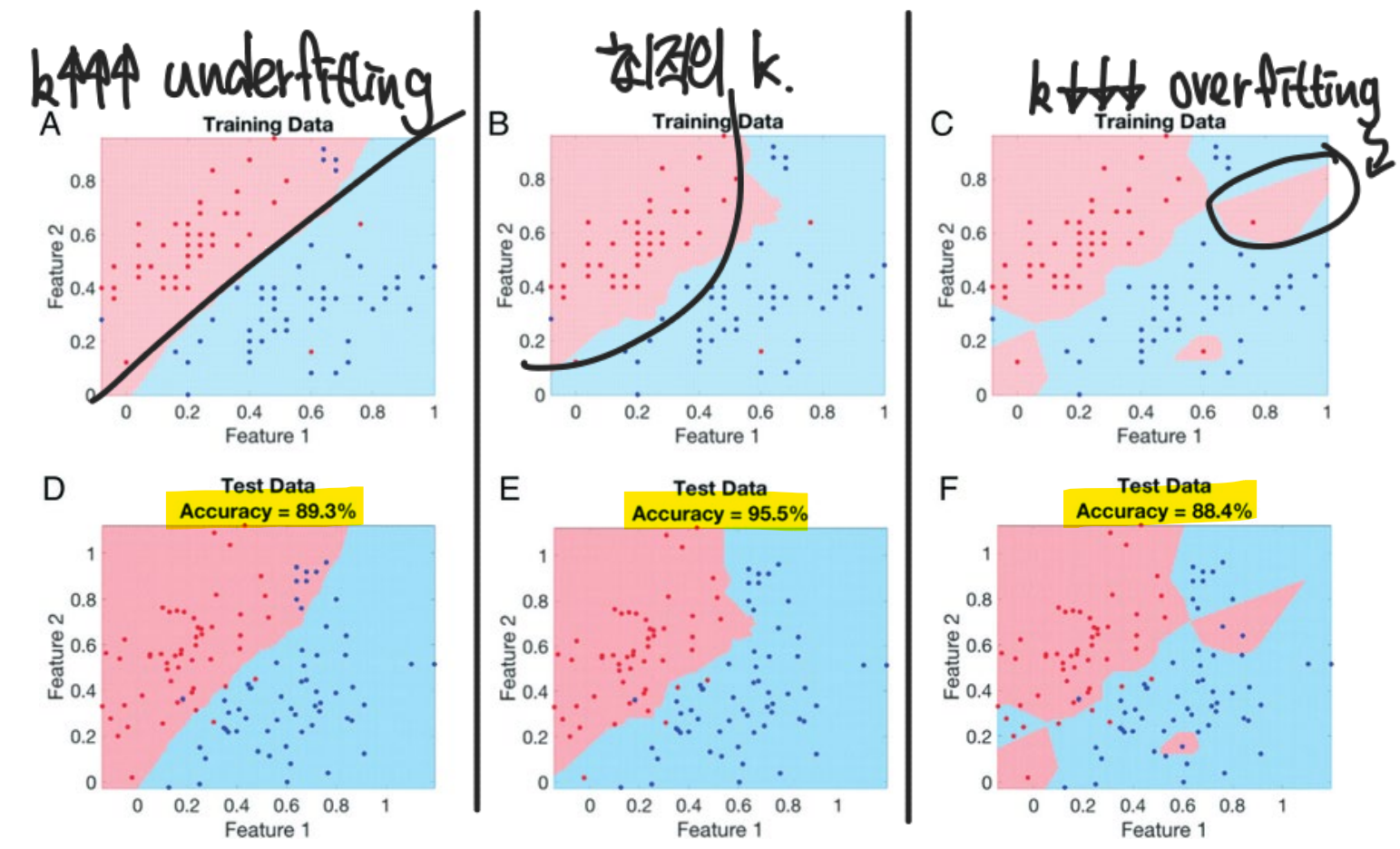
5. KNN 알고리즘 장단점

장점

• 단순하고 효율적이며, 훈련 단계가 빠르다
• 수치 기반 데이터 분류 작업에서 성능이 우수하다

단점

• 모델을 생성하지 않아 feature과 class 간 관계를 이해하는데 제한적이다
• 최적의 $k$ 선택이 필요하다
• data 수가 많아지면 느려진다

6. KNN 실습

data, target 분리

from sklearn.datasets import load_iris

dataset=load_iris()

data=dataset.data
target=dataset.target

train set, test set 분리

from sklearn.model_selection import train_test_split

train_data, test_data, train_target, test_target=train_test_split(data, target, test_size=0.2, random_state=42)

print(train_data.shape)
print(test_data.shape)

KNN 모델 학습

from sklearn.neighbors import KNeighborsClassifier

model=KNeighborsClassifier()
model.fit(train_data, train_target)

print(model.predict(test_data))
print(model.score(test_data, test_target))

---

추가 공부

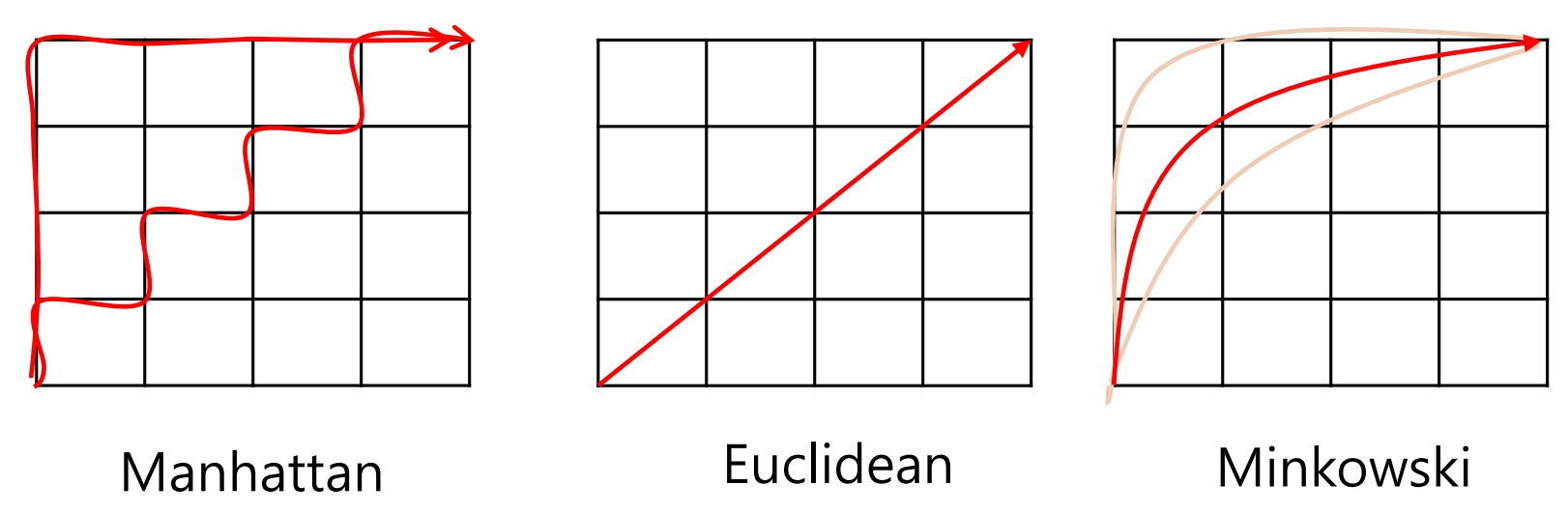
거리 측정 방법 (Distance Metrics)

: Manhattan Distance / Euclidean distance / Minkowski distance

Manhattan Distance $𝑑_𝑀 = |𝑥_2 − 𝑥_1| + |𝑦_2 − 𝑦_1|$

좌표의 절대 차이의 합

Euclidean distance $𝑑_𝐸 = \sqrt{(𝑥_2 − 𝑥_1)^2 + (𝑦_2 − 𝑦_1)^2}$

두 점 사이의 직선 거리 (최단거리)
(일반적으로 사용되는 거리 측정 방법이다)

Minkowski distance $𝑑_M =$ $^p\sqrt{(𝑥_2 − 𝑥_1)^p + (𝑦_2 − 𝑦_1)^p}$ $𝑝 ∈ (1.0,2.0)$

Manhatten 과 Euclidean 의 중간
(특수한 조건이 있을 때 사용, 장애물이 있는 경우 $p$ 값을 조절해 피할 수 있다)

마크다운 수식 참고

데이터 정규화 (Data Normalization)

Data feature의 단위 혹은 스케일이 다를 때, Distance는 단위가 큰 feature에 더 큰 영향을 받는다
그래서 서로 다른 feature들의 크기를 통일하기 위해 정규화를 사용한다

Min-Max Normalization $x_k=\frac{x_k - min(x)}{max(x) - min(x)}$

모든 feature가 0과 1 사이에 위치하도록 변경하는 방법

Z-Score Normalization $x_k=\frac{x_k - mean(x)}{std(x)}$

모든 feature에 대하여 평균이 0, 분산이 1인 값으로 변환하는 방법

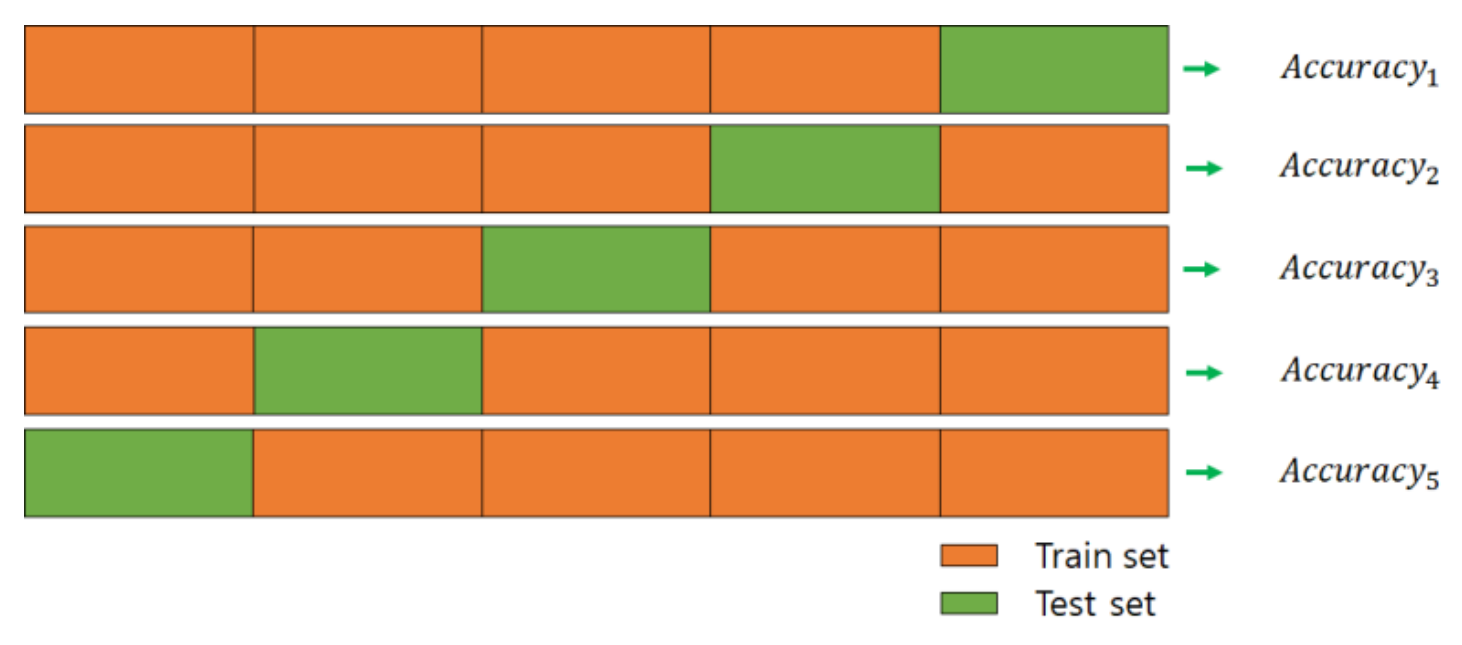
교차 검증 (Cross Validation)

test dataset에 따라 모델의 평가가 달라질 수도 있기에, test dataset이 편향되면 결과가 부정확할 수도 있다
이를 해결하고자 교차 검증을 사용한다

K-Fold cross validation

데이터를 K개의 subset으로 나누고, K번 테스트를 진행
그리고 K번 진행한 test set의 error를 평균내서 모델의 성능을 검증
(주로 5-Fold cross validation을 사용한다)

장점 : 데이터 편향 막을 수 있음/모든 데이터셋 평가/적은 수의 데이터라도 여러 번 평가/데이터 수 부족으로 인한 underfitting 방지
단점 : 모델 훈련 및 평가 시 시간이 오래 걸림