기존의 시퀀스 변환 모델 (seq to vector / seq to seq)에는 RNN과 CNN이 주로 사용되었다. 그러나 이들은 길이가 긴 시퀀스를 처리하게 될 경우 현저한 성능 저하를 보인다는 한계점이 점차 대두되었다. 이로 인해 NLP 분야의 성능 향상이 정체될 무렵, 2017년에 출간된 이 논문은 AI 기술 전반에 혁신적인 변화를 불러 일으켰다.

Introduction

RNN, LSTM, gated RNN, encoder-decoder 아키텍쳐

RNN -> 입력 및 출력 시퀀스의 심볼 위치(t)를 따라 계산 수행
h(t-1), t를 인풋으로 하고, 이를 통해 ht 산출 -> 심볼 위치가 선형적으로 이동하면서 분석을 수행하기에 병렬화 X ==> 인수분해 및 조건부 계산 등으로 모델 성능을 향상시킨다 해도 근본적인 문제는 남아 있음

attention 매커니즘은 시퀀스의 길이에 관계 없이 종속성을 모델링할 수 있도록 해줌 (필요한 것만 골라서 쓰니까)

attention만 전적으로 활용하는 transformer 개발 ==> 더 많은 병렬화와 더 빠른 학습

Background

기존의 모델은 시퀀스 거리에 따라 연산 횟수가 증가하게 된다.

ConvS2S -> 선형적
ByteNet -> 대수적

이로 인해 멀리 떨어진 것들 간의 종속성을 학습하기 어려워진다는 문제가 발생한다.

트랜스포머는 attention scores를 가중치로 삼아 각 위치의 value들에 곱함으로써 선형적인 학습 방식이 아닌, 병렬화된 학습을 수행할 수 있음 --> 이 과정에서 연산 과정을 줄어들어 속도가 향상되지만 가중평균화로 인해 일부 데이터가 소실되는 문제점이 발생할 수 있음 -> 그러나 이 마저도 multi-head attention을 통해 선형결합을 시켜주면 해결 가능

self-attention, end-to-end memory network는 attention 매커니즘을 활용하여 다양한 nlp 과제에서 우수한 성능을 냄.

그러나 트랜스포머는 전적으로 attention에만 의존하는 최초의 모델!

Model Architecture

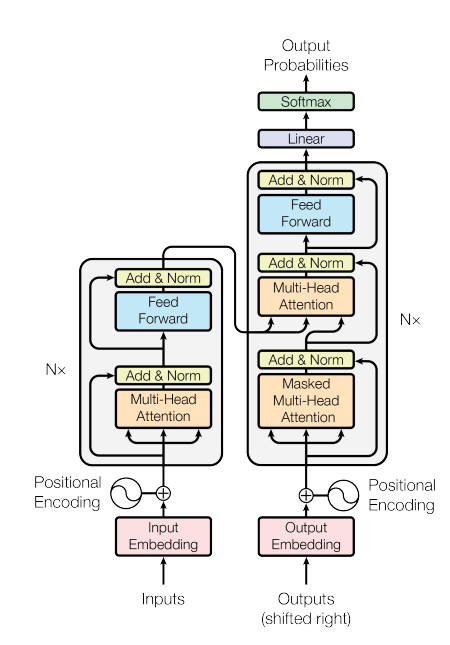
• encoder와 decoder로 구성되어 있고, encoder과 decoder는 각각 동일한 6개의 layer stacks로 구성되어 있음.

Encoder and Decoder Stacks

Encoder

각 layer는 2개의 sublayer로 구성되며, 각각의 sublayer에서 도출된 결과는 Add & Norm과 연결되어 residual connection, layer normalization 과정을 거치게 된다.

residual connection: 네트워크 깊이가 증가할 때 발생하는 gradient 소실(vanishing) 및 폭발(exploding) 문제를 해결하기 위해 사용하는 방법으로, sublayer의 출력값(Sublayer(x))에 입력값(x)을 더해 본래의 gradient 값을 유지함으로써 학습의 안정성을 제고하는 방식이다.

layer normalization: 각 층이 일정한 평균과 분산을 갖도록 정규화하여 학습 안정화, 속도 향상, 특성 중요도의 일관된 반영 등을 달성한다.

encoder의 sublayer들은 Multi-Head Attention과 Feed Forward로 이루어져 있는데, 이는 뒤에서 일괄적으로 설명할 예정이다. 또한 모델 layer들의 전반적인 작업이 원활히 수행될 수 있도록 output의 차원값을 512로 설정하였다.

Decoder

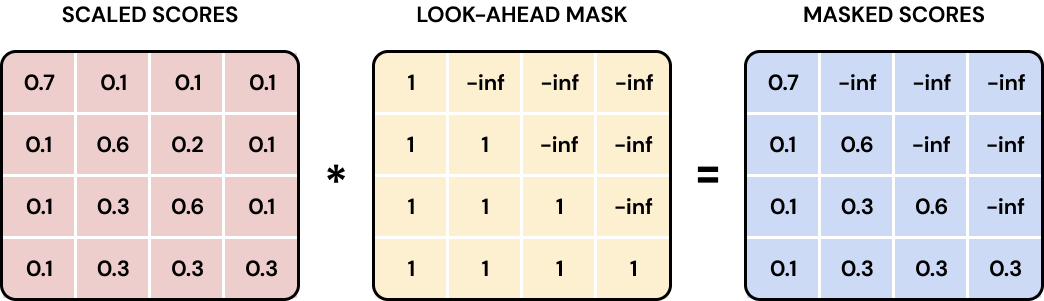
encoder의 구성과 거의 비슷하나, 한 가지 다른 점은 Masked Multi-Head Attention이 추가되었다는 점이다. decoder의 경우, 실제로 다음 단어에 대한 예측값을 도출해야 하기 때문에 attention layer에 masking 작업을 해준다. 이를 통해 디코더가 현재 위치 이후의 정보에 대해 접근하지 못하도록 하여 다음 토큰에 대한 예측을 효과적으로 수행할 수 있다.

Attention

Attention 매커니즘의 핵심 포인트는 query와 key-value 쌍을 매칭시키는 것이며, 매커니즘의 output은 value들의 weighted sum이 된다.

query와 key의 유사도를 계산하여 해당 key와 매칭된 value의 가중치를 구한다. 그리고 이를 통해 value들의 weighted sum을 도출한다.

Scaled Dot-Product Attention

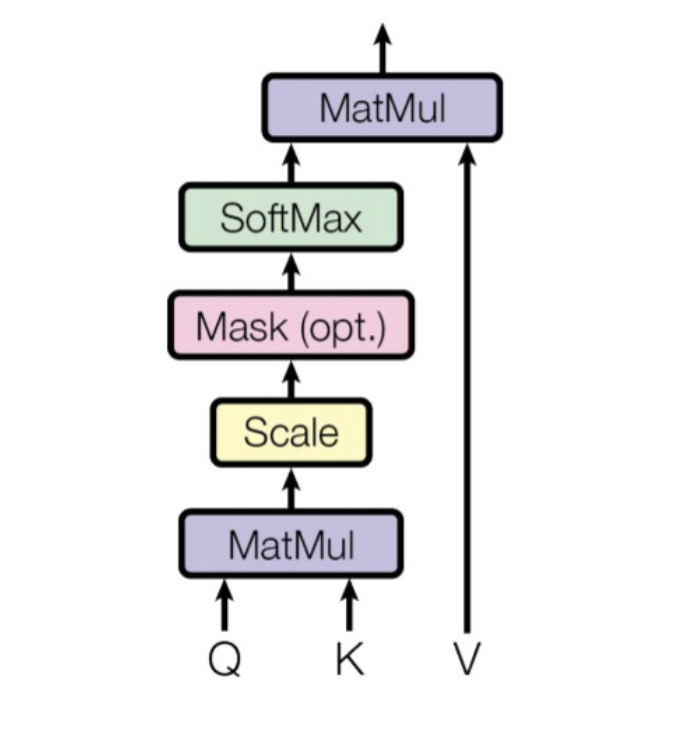
우선 임베딩된 문장 행렬에 Query, Key, Value에 해당하는 가중치 행렬을 곱하여 3개의 서로 다른 행렬 (Q, K, V)들을 생성한다. 이후 Q와 전치된 K를 서로 내적(dot-product)한다.

내적은 두 벡터의 유사도를 계산하기 위한 방식으로, 값이 클 수록 코사인 유사도에 의해 유사도가 높아지게 된다.

내적값이 지나치게 커지게 될 경우, softmax 함수의 gradient가 0에 수렴하게 되므로 이를 방지하기 위해 key의 차원값으로 scaling을 해준다. 그리고 도출된 결과를 softmax 함수에 통과시켜 각 값의 총합이 1이 되는 가중치 행렬로 변환시킨다. 이를 Value 행렬과 곱해주면 최종적으로 구하고자 하는 Attention Score (weighted sum) 값이 나오게 된다.

위 과정을 식으로 표현하면 다음과 같다.

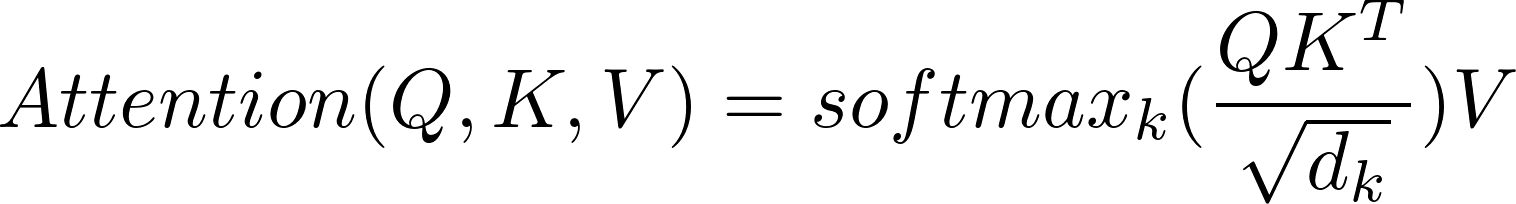
이 논문에서는 기존의 additive attention이나 dot-product attention이 아닌 scaled dot-product attention을 사용하였는데, 이는 일반적으로 성능이 더 뛰어난 dot-product attention의 장점을 차용하면서도 scaling을 통해 gradient 소실 문제를 해결하기 위해서이다.

Multi-Head Attention

모델 전체 차원에 대해 일괄적으로 single attention 매커니즘을 적용할 경우, 문제가 발생한다. head가 하나이기 때문에 입력 데이터를 구성하는 subspace의 모든 정보를 한번에 처리하기 위해서는 평균화 과정이 필수불가결하게 요구된다. 때문에 subspace의 정보가 일부 소실될 수밖에 없고, 정확도 저하 문제가 발생하게 된다.

이를 해결하기 위해 Multi-Head Attention이라는 개념이 등장하였다.

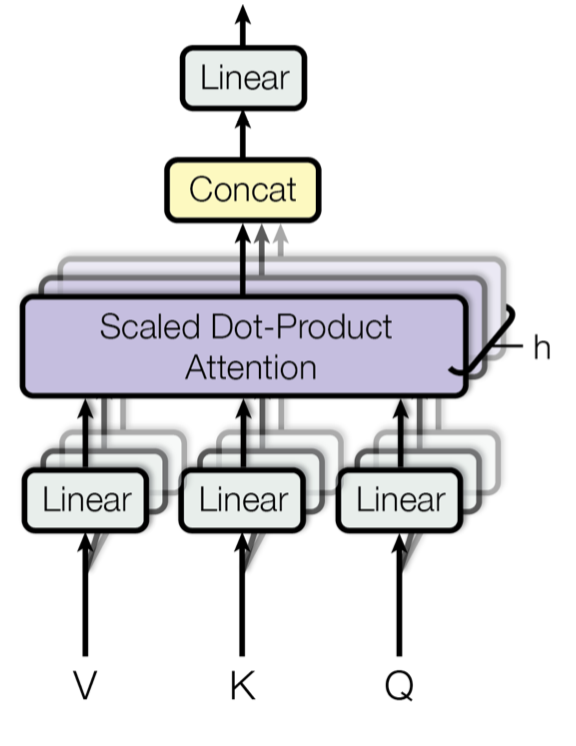
간단하게 말하면, head를 여러 개로 나눠서 병렬로 처리한 다음에 하나의 attention score로 합치는 방식이다.

구체적으로 head는 총 h개의 subhead로 나누어진다. 논문에서와 같이 num_heads가 8이고 입력값의 임베딩 차원이 512일 경우, 각 subhead의 차원은 64가 된다. 입력값으로 받은 Query, Key, Value에 각 head에 해당하는 가중치 행렬들을 곱하면 해당 head의 Q, K, V 행렬이 도출되는데, 이를 입력값으로 삼아 각각의 head에서 attention 매커니즘을 수행한다.

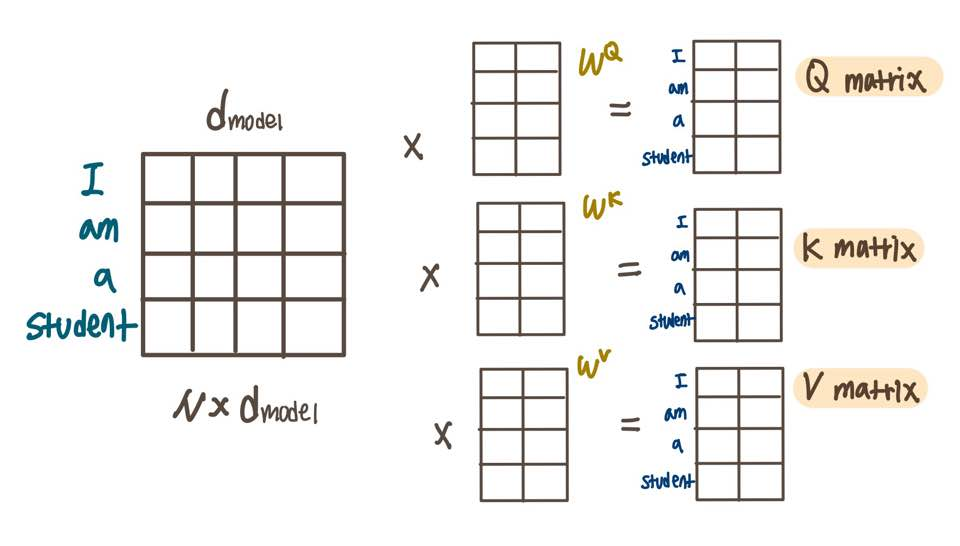
출처: https://velog.io/@aqaqsubin/Transformer-Attention-Is-All-You-Need

이후 병렬 연산을 마치고 나면 각 head에서 계산된 weighted sum을 하나로 연결 (concatenate)하고, 최종 가중치 행렬을 곱하여 합친 값들을 고르게 scaling해준다. 이렇게 해서 산출된 attention score의 값이 Multi-Head Attention의 출력값이다.

기실, Multi-Head Attention의 결과값은 Single Attention과 다르지 않다. 다만 Multi-Head Attention은 다음과 같은 측면에서 분명한 우위를 지닌다.

다양한 관점에서의 정보 수집: 각 head가 입력에 대해 서로 다른 관점에서 정보를 추출하도록 한다. 즉, 매커니즘이 각각의 subspace에 대해 공동으로 attend함으로써 다양한 특징과 패턴을 학습할 수 있는 것이다.

표현 능력 강화: 각 head는 독립적으로 학습되므로 모델은 여러 가지 표현을 동시에 학습할 수 있다. 이는 모델이 높은 수준의 추상적인 정보를 학습하고 복잡한 관계를 모델링하는 데 도움이 된다.

과적합 감소: Multi-head attention은 각 head가 독립적으로 작업을 수행하므로, 하나의 head에서 과적합 현상이 발생해도 다른 head들이 이를 보완할 수 있다.

병렬화 가능: Multi-head attention은 각 head가 독립적으로 계산되기 때문에 병렬 연산이 가능하며, 이는 모델의 훈련 속도 향상으로 귀결될 수 있다.

Applications of Attention in our Model

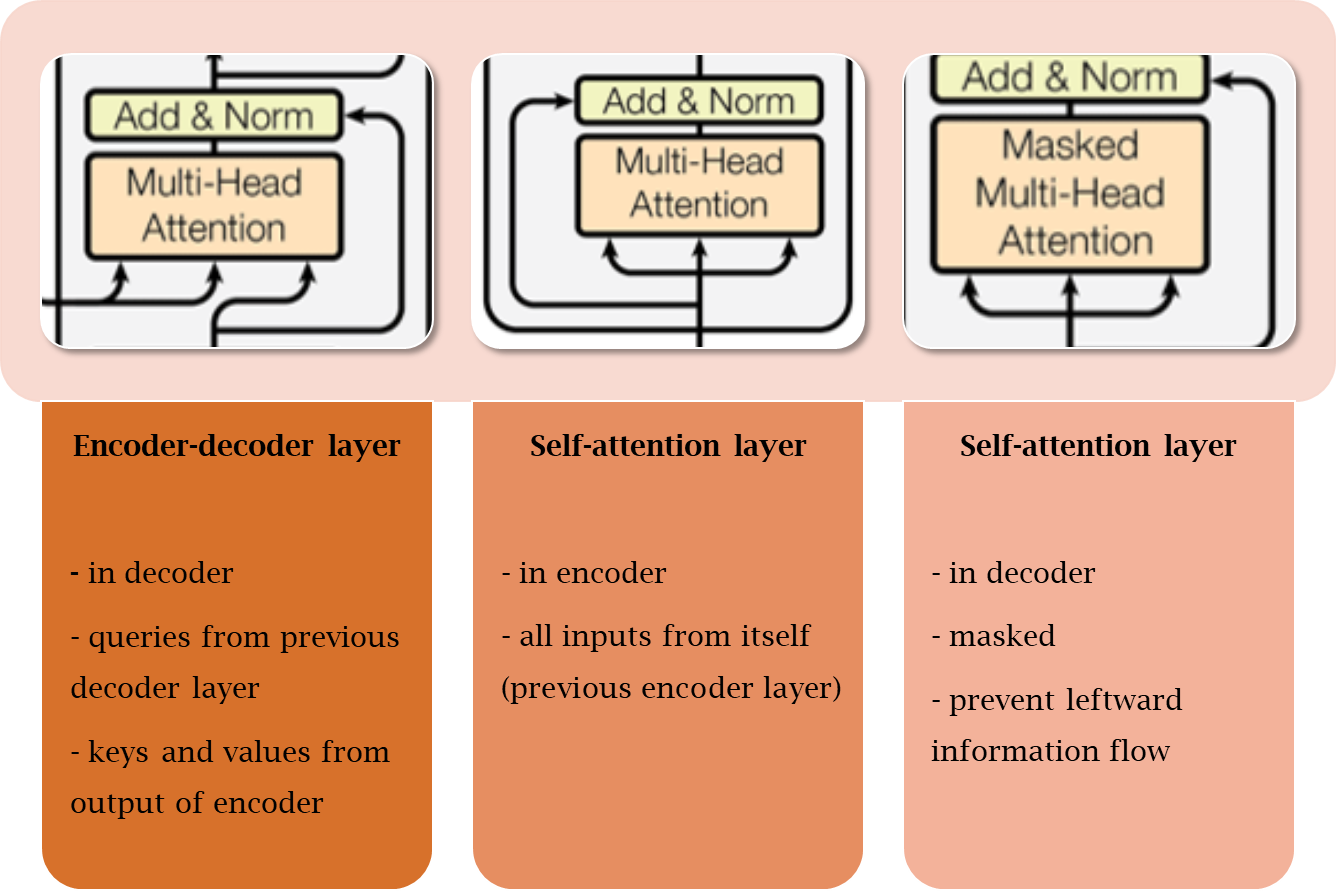
Position-wise Feed-Forward Networks

encoder와 decoder에는 공통적으로 fully connected feed-forward network가 존재한다. 이는 두 개의 linear transformation과 ReLU 활성화 함수로 구성되어 있는데, 구체적인 식은 다음과 같다.

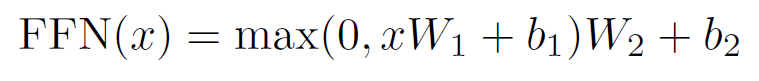
FFN은 두 개의 은닉층으로 이루어진 신경망이라 보아도 무방하다. 2048의 차원을 갖는 가중치 행렬 W1을 통해 선형 변환을 수행하고, 이를 ReLU 활성화 함수에 대입한다. 그리고 활성화 함수의 결과값을 한번 더 선형 변환해줌으로써 최종 결과값을 도출한다.

이 같은 과정을 거치는 이유는 position-wise, 즉 토큰의 위치와 관련하여 해당 위치에서의 중요한 특징을 추출하기 위해서이다. 또한 ReLU 함수를 사용하면 모델에 비선형성을 추가되는데, 이는 모델이 단순히 선형적인 관계만이 아닌, 조금 더 복잡한 연관성을 학습할 수 있도록 돕는 역할을 한다.

Embeddings and Softmax

여타 시퀀스 변환 모델과 마찬가지로 transformer에서도 학습된 임베딩을 사용하여 입력 토큰과 출력 토큰을 512 차원의 임베딩 벡터로 바꾸는 과정을 수행한다. 또한 decoder의 마지막에 softmax 함수를 배치하여 출력값을 다음 토큰 후보에 대한 확률분포로 변환하는 과정 역시 수행한다.

Positional Encoding

Transformer에는 recurrence와 convolution이 없기 때문에 토큰의 선후 관계나 거리에 대한 정보를 활용하기 어렵다. (문장의 뜻이 아예 달라지는 문제 발생) 모델이 이러한 시퀀스의 순서 정보를 활용하려면 분석 이전에 토큰의 위치 정보를 주입해야 한다. 이를 위해 필요한 과정이 바로 positional encoding이다. 본 논문에서는 다음과 같은 수식을 통해 positoinal encoding을 수행하고 있다.

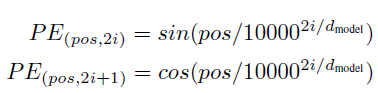
positional encoding에서 sine함수와 cosine함수를 사용한 이유는 바로 주기성 때문이다. 위치 벡터를 시퀀스 길이에 비례하여 정수형으로 부과할 경우, 거리가 길어지게 되면 단어 본연의 의미보다 위치값이 더 중요해지고 일반화가 불가능해진다는 문제가 발생한다. 하지만 그렇다고 정규화를 하면 위치 벡터의 상대성이 훼손되는 문제가 생긴다.

이 같은 문제점을 해결할 수 있는 방안은 바로 주기성을 띈 sine함수와 cosine함수를 사용하는 것이다.

의미 정보가 변질되지 않도록 위치 벡터값이 너무 크면 안된다. --> sine함수와 cosine 함수는 -1부터 1까지의 범위 내에서 출력값이 결정된다.

동일하게 범위가 정해진 sigmoid 함수와 달리 주기성이 있기 때문에 시퀀스의 길이가 극단적으로 길어지더라도 위치 벡터의 차가 미미해지지 않는다.

이를 활용하여 단어 벡터마다 함수의 frequency, sine/cosine 여부 등을 적절히 변경해가며 positional encoding을 해줄 경우, 효과적으로 위치 정보를 주입할 수 있게 된다.

참고: https://www.blossominkyung.com/deeplearning/transfomer-positional-encoding

Why Self-Attention

1. 계산 복잡도 감소 - 시퀀스 길이가 극단적으로 길어지면 self attention을 restrict함으로써 복잡도를 크게 감소시킬 수 있다.

2. 병렬화 - 병렬화를 통해 연산을 더욱 빠르게 수행할 수 있다.

3. 장거리 종속성 학습 - 시퀀스 변환 모델의 고질적인 문제점이었던 경로 길이 증가에 따른 학습에서의 비효율성을 해결할 수 있다.

4. convolution은 계산 비용을 높이는 대신 복잡도를 낮추었다. 그러나 이 낮춘 복잡도마저도 self attention의 복잡도와 거의 동일하다.

5. 해석 가능한 모델 제공 - 서로 다른 특징과 작업에 대한 학습의 정확도를 눈에 띄게 향상시킬 수 있다.

Conclusion

Transformer는 encoder-decoder 아키텍처에서 흔히 사용되는 recurrent layer를 전면 attention 매커니즘으로 대체하여 만든 모델이다.

비교적 단순한 원리로 구성되어 있지만, WMT 2014 translation task에 대해 모두 기존 앙상블 기반 모델보다 향상된 성능을 보이며 SOTA 모델의 자리를 차지하는 기염을 토했다.

Transformer는 현재 단순히 NLP에만 쓰이지 않고, 이미지/오디오/비디오와 같은 다양한 분야에도 적용되어 점차 활용 범위를 넓히고 있다.

Transformer의 미래는 무궁무진하고, 현재 AI 산업에서 가장 핫한 토픽이라고 볼 수 있다. Transformer에 대해 딥하게 공부하는 과정을 거쳐야 현재 트렌드에 대해서 제대로 이해할 수 있을 거라고 생각한다.