[컴퓨터그래픽스] Affine Transformations (아핀 변환)

Serun1017·2024년 10월 23일
컴퓨터그래픽스
0

컴퓨터그래픽스

목록 보기
24/31

Affine Transformations (아핀 변환)

Affine Transformations 은 선형 변환과 이동 변환이 결합된 변환이다. 직선을 직선으로 유지하지만, 평행선이 보장되지 않을 수 있다. 선형 변환에 비해 더 일반적인 변환이며, 그래픽스에서 많이 사용된다.

  • 3차원에 대한 아핀 변환은 4x4 행렬로 표현된다.
    [a11a12a13txa21a22a23tya31a32a33tz0001]\begin{bmatrix} a_{11} & a_{12} & a_{13} & t_x \\ a_{21} & a_{22} & a_{23} & t_y \\ a_{31} & a_{32} & a_{33} & t_z \\ 0 & 0 & 0 & 1\end{bmatrix}
  • 여기서 aija_{ij}는 선형 변환을 담당하고, tx,ty,tzt_x, t_y, t_z는 이동 변환이다.

Properties of Affine Transformations

Affine Transformations (아핀 변환) 은 Linear Transformations (선형 변환) 과 Translations (평행 이동)의 조합으로 이루어진다.

  • 아핀 변환은 직선을 직선으로 변환한다. 즉, 아핀 변환을 적용하더라도 직선은 휘어지지 않고 그대로 직선으로 남는다.
  • 아핀 변환은 평행한 선을 여전히 평행하기 유지한다. 두 직선이 변환전에 평행했다면, 변환 후에도 여전히 평행 관계를 유지한다.
  • 아핀 변환은 한 직선 위의 거리 비율을 유지한다. 즉, 직선 위에 있는 두 점 간의 상대적인 거리는 변하지 않지만, 전체적인 거리는 변할 수 있다.
  • 아핀 변환은 절대적인 거리와 각도를 보존하지 않는다. 즉, 변환을 통해 도형의 크기나 두 직선 사이의 각도는 변할 수 있다. 회전하거나 크기를 확대/축소 하는 경우가 이에 해당한다.

Example of Affine Transformations

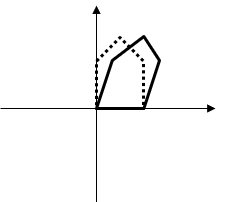
2D Rotation

(x′y′1)=(cos⁡θ−sin⁡θ0sin⁡θcos⁡θ0001)(xy1)\begin{pmatrix}x^\prime \\ y^\prime \\ 1 \end{pmatrix} = \begin{pmatrix} \cos{\theta} & -\sin{\theta} & 0 \\ \sin{\theta} & \cos{\theta} & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}

2D Rotation.png

2D Scaling

(x′y′1)=(sx000sy0001)(xy1)=(sxxsyy1)\begin{pmatrix} x^\prime \\ y^\prime \\ 1 \end{pmatrix} = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} s_x x \\ s_y y \\ 1\end{pmatrix}

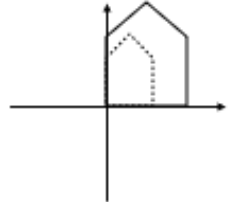
2D Scaling.png

2D Shear

(x′y′1)=(1d0010001)(xy1)=(x+dyy1)\begin{pmatrix} x^\prime \\ y^\prime \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & d & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1\end{pmatrix} = \begin{pmatrix} x+dy \\ y \\ 1 \end{pmatrix}

2D Shear.png

2D Reflection

(x′y′1)=(1000−10001)(xy1)=(x−y1)\begin{pmatrix} x^\prime \\ y^\prime \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1\end{pmatrix} = \begin{pmatrix} x \\ -y \\ 1 \end{pmatrix}

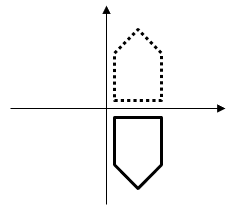
2D Reflection.png

2D Translation

(x′y′1)=(10tx01ty001)(xy1)=(x+txy+ty1)\begin{pmatrix} x^\prime \\ y^\prime \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1\end{pmatrix} = \begin{pmatrix} x+t_x \\ y+t_y \\ 1 \end{pmatrix}

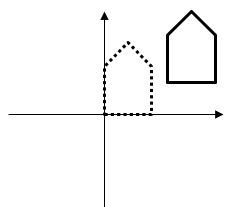
2D Translation.png

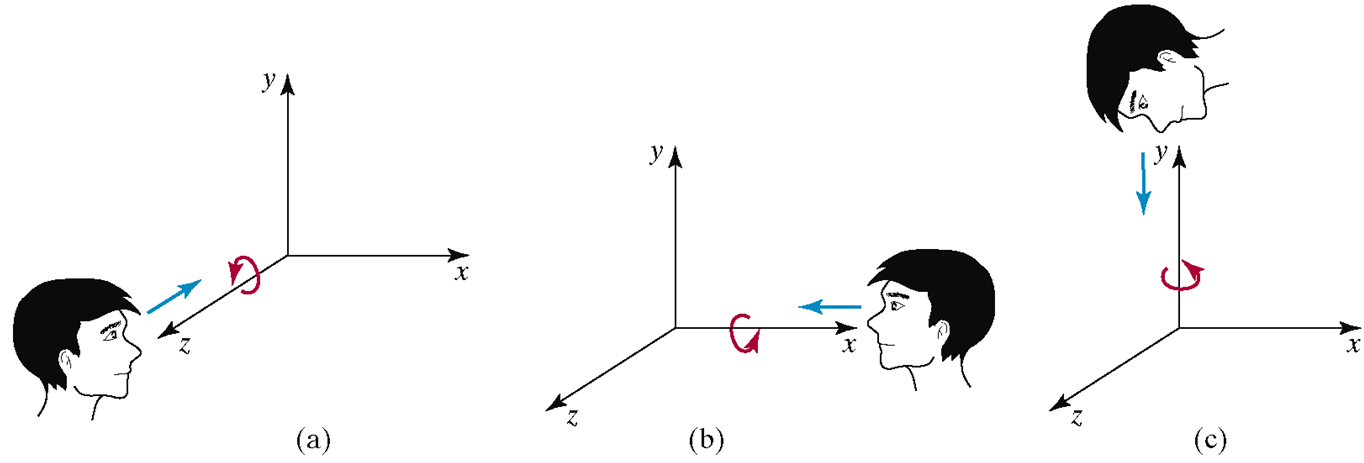
3D Rotation

x-rotation

(x′y′z′1)=(10000cos⁡θ−sin⁡θ00sin⁡θcos⁡θ00001)(xyz1)\begin{pmatrix} x^\prime \\ y^\prime \\ z^\prime \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos{\theta} & -\sin{\theta} & 0 \\ 0 & \sin{\theta} & \cos{\theta} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1\end{pmatrix}

y-rotation

(x′y′z′1)=(cos⁡θ0sin⁡θ00100−sin⁡θ0cos⁡θ00001)(xyz1)\begin{pmatrix} x^\prime \\ y^\prime \\ z^\prime \\ 1 \end{pmatrix} = \begin{pmatrix} \cos{\theta} & 0 & \sin{\theta} & 0 \\ 0 & 1 & 0 & 0 \\ -\sin{\theta} & 0 & \cos{\theta} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1\end{pmatrix}

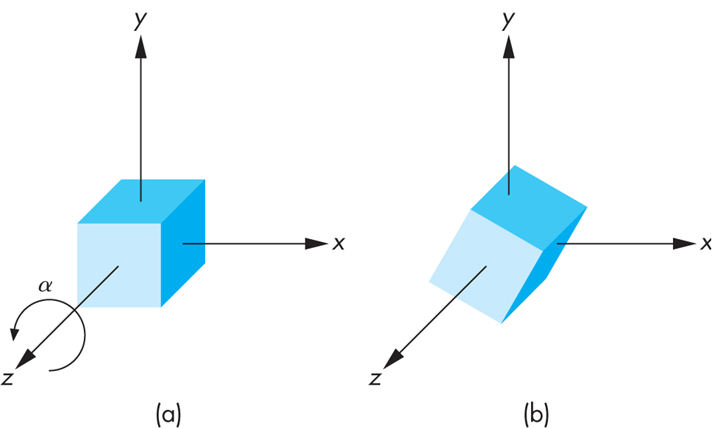
z-rotation

(x′y′z′1)=(cos⁡θ−sin⁡θ00sin⁡θcos⁡θ0000100001)(xyz1)\begin{pmatrix} x^\prime \\ y^\prime \\ z^\prime \\ 1 \end{pmatrix} = \begin{pmatrix} \cos{\theta} & -\sin{\theta} & 0 & 0 \\ \sin{\theta} & \cos{\theta} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1\end{pmatrix}

3D Rotation.png
3D Rotation_z-rotation.png

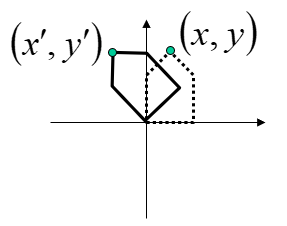
2D Pivot-Point Rotation

  • Rotation with respect to a pivot point (x,y)(x, y)
T(x,y)⋅R(θ)⋅T(−x,−y)=(10x01y001)⋅(cos⁡θ−sin⁡θ0sin⁡θcos⁡θ0001)⋅(10−x01−y001)=(cos⁡θ−sin⁡θx(1−cos⁡θ)+ysin⁡θsin⁡θcos⁡θy(1−cos⁡θ)−xsin⁡θ001)\begin{aligned} T(x, y) \cdot R(\theta) \cdot T(-x, -y) \\ &= \begin{pmatrix} 1 & 0 & x \\ 0 & 1 & y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} \cos{\theta} & -\sin{\theta} & 0 \\ \sin{\theta} & \cos{\theta} & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & -x \\ 0 & 1 & -y \\ 0 & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} \cos{\theta} & -\sin{\theta} & x(1-\cos{\theta}) + y\sin{\theta} \\ \sin{\theta} & \cos{\theta} & y(1-\cos{\theta})-x\sin{\theta} \\ 0 & 0 & 1 \end{pmatrix} \end{aligned}

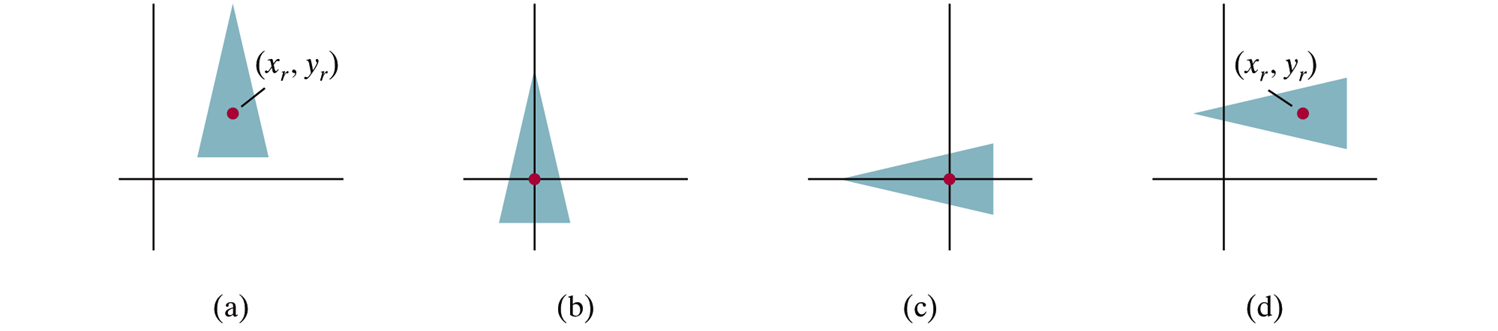
2D Pivot-Point Rotation.png

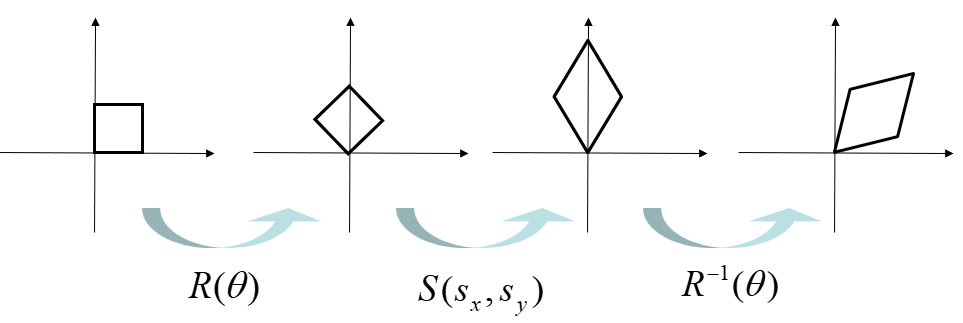
Scaling Direction

  • Scaling along an arbitrary axis
    R−1(θ)⋅S(sx,sy)⋅R(θ)R^{-1}(\theta) \cdot S(s_x, s_y) \cdot R(\theta)

Scaling Direction.png

profile
Serun1017
이전 포스트

[컴퓨터그래픽스] Rigid Transformations (강체 변환)

다음 포스트

[컴퓨터그래픽스] Projective Transformations (사영 변환)

0개의 댓글