---

Bayes Classifier

Bayes classifier의 경우 bayes rule을 활용해서 추론 가능한 확률분포를 만들어 문제를 해결하는 아이디어를 가지고 있습니다.

Why use Bayes's Rule???

주로 p(y|x)로 특정 입력 x가 주어진 경우 y 값이 나올 확률 예측합니다. 하지만 실제로 x들이 나올 확률은 알수 없습니다. 왜냐하면 실제 데이터들이 어떤 분포를 따르면서 샘플링 되었는지 알수 없기 때문입니다.
하지만 이를 베이즈 정리를 통해서 $p(y|x) = \frac{p(x|y)p(y)}{p(x)}$ 로 변형할수 있게 됩니다. 즉, y라는 라벨을 아는 경우 y에 대한 분포는 모델링이 가능합니다. 예를들어 이진 분류의 경우 y = {-1, 1} 값만 가지게 되기 떄문에 충분히 분포예측이 가능합니다.
단, 여기서 p(x) 값은 알수 없는데, 이는 주로 분모에 들어가 있어 생갸되는 경우가 대부분입니다. 그래서 베이즈 정리릍 통해서 복잡한 p(x)를 구하는 데신 P(x|y)로 우회해서 구하게 됩니다.

Risk 개념

Risk의 경우 Loss 의 기댓값으로 정의가 가능합니다. 그래서 classification의 최종 목표는 다음의 RISK를 최소화하는것입니다.

그래서 다음과 같이 표현할수 있습니다.

최종 RISK를 줄이는 행위는 , 결국 각 x에 대한 RISK를 최소하하는 것으로 직결되기 때문에 하나의 입력에 대한 조건부 확률로 표현함으로써 RISK를 최소하할수 있는식을 세울수 있습니다.

그리고 문제를 간단하게 보기 위해서 Binary Classification을 가정한다면

다음과 같이 나타낼 수 있습니다. 위의 식으로 전개가 된 이유는

다음 사진과 같이 y = 1과 y = -1 로 나눠서 RISK를 구하는 식에서 만일 y = 1일 확률이 y = -1 일 확률 보다 높다면 f(x) = 1이 되도록 설정하기 위함입니다.
$\mathrm{sign}\!\Bigl(\log\frac{P(Y=1\mid x)}{P(Y=-1\mid x)}\Bigr)$ 해당 식이 이를 만족하는 식이 되게 됩니다.

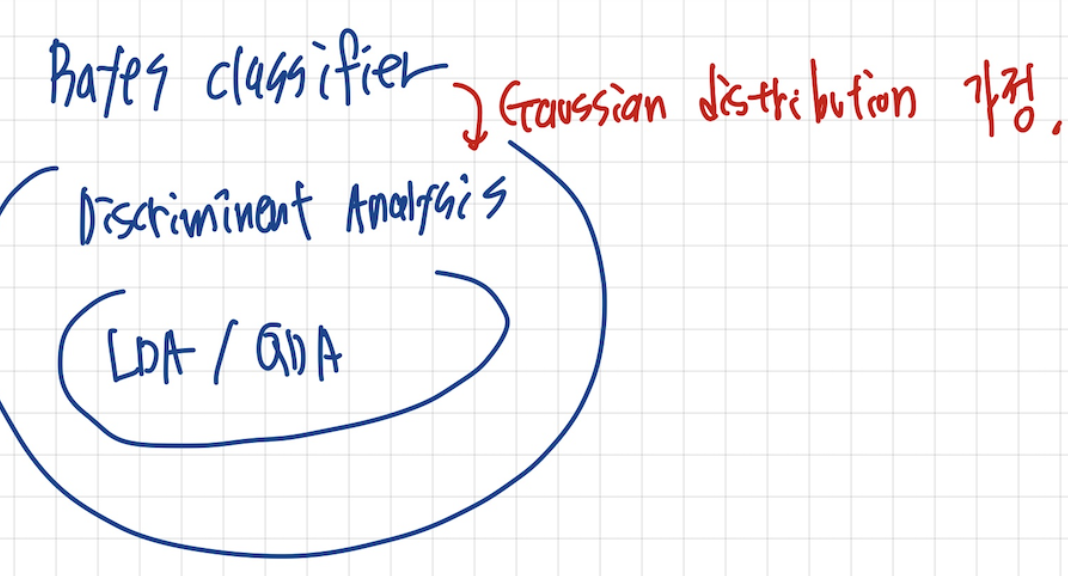
LDA & QDA

이제 위의식을 풀기위해서 p 함수를 알아야하는데, p는 우리가 알수 없습니다. 그래서 우리는 p함수가 Gauusian distribution을 따른다고 가정합니다.
이렇게 p(x|y)p(y)를 사용해서 분포를 추론하는것을 Generative Classifier라고 합니다.

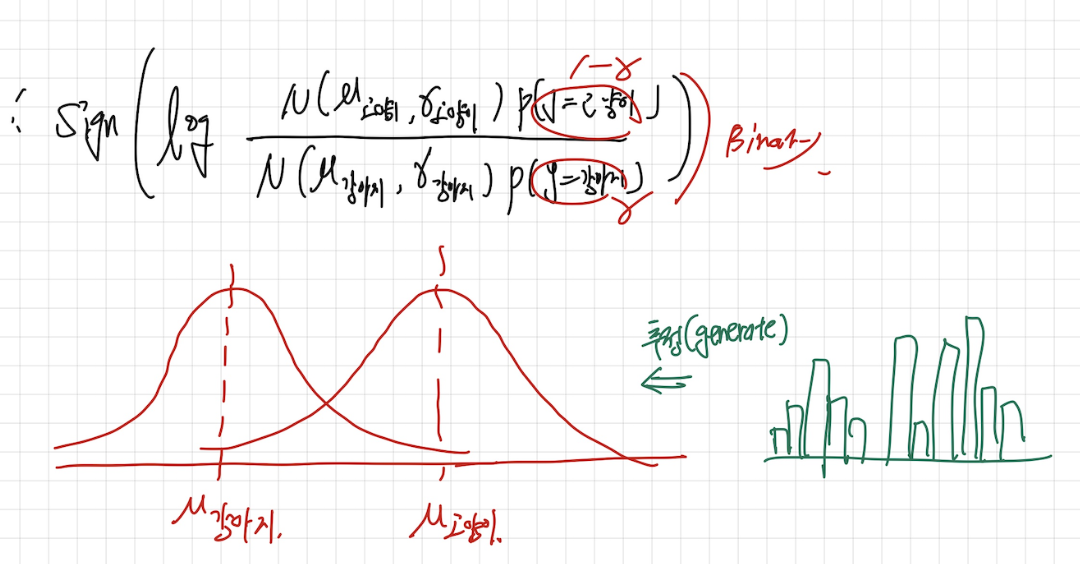
왜 Generative 인지는 위의 식을 통해서 알 수 있는데, 우리가 만일 고양이, 강아지를 구분하는 경우, 데이터들의 모수는 알수 없습니다. 하지만 고양이인 데이터들과 강아지인 데이터들의 데이터를 통해서 유추할수 있게 됩니다, 즉, 모수 분포와 비슷한 분포를 생성하게 되는 것입니다.

그리고 위의 식을 풀어서 $mu_{강아지}, \mu_{고양이}, \sigma(강아지), \sigma(고양이)$ 에 대해서 MLE를 풀어주게 되면 결국 각 클래스에 속하는 데이터들의 평균과 분산이 나오고 이를 QDA라고 합니다.

그리고 만일 $\sigma(강아지) == \sigma(고양이)$ 라는 가정을 두고 풀게되면 최종적인 식이 Linear 한 형태가 나오고 이를 LDA라고 부른다고 합니다.

Naive Classifier

Naive Classifier의 경우 Bayes classifier의 한 종류인데, p(x|y) 각 각각 독립적이라는 가정입니다. 이는 흔히 일어나는 가정은 아닙니다 예를들어 y = 강아지 에 대해서 이미지 x가 들어왔을때 , 각 픽세들은 독립이 아닙니다. 하지만 이를 사용하는 이유는 2개의 값을 비교할 수 있다는 장점이 있습니다.

쉽게 말하면 각각이 독립이라고 가정을 해도 p(x|y=강아지), p(x| y = 고양이) 를 비교하면 강아지 데이터들이라면 p(x|y=강아지) 가 높게 나옵니다. 비록 확률 값은 말도 안되게 나오겠지만, 그래서 Naive Classifeir를 사용한다고 합니다.

Discriminant classifier VS Generative classifier

그래서 Discriminatn clasifier와 Generative classifier를 비교해보면, Discrimination classifier의 경우 p(y|x) 를 직접 계산합니다. 당연히 아무 가정이 없다면 구할수 없습니다.그래서 이전에 배운 Logistic Regression에서도 " log odds가 선형적이다. " 라는 가정을 통해서 p(y|x)를 모델링할수 있었습니다.

그에 반해 Generative classifier의 경우 p(y|x)에 특정 가정을 두지 않고 베이즈 정리르 통해서 p(x|y)p(y)를 간접적으로 구하는 방법을 채택하였고, 이때 p라는 분포의 모양을 Gaussian으로 가정하면 LDA, QDA 를 얻을수 있습니다.

즉, p(y|x) 가정을 통해 직접 구할것인지, 혹은 간접적으로 베이즈 정리를 통해서 구할것인지에 대한 철학이 다르다고 할수 있습니다.

ROC

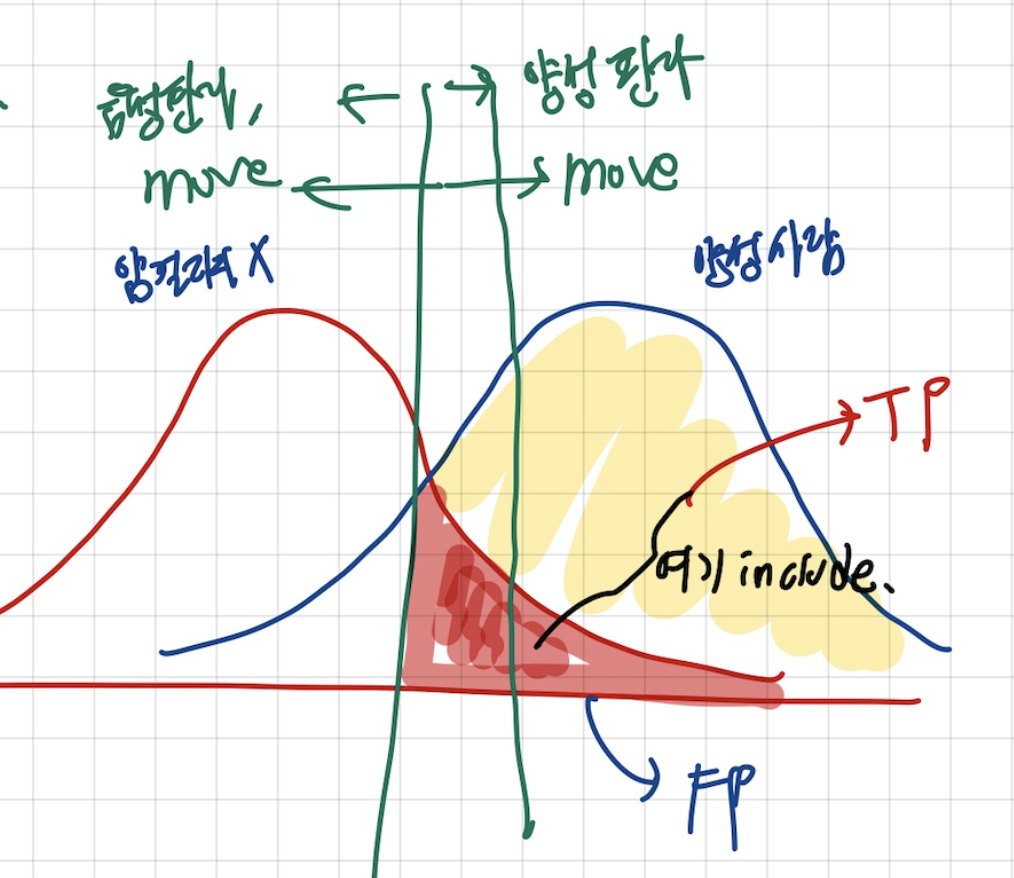
ROC 커브(Receiver Operating Characteristic Curve)는 이진 분류기의 성능을 임계값(threshold)의 변화에 따라 종합적으로 평가하는 대표적인 도구입니다. 분류 모델이 “양성”으로 예측하는 기준점을 높이거나 낮춤에 따라 실제 양성 샘플 중에서 올바르게 양성으로 판정하는 비율인 TPR(True Positive Rate)과, 실제 음성 샘플 중에서 잘못 양성으로 판정하는 비율인 FPR(False Positive Rate)이 어떻게 변화하는지를 계산해, FPR을 가로축에, TPR을 세로축에 찍은 곡선을 그립니다.

이 곡선이 왼쪽 위 코너(낮은 FPR, 높은 TPR)에 가까울수록 분류기가 “거짓 경보는 적게, 진짜 양성은 많이” 잡아내는 좋은 성능을 가진 것으로 볼 수 있습니다. 곡선 아래 면적인 AUC(Area Under the Curve)는 모델의 전반적 분류 능력을 하나의 숫자로 요약해 주며, 1에 가까울수록 완벽한 분류기를, 0.5에 가까울수록 무작위 추측 수준의 성능을 의미합니다.

예를 들어 암 진단 모델이라면, 낮은 임계값에서는 많은 환자를 암으로 분류해 놓고 많은 정상인까지 오진(FPR 증가)을 감수하며 TPR을 극대화하고, 임계값을 높이면 오진은 줄지만 놓치는 암 환자(TPR 감소)가 늘어나는 과정을 ROC 커브로 시각화해 최적의 균형점을 찾을 수 있습니다.