---

분류 모델은 종속 변수 y가 범주형일 때 사용하는데, 이를 구현하는 대표적인 방법은 먼저 선형회귀를 통해 실수값 $z=w^\top x+b$를 예측하고, 이 값을 시그모이드 함수

$\sigma(z)=\frac{1}{1+e^{-z}}$

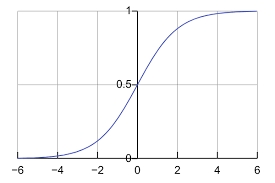
에 통과시켜 확률 $0\le\sigma(z)\le1$로 변환하는 것입니다. 시그모이드는 입력이 커질수록 1에, 작아질수록 0에 수렴하며 절대로 음수나 1을 넘어서는 값을 내지 않습니다. 이렇게 얻은 확률에 보통 0.5를 기준점으로 적용하여 $\sigma(z)\ge0.5$이면 클래스 1, 그렇지 않으면 클래스 0으로 최종 예측합니다.

만일 이진 분류 문제라고 가정을 하면 다음과 같이 수식으 전개해볼 수 있습니다.
$$ p(y=1\mid x)=\frac{1}{1+e^{-(\beta_0+\beta_1x)}} $$

$$ 1-p(y=1\mid x)=p(y=0\mid x) $$

해당 식을 풀어서 각 확률의 비료 표현을 하ㅏ고, 로그를 붙히게 되면 아래와 같은 식을 얻게 됩니다.
$$ \log\frac{p(y=1\mid x)}{1-p(y=1\mid x)} = \beta_0 + \beta_1 x $$
이 식에서 왼쪽 항을 log odds 라고 합니다. 따라서 Logistic Regression의 경우 log odds가 선형적일 것이라는 가정하에 나온 모델입니다.
결국 Logistic Regression은 " 입력이 한 단위 바뀔 때마다 ‘성공 대 실패 비율’이 일정한 배수로 바뀐다" 는 가정을한 classification model 입니다.

Linear Regression과 Logistic Regression

Liner Regression : "데이터들 사이의 관계 자체가 선형적일 것이다" 라는 가정을 한 모델

Logistic Regression : "Log odds 가 선형적일 것이다" 라는 가정을 한 모델

MLE for Logistic Regression

likelihood를 구하고 log를 붙히면 다음과 같은 식을 얻을 수 잇다.
$ℓ(β)=logL(β)= ∑^n_{i = 1}​[yi​logσ(zi​) (1−yi​)log(1−σ(zi​))]$ 그리고 해당 식에 대해서 $logσ(z)=−log(1+e−z)+z$ 식을 활용하여 정리를 해주면 다음과 같은 식을 얻을 수 있다.
$\sum_{i=1}^n \bigl[y_i - \sigma(\beta^T x_i)\bigr]\,x_i = 0$ 수식을 보면 Linear Regression과 다르게 바로 $\beta$ 값을 얻을 수 없습니다. 그래서 Logistic Regression의 경우closed-form이 존재하지 않는 솔루션입니다.
close-form이 존재하기 위해서는 MLE를 풀었을떄 $\beta$ 에 대한 2차식이거나 선형방정식 형태로 나와 $\beta$ 의 역행렬을 구해 바로 해를 구할 수 있습니다.
그렇지 않는 경우는 대다수의 머신/딥 러닝에서 활용하는 Gradient Descent 방법을 활용해서 최적의 솔루션을 찾는 방법을 이용하게 됩니다.

그리고 지금까지 이진 분류 문제에 대해서만 풀었는데, 이진분류에서 log odds 식을 활용해서 N개의 클래스로 확장한 개념을 사용하게 되면 결국 Softmax 함수를 얻을 수 있게 됩니다. 그래서 classifiation에서 각 클래스에 대한 확률값을 얻기 위해서 마지막에 softmax 함수를 사용해주게 되면 각 클래스가 모델에서 나올 확률 값을 얻을 수 있습니다.

$\mathrm{softmax}(z)_i \;=\; \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}}$