---

SVM 기본적으로 특정 데이터가 나올 확률값들을 전혀 사용하지 않고, 단순히 데이터 point들 끼리와 decision boundary 사이의 거리를 활용해서 데이터들을 분류하는 방법입니다.

처음 부터 SVM의 단점 부터 짚고 가겠습니다. SVM 의 가장 큰 단점은 오직 binary classification만 풀수 있다는 것입니다. 그래서 만일 Multi classification을 풀기 위해서는 여러 SVM을 one-to-many로 두고 푸는 여러개의 SVM을 사용해야 한다는 점입니다.

그래도 다소 기하학적인 접근을 가지고 있기에, 왜 decision boundary가 그렇게 생성되는지 이해하기 매우 쉽습니다.

SVM

우선 데이터 포인트들이 만약 $y = \beta_{0} + \beta_{1}x_{1} + \dots. + \beta_{p}x_{p}$ 로 정의 될 수 있다고 가정합시다. 그리고 $\beta_{0} + \beta_{1}x_{1} + \dots. + \beta_{p}x_{p} = 0$ 이 되는 hyper plane을 만들수 있습니다. hyper plane을 만드는 이유는 모든 지점이 0이 되는 hyper plane을 기준으로 위에 존재하면 양수값을 갖고, 아래 존재하면 음수 값을 같기에 이를 기준으로 데이터를 분류하게 되면 서로 다른 두 클래스를 구분할수 있기 때문입니다.

그래서 우리는 해당 hyper plane과 수직인 법선 벡터를 생성합니다. 그래서 만일 법선 벡터와 동일한 방향성을 가지고 있는 데이터의 경우 양수값을, 그렇지 않은 경우 음수값을 갖도록 설정할수 있습니다.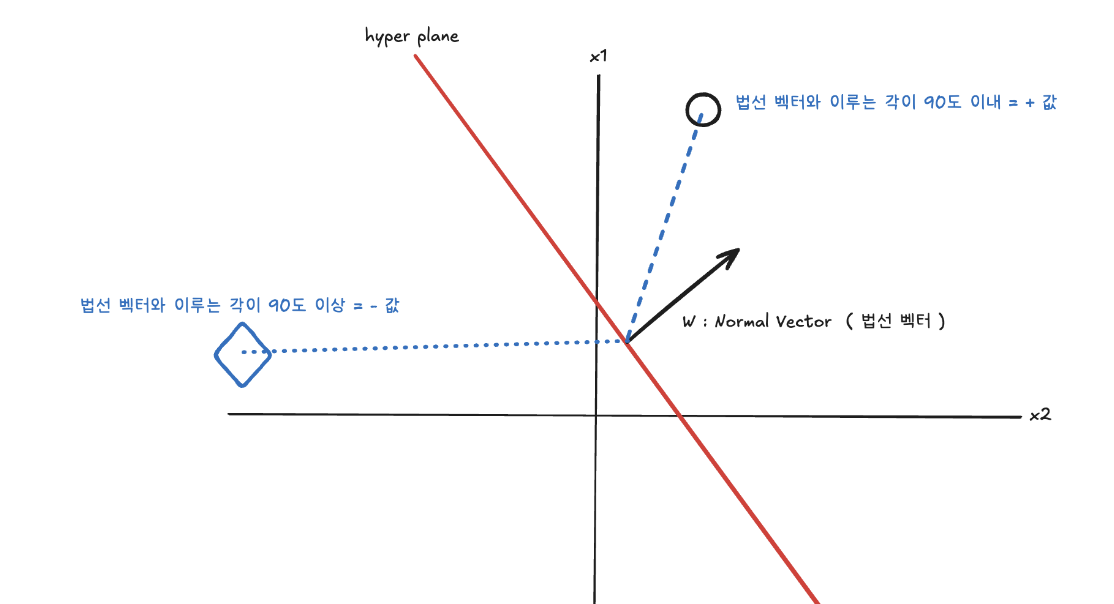

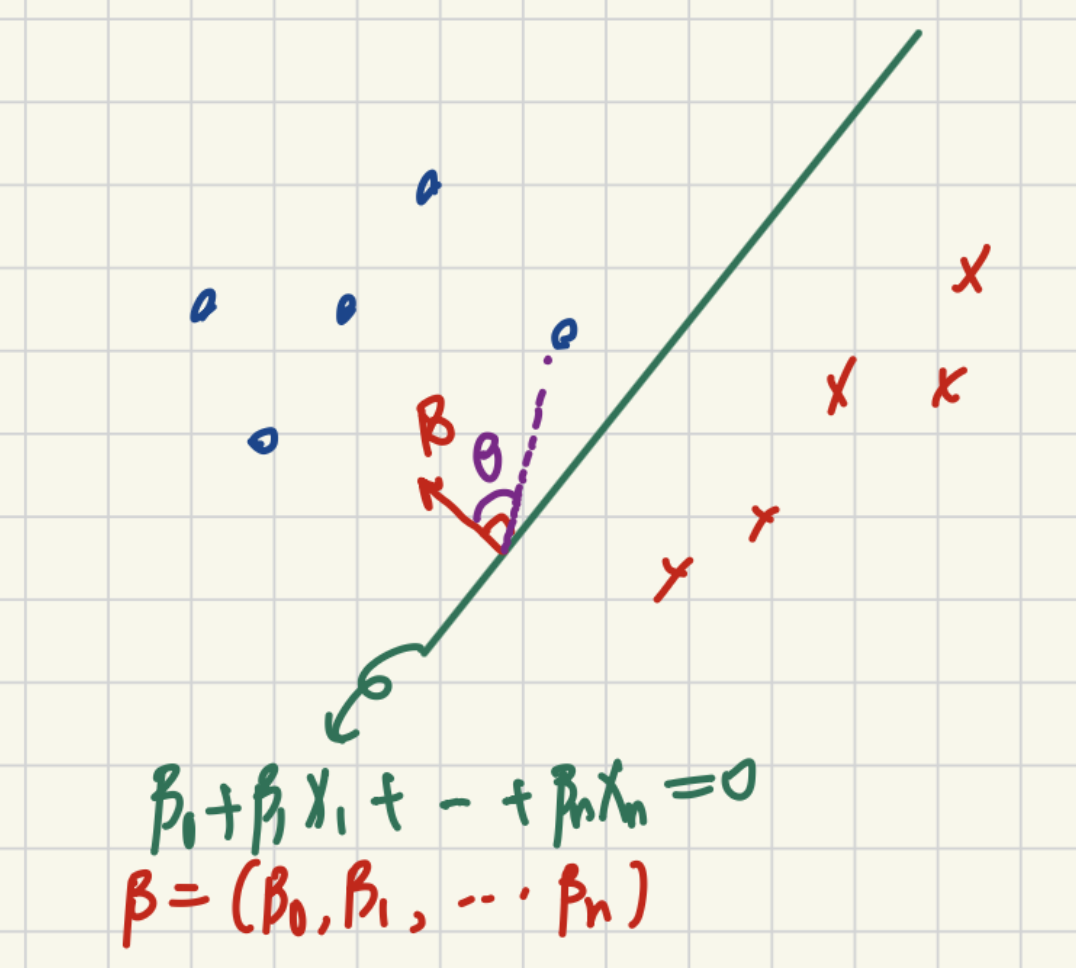
위고 우리는 Margine = hyper plane과 데이터들 사이의 거리 ( 가장 가까운 데이터 ) 를 Maximize 하고자 합니다. 즉, 2개의 클래스를 구분할떄, 최대한 잘 구분하는 hyper plane을 찾는것 입니다.

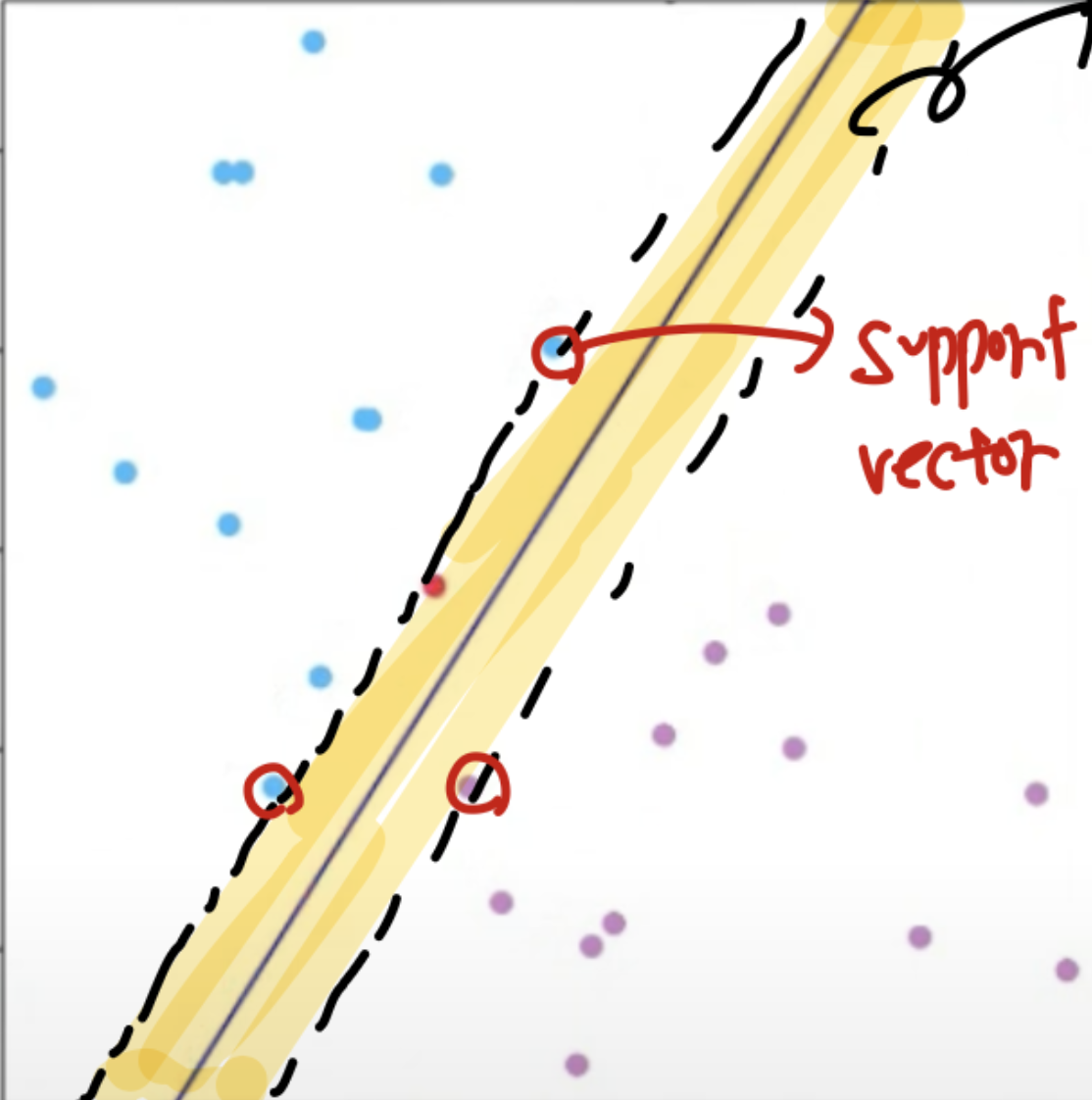
여기서 보라색이 hyper plane이고, 노란색으로 색칠된 부분이 Margine입니다. SVM의 목표는 해당 Margine을 Maximize하는 것입니다.

그래서 SVM의 목표를 식으로 정리해보면 아래와 같습니다.

M이라는 Margine을 최대화해야한다! 단, 각각의 $\beta = 1$ 로 크기가 영향을 주면 안되고, 모든 데이터와 hyper plane 사이의 거리는 최소한 Margine 보다는 크거나 같아야한다는 조건입니다.

그러기 위해서는 우리는 각각의 데이터들과 hyper plane 사이의 거리를 구할 수 있어야 합니다. 그래서 벡터를 2개의 성분으로 나눈 후 코사인 법칙을 적용하게 되면 아래와 같이 거리를 구할수 있게 됩니다.

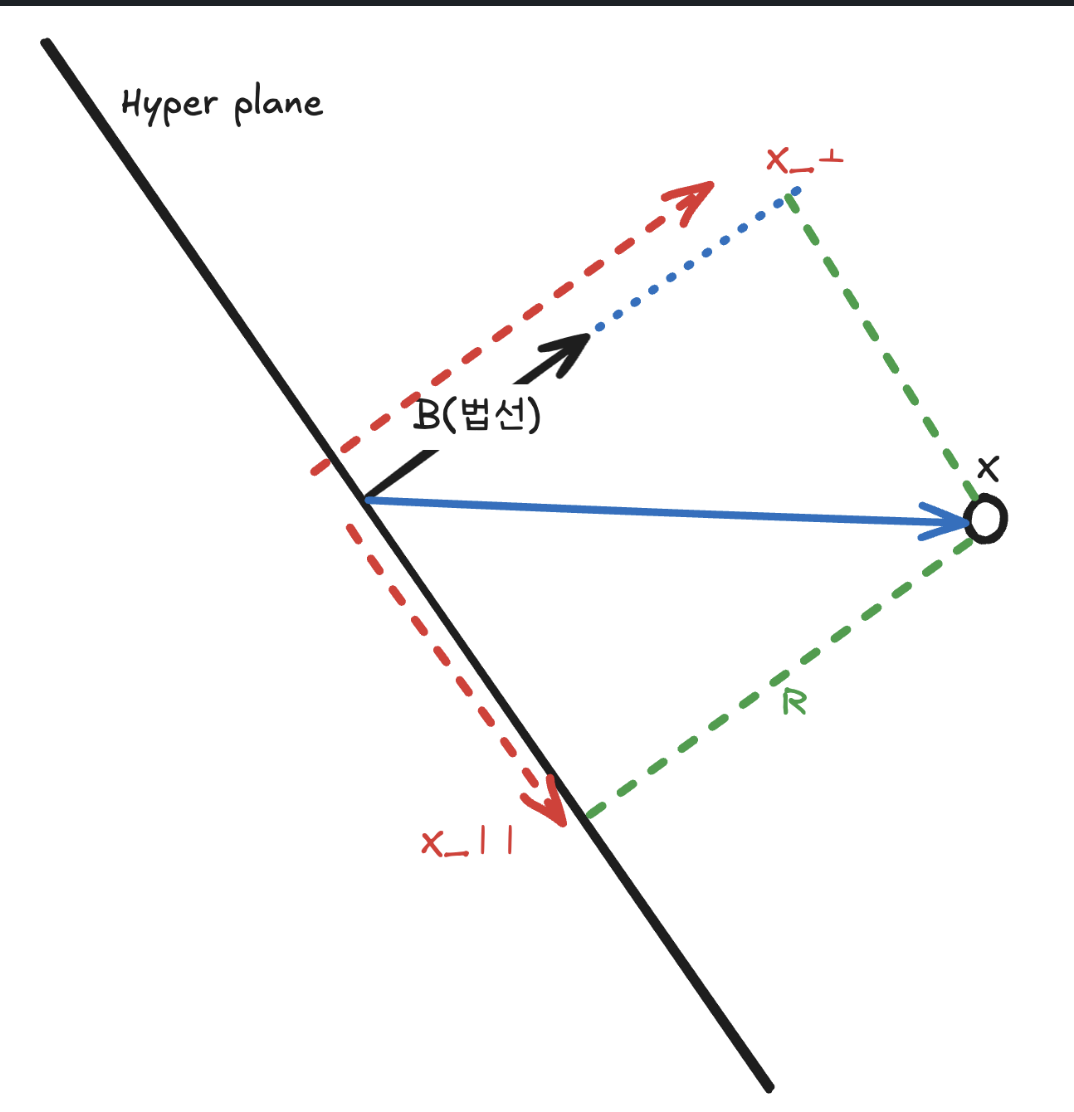
(1) x데이터와 법선 벡터를 내적하게 되면, 빨간색 그림처럼 x 벡터가 분해되게 됩니다.

(2) 하지만 $\boldsymbol\beta^T x_\parallel$ 의 경우 서로 수직이기 때문에 0인 값을 갖게 되어 사라지고, $x_\perp$ 는 법선의 크기로 정규화 해주고, 법선 방향의 성분을 곱해주는 식으로 정리해볼 수 있습니다.

(3) 그리고 Cos 법칙을 적용하게 되면 다음과 같이 적용이 가능하며 여기서 두 각은 0도 이기에 코사인 값이 1이 되게 됩니다.

(4)그래서 최종적으로 다음과 같이 정리해볼수 있습니다.

(5) 최종적으로 r 에 대한 식으로 정리해보면 아래와 같은 식을 얻게 됩니다.

그러면 이제 우리의 목표는 해당 거리를 최대화하는 것으로 치환해볼 수 있습니다.

즉, 해당 식을 보면 거리가 가장 가까운 데이터와의 거리를 최대화 해야합니다. 하지만 해당 문제를 최적화 하기에는 minimize, maximize라는 2개의 문제가 있어서 바로 풀기에는 적합하지 않습니다.

그래서 가장 가까운 point와의 거리가 1이 되도록 트릭을 사용하게 됩니다. 즉, 특정 $\alpha$ 값을 곱해서 표현할수 있습니다. ( 스칼라를 곱해도, 가장 가까운 점들의 순서에는 지장이 없기에 )

그래서 처음에는 아래와 같은 식을 통해서 최적화를 진행했어야 했습니다. ( 여기서 베타가 분모 -> 분자로 올라오면서 argmax -> argmin 으로 변경됩니다 )

하지만 가장 가까운 점과 hyper plane 사이의 거리가 1 이라는 제약조건을 넣게 되면 아래와 같은 식을 최적화 하는 문제가 되게 됩니다.

그리고 위의 식 조건에서 $y_i\,\beta^\top x_i \;\ge\;1\quad$ 식을 기하학적으로 살펴보면, 법선의 유클리드 거리 제곱을 최소화 하면서 데이터들과의 어떤 직선함수가 1보다 큰 것을 만족하라는것입니다. 그래서 데이터 수만큼의 직선이 생기고, 그중에서 1보다 큰 직선이 만드는 영역 중에서 $\beta$ 의 유클리드 거리가 가장 작은 점을 고른다는 의미로 해석이 가능합니다.

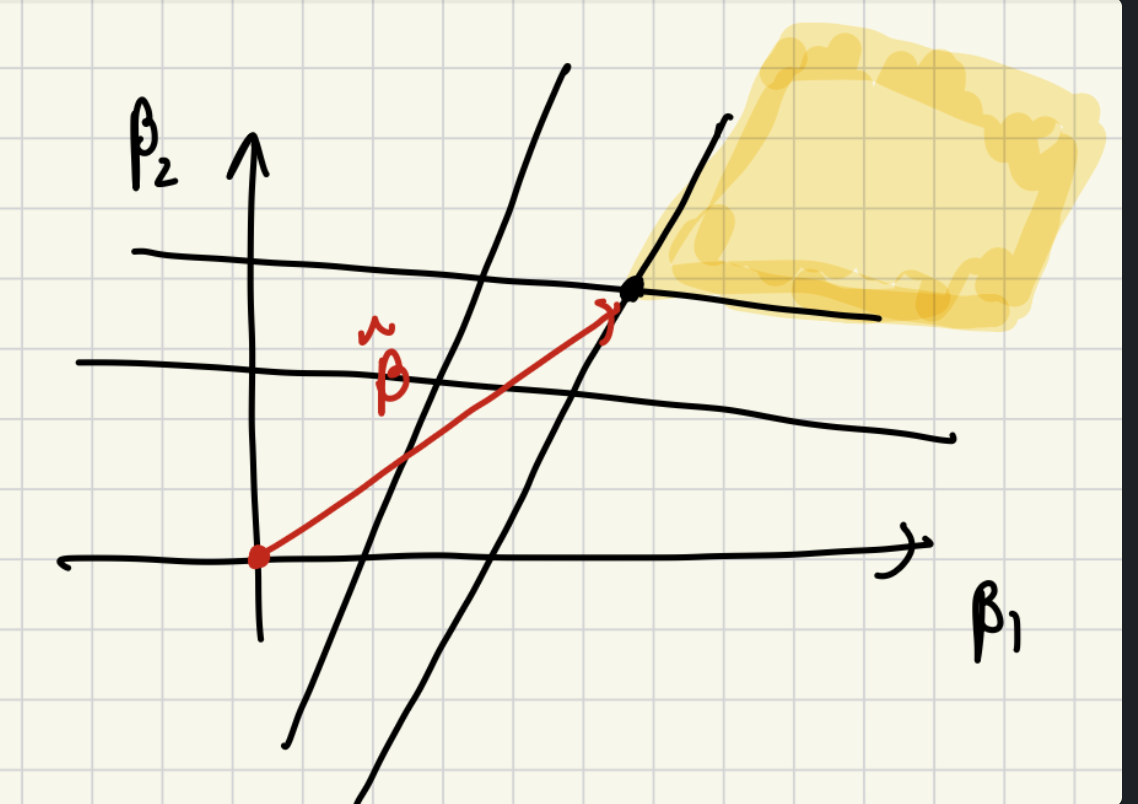
그림에서는 여러 직선 들이 나오고, 이들 중 > 1 을 만족하는 영역이 노란색 영역이기에, 베타의 길이가 가장 짧은 점은 표시해둔 점이 됩니다. 그래서 이를 만족하게 되면 결국 가장 가까운 포인트와의 거리가 최대가 되도록 할수 있습니다.

이를 풀기 위해서는 라그랑주 승수법과 KKT 조건에 대해서 알아야합니다. 하지만 간단하게 방정식을 사용해서 식을 구해보겠습니다 ( 라그랑주 승수법이란 최적화를 하는 경우 제약조건이 있는 경우 사용할수 있는 방법입니다 )

위의 식에 라그랑주 승수법을 도입하면 아래와 같은 식이 나오게 됩니다.

미분해서 각각의 값을 얻은 후 정리하면 아래와 같은 식이 됩니다.

그래서 아무튼 최종적으로 다음과 같은 식을 얻을수 있게 됩니다.

그래서 최종적으로 우리가 maximize를 해야하는 부분을 보면 아래와 같이 간단하게 해석할수 있습니다.

여기서 x들끼리 곱하는것은 실제 2개의 데이터가 같은 클래스라면 +, 아니라면 -가 나옵니다. 그리고 y끼리의 곱은 우리의 모델이 2개의 데이터를 동일한 클래스라고 예측하면 +, 아니면 - 입니다., 즉 yyxx가 의미하는건 모델이 잘 맞췄다면 +, 아니라면 - 값을 갖게 됩니다. 즉, 우리가 위의 식을 maximize하는게 목표이기 때문에 모델이 잘 맞췄다면 람닥밧이 0이 됩니다. 그리고 음수에 대해서만 곗나을 진행해주게 됩니다. 즉, 모델이 잘 예측하지 못하는, decision boudnary 근처의 값을 가지고 최적화를 한다는 것을 알수 있습니다.

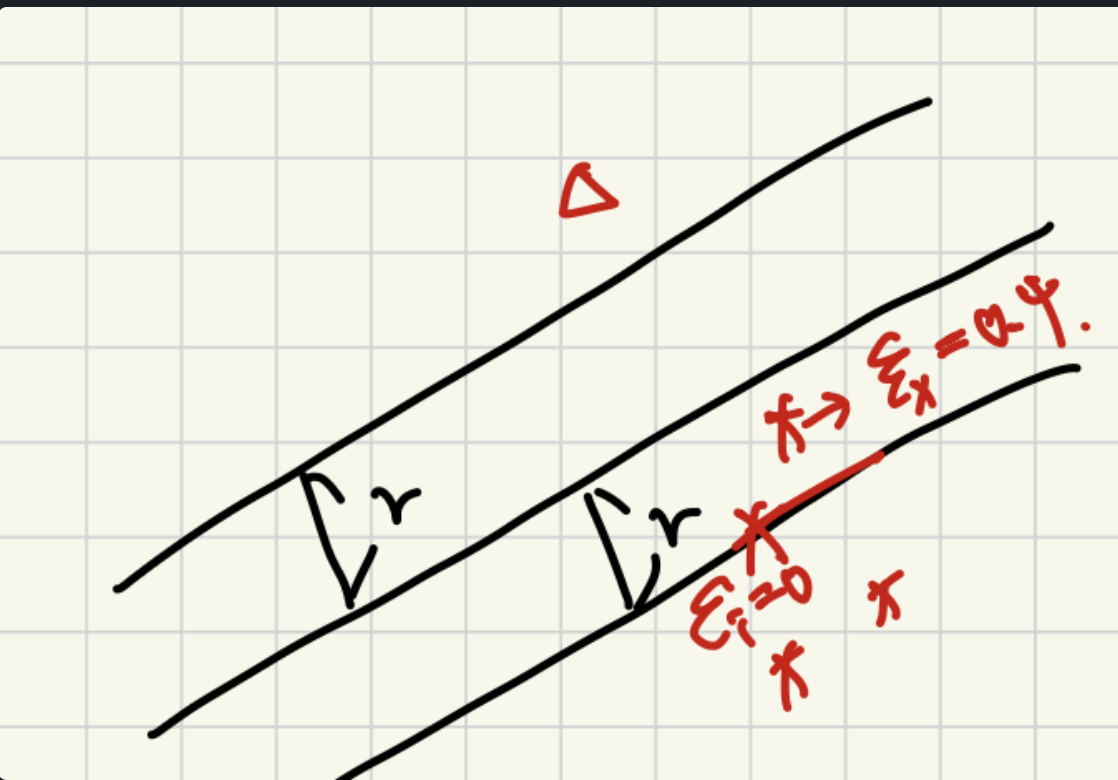
하지만 이렇게 하면 단순히 Margine만 늘리게 되면 데이터의 Noise에 취약하다는 점을 문제 삼아서 Margine 내부에 어느정도 데이터 들어가 보다 강건한 모델을 만들기 위해 soft margine이라는 개념이 도입되었습니다.

다음과 같이 기존의 Margine에서 추가 term을 둬서 어느정도 Margin 내부에 데이터가 들어오는 것을 허용해주게 됩니다.

여러 Loss들의 의미

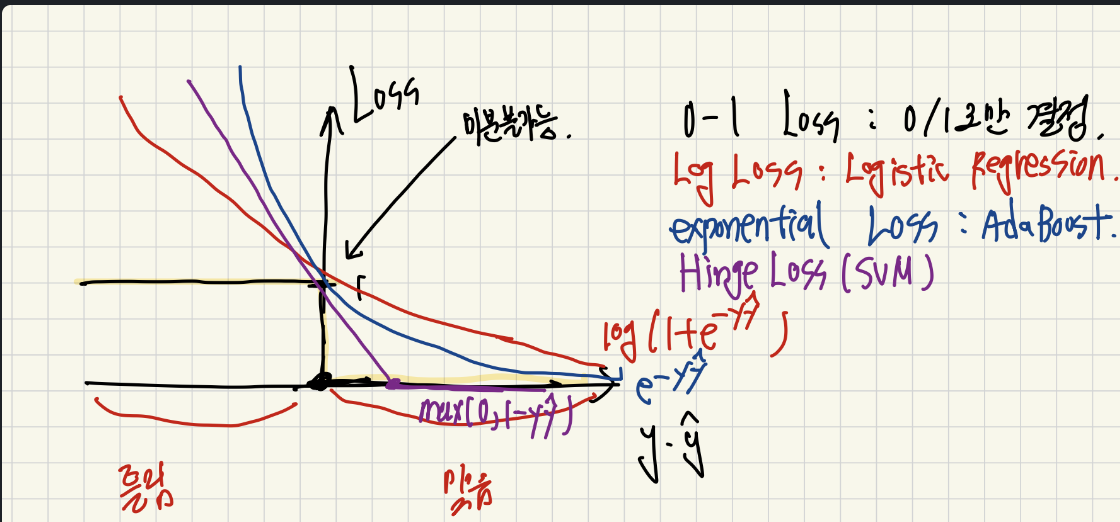
그리고 SVM에서 사용하는 것은 Hinge Loss를 어느 정도 맞게 되면 Loss = 0, 그리고 boundary 근처에 있다면 Loss를 주는 식을 사용합니다.

그리고 지금까지 배운 다양한 Loss들 도 보면 결국 모두 과정은 다르지만, 동일한 목표를 달성하기 위한 손실함수를 사용하고 있음을 확인할 수 있습니다.

+) Non-Linera SVM

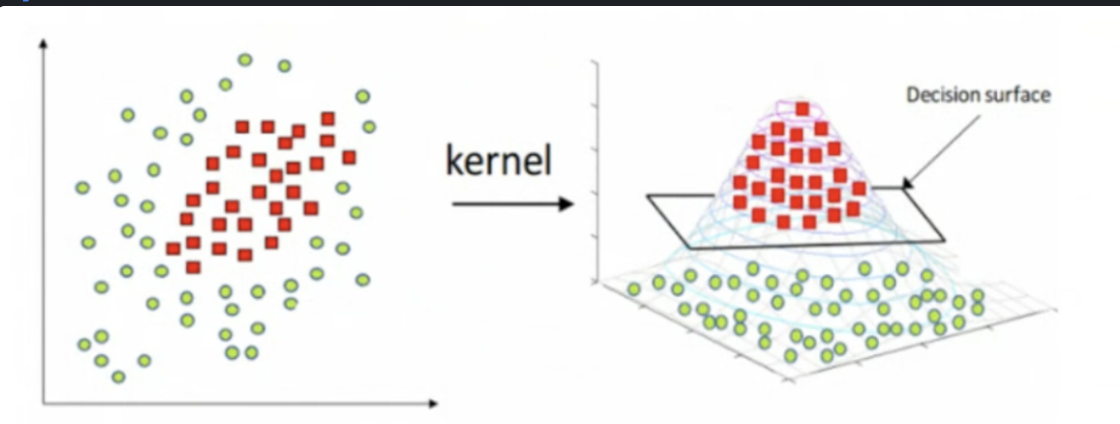
추가로 사진과 같이 Linear 하게 분리되지 않는 데이터들에 대해서는 kernel이라는 것을 도입합니다. kernel의 역할은 데이들을 마치 더 높은 차원으로 매핑 해서 분류하고 다시 원래 차원으로 되돌려 주는 역할을 수행합니다. ( 차원을 높히면 무조건 선형 분류가 가능해집니다 , 예를들어 N개의 데이터를 N차원에 두면 자연스럽게 모둔 차원이 분류가 가능하기 때문입니다. )