[ ML ] Linear Regression1

JSM0315·2025년 5월 12일

Machine Learning

목록 보기

1/9

Linear Regression

Linear Regression의 경우 데이터들간의 관계가 선형적일 것이다라는 가정하에 모델링하는 것을 의미합니다.
예를 들어 키와 몸무게가 선형적인 관계를 갖는다. 라고 가정을 하고 키와 몸무게 데이터를 가지고 이들을 설명하는 하나의 직선을 그리는 모델을 의미합니다.
그리고 Linear Regression의 경우 주로 아래와 같은 형태를 가지고 있습니다.

y = b_{0} + b_{1}x_{1} + b_{2}x_{2} + \dots + b_{n}x_{n}

그리고 LInear Regression에서 b값을 찾기 위해서는 주로 RSS라는 방법을 사용합니다. RSS는 단순히 실제 라벨값과 모델의 예측값 사이의 오차를 제곱해서 모두 더한 형식으로 표현됩니다.

RSS = \sum _ { i = 1 } ^ { n } ( y _ { i } - \beta _ { 0 } + \beta _ { j } x _ { i } ) ^ { 2 }

Why use squared error?

그렇다면 왜 오차의 제곱을 활용할까? 단순히 오차를 알고싶다면 4제곱이나 절대값을 쓰는등 다양한 방법론이 존재하는데, 굳이 제곱을 하는 이유가 뭘까??

이를 알기 위해서는 우선 IID와 likelihood 에 대해서 알아야한다.

IID

IID : Independent Identifically Distribution
IID를 가정한다는 말은 우리가 얻은 데이터들이 모두 독립이면서 동시에 동일한 분포에서 나왔다는 가정이다. 즉 , 동일한 주사위를 던져서 1 ~ 6사이의 값을 얻는 것을 의미한다. 만일 주사위 여러개를 던져서 나온 데이터들은 같은 분포가 아니기 때문에 IID가 아니게 된디.

Likelihood

Likelihood는 한국말로 가능도를 의미하고, 이는 여러개의 데이터들을 우리가 얻었을때 해당 데이터들이 나왔을 분포의 모수를 추정할수 있게 해주는 하나의 표현 방법이다.

조금더 쉽게 설명해보면, 우선 likelihood를 사용하기 위해서는 우리의 데이터들이 어떤 모양의 분포에서 나왔을지는 결정해줘야한다. 예를들어 Gaussian 모양을 갖는다고 가정해보자. 그러면 우리는 평균과 분산을 알아야 한다. 하지만 해당 데이터들이 나온 실제 평균과 분산은 우리가 알수 없다. 그렇기에 해당 분포의 평균과 분산을 구하기 위한 방법으로 가능도라는 함수를 사용하게 된다.

만일 IID를 가정하게 된다면 각각의 데이터가 나왔을 확률을 모두 곱한것이 해당 데이터들이 특정 모수를 통해서 나올 확률이 되게 됩니다.

$$ L(θ∣x{1},…,x{n}) = ∏pθ(x_{i}) $$

우리는 실제 모수의 값들을 알수 없으니, 가능도를 최대화 해서 이러한 분포에서 저런 데이터들이 나왔을 확률을 최대화 하고자합니다. 그리고 이러한 방법을 MLE 라고 부릅니다. ( Maximum likelihood estimation )

이를 최대하할때 우리는 미분을 사용해서 표현해야합니다. 그렇게 위해서 각 확률의 곲이 아니라 덧셈으로 표현하는게 유리하며 ( 기울기 소실이나 폭발 등의 위험에서 자유롭다고 생각된다...! ) 그래서 log를 붙혀 Log Likelihood를 최대하하는 식을 세울 수 있게 됩니다.

\ell(\theta \mid x_1, x_2, \dots, x_n) = \log L(\theta \mid x_1, x_2, \dots, x_n) = \sum_{i=1}^{n} \log p_\theta(x_i)

이러한 방법을 간단하게 적용해보면 베르누이인 경우와 가우시안인 경우 자연스럽게 각각의 모수는 평균, ( 평균, 분산) 이 나온다는 것을 알수 있습니다.

그래서 우리가 흔히 아는 정규분포는 결국 데이터들이 가우시안 분포에서 나왔다고 가정을 하고 MLE를 푼 결과 분포의 모수중 평균이 이 데이터들의 평균이 되고, 분산은 편차 제곱의 합이 됨을 확인할 수 있습니다.!

MLE를 미분하는 이유는 우리가 최대 값을 찾기 위해서 극대 혹은 극소를 찾고, 해당 값이 극대가 된다면 최대값이 되기 때문입니다. 그래서 우리가 원하는 변수에 대해서 미분을 하고 2번 미분한 값이 음수가 된다면 해당 값이 최적의 값이 됨을 확인할 수 있기 때문입니다.!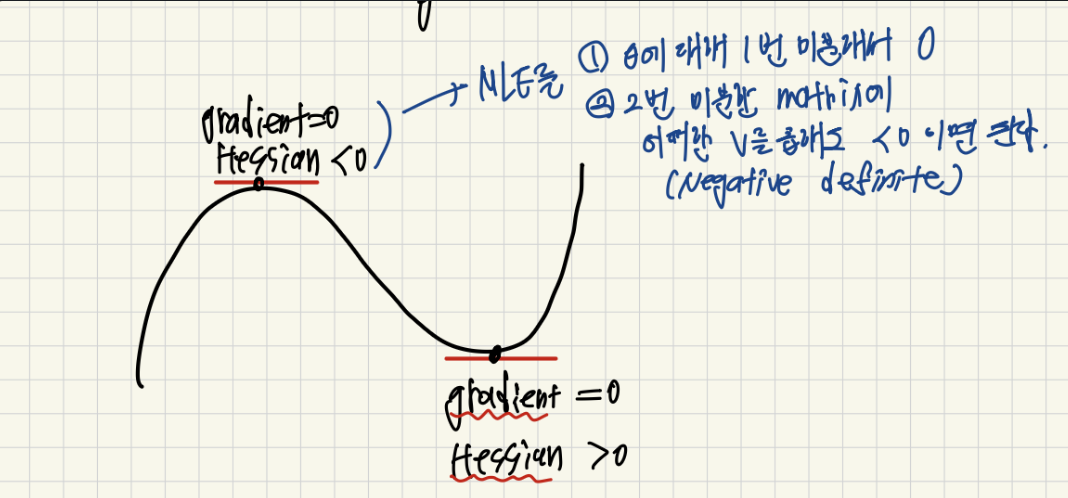

MLE for Linear Regression

그렇다면 우리가 위에서 구한 Linear Regression 모델에 MLE를 적용해보자.
우선 우리의 모델은 아래와 같이 정의될수 있습니다.

y = \beta_0 + \beta_1 x_1 + \cdots + \beta_n x_n + error

마지막에 항상 에러 텀이 붙게 됩니다. 이는 데이터를 샘플링 할때 어쩔수 없이 붙게 되는 노이즈입니다.
==Linear Regression 문제의 경우 저 error 가 평균이 0이거 분산이 시그마인 특정 가우시안 분포를 따른다고 가정을 하게 됩니다.==

그러면 전체적인 모델은 아래와 같은 가우시안 분포를 따르게 될것입니다.!

그러면 우리는 우리의 데이터들이 가우시안 분포를 따른다고 가정할수 있고 log likelihood 식에 x와 y를 대입해주면 아래와 같은 식을 얻을 수 있습니다.

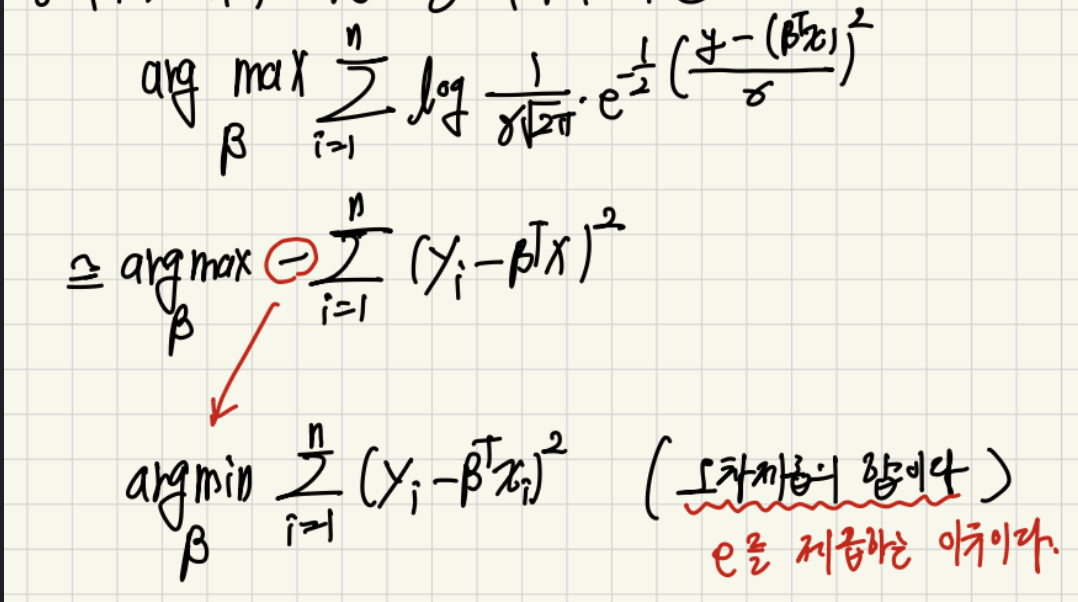
그리고 최종적으로 식을 정리해보면 실제값과 모델에서 예측한 값의 차이를 제곱하는 것이 최적의 베타를 구하는 식이 되게 됩니다.

===이렇듯 Linear Regression의 경우 IID 이고, 데이터의 샘플링 노이즈가 평균이0이고, 특정 분산을 갖는 가우시안 분포를 따른다는 가정하에 만들어진 모델이고, 이러한 모델의 최적값을 구하기 위해서 MLE를 한 결과 오차 제곱의 평균을 최소화 하는것이 최적의 베타값을 찾는 방법임을 알수 있었습니다.===

그리고 만일 x 값들이 행렬인 경우에는 아래와 같은 값을 얻게되는데,

\hat\beta = (X^T X)^{-1} X^T y.

위의 식은 OLS라고 X로 표현할수 없는 Y값을 최대한 근사하는 선형대수학에서 설명하는 최소제곱법과 동일한 식을 얻을 수 있습니다.

정리하자만 Linear Regression은 데이터들이 서로 선형적인 관계를 가지고 있음을 가정한 모델이고, 이때 데이터들이 IID하고 데이터 샘플링 에러가 특정 가우시안 분포를 따른다는 가정하에 모델링되었습니다.
그리고 MLE를 통해서 최적의 베타값을 구해보니, 사실 OLS 처럼 여러 데이터를 하나의 평면, 선으로 정사영 시켜주는 방법과 동일함을 알수 있었습니다.

Least Square ( Appendix )

만일 행렬 A가 (10 x 3 ) 크기를 갖고, full rank라고 가정을 해봅시다. 즉, 10차원에서 3차원을 span하고 있다는 것 입니다. 결국 해가 1개이거나 0개입니다.

span할 수 있는 3차원이 아니라 다른 차원에 값이 존재한다면 우리는 해당 값을 표현할수 없습니다. 하지만 해당 값과 최대한 유사한 값을 찾을 수 있습니다. 이렇게 span하지는 못하지만 span할 수 있는 차원에서 해당 값을 가장 잘 표현하는 것이 바로 Least Square 입니다.

행렬 A가 존재하고, A가 3차원을 span한다고 가정해봅시다. 그리고 b라는 벡터는 span가능하지 않은 위치에 존재합니다. 그리고 해당 b 벡터를 최대한 표현해보려고 합니다. 이를 시각적으로 나타내면 아래와 같이 표현할 수 있습니다.

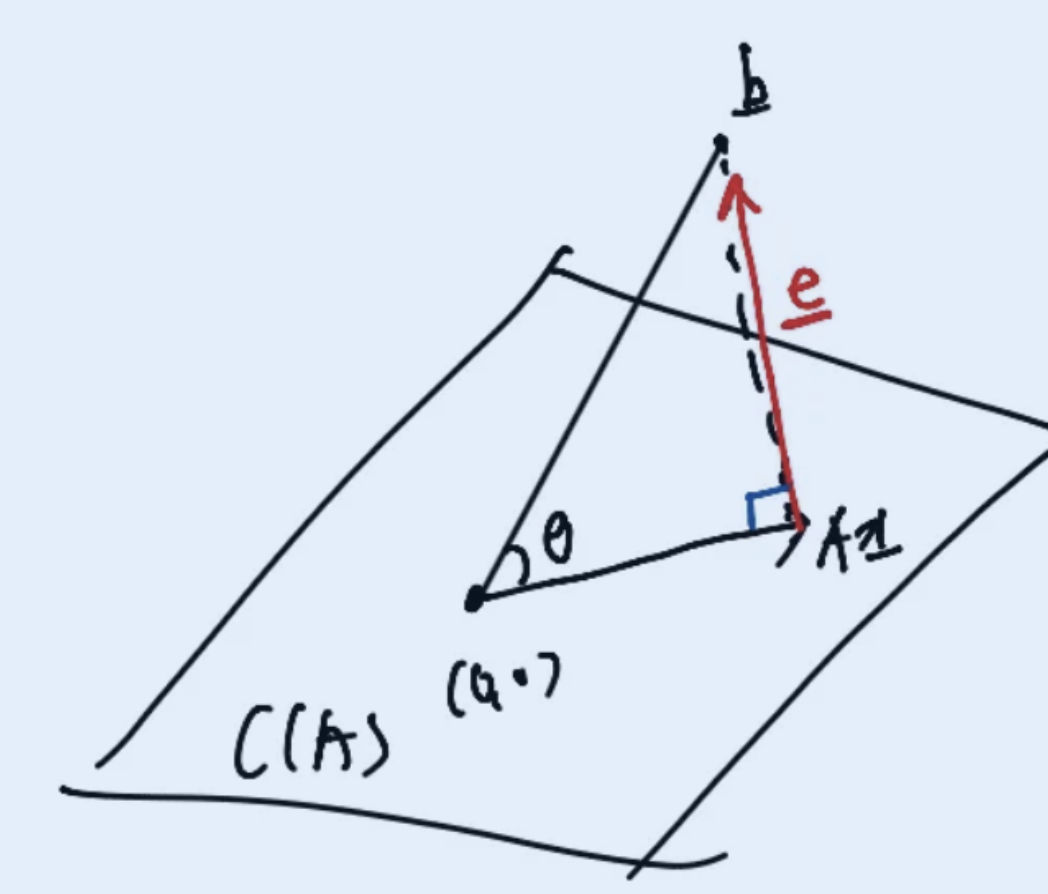
우리가 표현하고자 하는 벡터 b이고, 이를 가장 잘 표현하는 벡터가 A 행렬이 span할수 있는 차원 내에 존재하기에 $A\hat{x}$ 으로 표현하고자 합니다.

그렇다면 $A\hat{x}$ 와 벡터 b의 차이가 가장 작을때가 결국 b를 가장 잘 표현한다고 말할수 있습니다. 그래서 $b - A\hat{x}$ 를 최소화 하는 것이 가장 잘 표현하는것이고 결국 해당 값을 error vector라고 부를수 있습니다. 그리고 error vector가 최소가 되는 방법은 바로 $A\hat{x}$ 와 b 벡터가 서로 수직인 경우가 됩니다. 그래서 이를 수식으로 표현하면 아래와 같습니다.

min \{ error vectroc \} = (b - A\hat{x}) \perp A\hat{x}

그리고 수직인 경우 두 벡터의 dot product 값이 0이 되게 되고, 해당 식을 풀게 되면 결국 $\hat{x}$ 을 얻을 수 있게 됩니다.

과정은 아래와 같습니다.

(b - A\hat{x})^TA\hat{x} = 0

이 떄 $\hat{x} = 0$ 이 되는 경우를 제외한다면 결국에는 아래 수식을 만족해야 됩니다.

(b - A\hat{x})^TA = 0

아래 수식을 풀어서 보면 아래와 같습니다. ( 이항 한 다음에 transpose를 취해줍니다 양변에 )

(b^TA - \hat{x}^TA^TA) = 0

A^Tb= A^TA\hat{x}

이때 $A^TA$ 값은 정사각 행렬이고 Full Rank라는 가정하에 A 행렬은 invertable합니다. 그렇다면 결국 양변에 $(A^TA)^{-1}$ 을 곱해서 $\hat{x}$ 을 구할수 있게 됩니다.

\hat{x} = (A^TA)^{-1}A^Tb

위와 같은 식을 얻게 됩니다. 즉 위의 값을 만족할때 span가능한 3차원에서 b 벡터를 가장 잘 표현하게 됩니다. 그리고 $(A^TA)^{-1}A^T$ 에 단순히 b를 곱하면 해당 값을 얻을 수 있기에 $(A^TA)^{-1}A^T$ 을 projection matrix 라고 부른다고 합니다.

최종적으로 우리가 얻고자 하는 벡터는 $A(A^TA)^{-1}A^Tb$ 가 되게 됩니다.

Least Square의 경우 예를들어 특정 벡터를 선형변환하고 특정 noise가 추가되는 경우 해당 벡터를 다시 생성할때 주로 사용된다고 합니다. 즉 noise 처럼 되돌릴 때 표현할수 없는 경우 최대한 비슷한 값을 찾도록 하는 방법입니다.

JSM0315

누구보다 열심히

다음 포스트