---

Unsupervised Learning이란 데이터의숨겨진 패턴을 찾는 학습 방법입니다. 데이터에 대한 라벨을 지정하지 않기에, 동일한 데이터라도 사용자가 어떠한 목적으로 데이터를 사용하느냐에 따라서 다양한 방법으로 활용될 수 있습니다.

Unsupervised Learning은 주로 Clustering 문제를 풀게 됩니다. Clustering이란 데이터들 사이의 유사도를 측정하여 비슷한 데이터들 끼리 group을 형성해주고, 다른 데이터들끼리는 분리되도록 해주는 방법입니다. 그렇기에 데이틀 끼리 얼마나 유사한가?? 를 측정해주는 Metric 또한 정해줘야합니다.

그 중 가장 대표적인 방법인 K-Means 방법에 대해서 소개하겠습니다.

K-Means

k-means 알고리즘은 Bottom-up 방식을 사용한 Hierachical clustering 방식입니다. 즉, 맨 처음 각각의 데이터들은 각각의 group을 형성합니다. 그리고 각 그룹들 끼리의 유사도를 측정하고 특정 threshold를 넘는 gropu들은 하나의 group으로 묶어줍니다. 처음에는 큰 threshold를 사용하고, 점진적으로 threshold를 낮춰가는 전략을 주로 사용한다고 합니다.

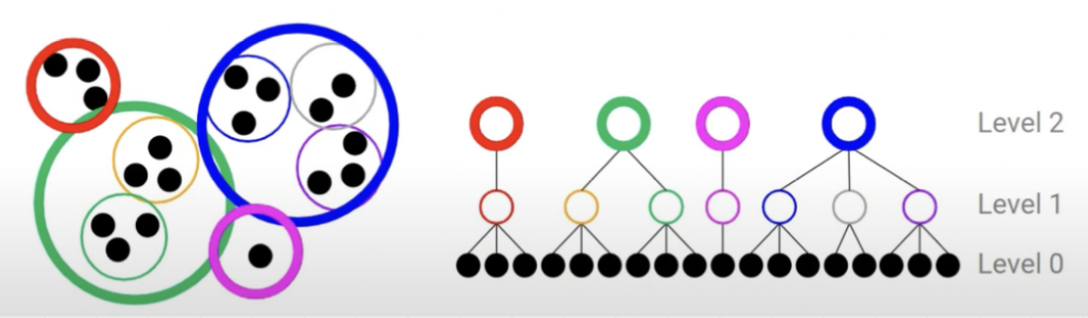
그리고 2개 이상의 데이터를 갖는 그룹은 해당 그룹의 대표값을 평균으로 사용하여 다른 그룹과 비교를 한다고 합니다.

그리고 더이상 모든 그룹의 평균이 변화하지 않는 경우 그룹화를 종료하고, 최종 그룹을 얻을 수 있습니다.

group의 손실은 동일 그룹의 데이터들과 대표값과의 MSE를 사용한다고 합니다. K-means의 경우 모든 데이터의 모든 조합을 다 살펴볼 수 있기애 반드시 끝나는 알고리즘입니다. ( 비록 모든 경우를 다보는 경우는 극히 드뭅니다 )

그리고 K 값을 어떻게 설정하느냐에 따라서 결과 또한 달라지게 됩니다. 그래서 K값을 어떻게 정해야하는지에 대해서는 여러개의 K에 대해서 진행을 하고, 적절한 ELBOW point를 선택해야합니다. K가 많으면 많을 수록 당연히 Loss는 줄어들게 됩니다 ( 데이터 갯수 = k 가 된다면 손실이 0이되기 때문입니다 ). 그래서 자원과 정확도 tradoff관계에서 적잘한 k를 찾는게 중요합니다.

Dimension Reduction

그리고 unsupervised Learning의 한종류로 Dimenstion Recution이 있습니다. 과연 우리가 어떻게 데이터들의 차원을 줄일수 있을까요? 흔히 모든 값들이 데이터를 표현하는데 중요하다고 생각하지만 Data Manifold에 의하면 D 차원의 영역에서 데이터를 나타내는 영역은 특정 구역에 밀집되어있다고 합니다.

그말은 즉, 특정 데이터가 밀집한 차원으로 데이를 차원해도 정보를 거의 잃지 않으면서 연산량을 획기적으로 줄일수 있음을 암시합니다. 하지만 차원을 축소할때도 각 데이터들 사이의 분포 거리는 비례하게 유지해줘야합니다.

그리고 Dimenstion Reduction의 가장 대표적인 예시는 바로 PCA입니다.

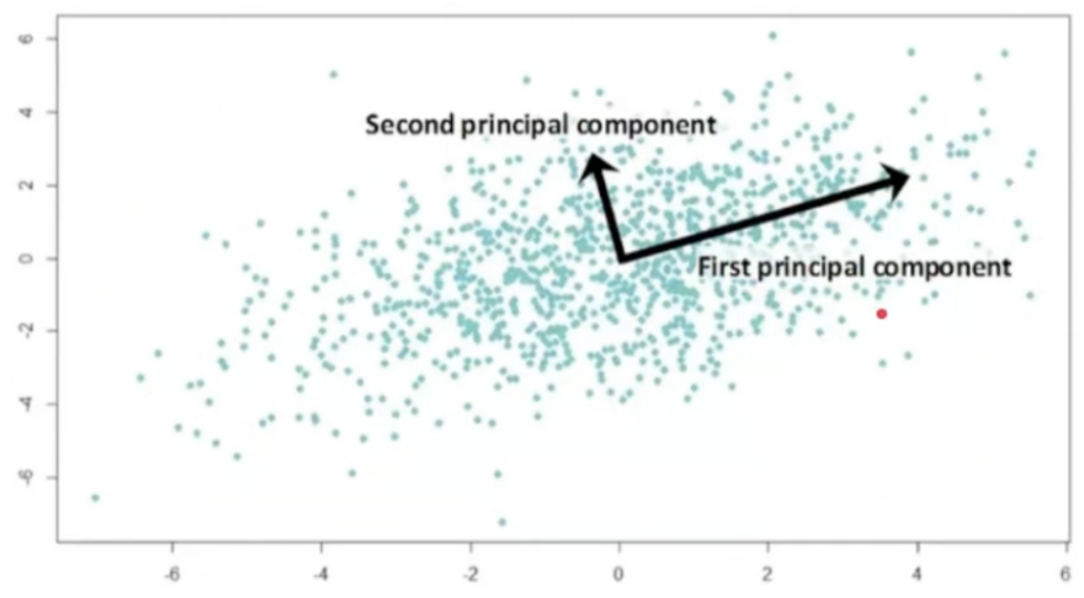
PCA에 의하면 데이터를 가장 잘 설명하는 방향은 모든 데이터들의 분산 방향이고, 그 다음은 분산 방향에 수직인 벡터가 됩니다. 그 이유는 PCA를 라그랑주 승수법으로 풀어주게 되면, 결국 공분산과 고유값의 식으로 표현되며, 고유값을 기준으로 가장 큰 고유값을 갖는 방향이 바로 데이터를 가장 잘 나타내는 방향이 됩니다. 그리고 모든 고유값들은 수직이기에, 다음 벡터는 당연히 가장 잘 나타내는 벡터와 수직일 수 밖에 없게 됩니다.

이를 통해서 데이터의 정보를 최대한 잃지 않으면서 연산량을 줄일수 있는 것이 Dimension reduction 방법입니다.

Appendix) PCA

PCA(Principal Component Analysis) 는 데이터를 가장 잘 설명하는 vector를 찾는 방법입니다.

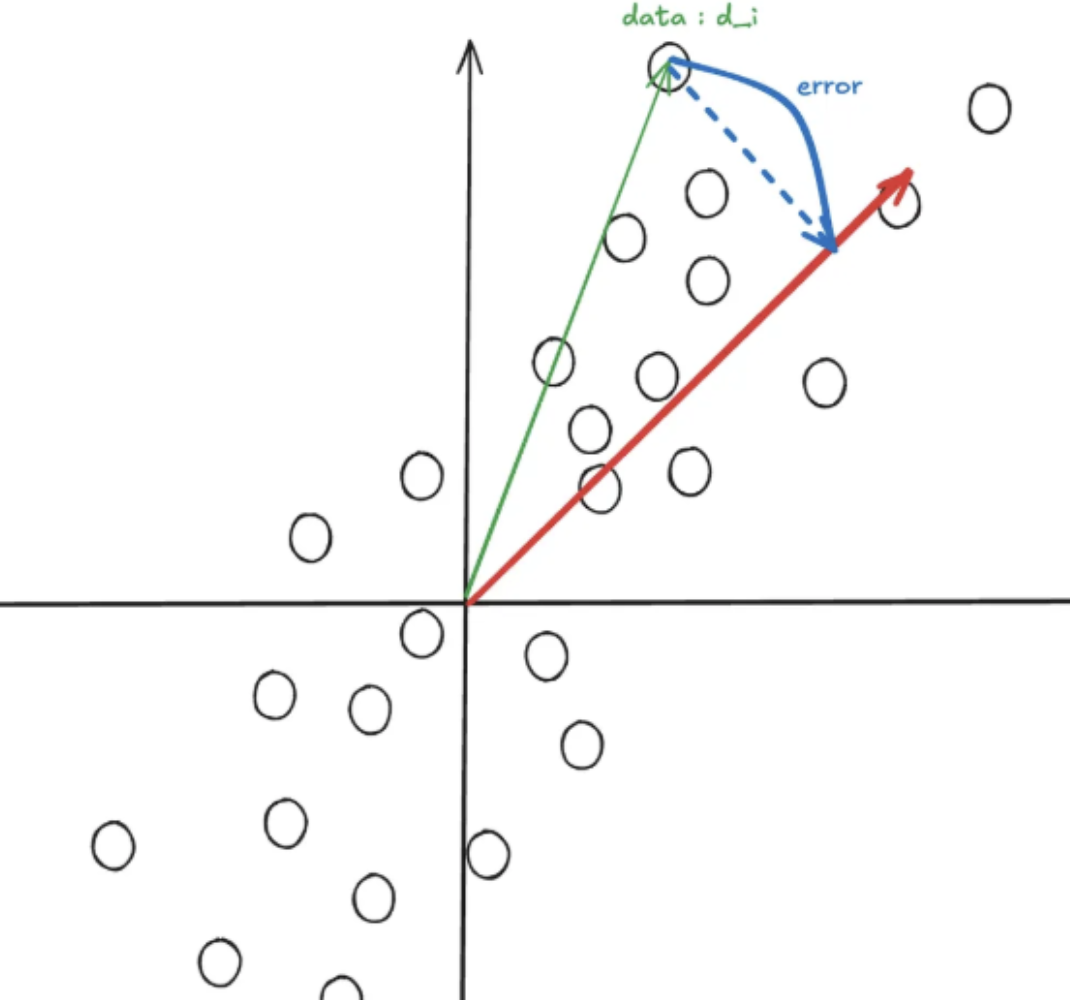
다음과 같이 해당 데이터를 가장 잘 설명하는 빨간색 vector가 존재한다고 합시다. 이때 임의이 x에 대해서 빨간 vector와의 차이를 구하게 되면 파란색처럼 error vector를 구할수 있게 됩니다. PCA는 이렇게 error vector의 크기를 최소하하는 방법입니다.

이를 수식으로 표현해보면 아래와 같이 표현할 수 있습니다. 이떄 우리가 모든 데이터 $d$에 대해서 모듬 데이터들의 평균을 빼서 평균 = 0 으로 만들기 위해서 $\tilde{d} = d_i - \bar{d}$를 구했다고 설정을 합니다. 그리고 주성분 벡터를 $U$ 벡터라고 가정을 하게 되면 자연스럽게 error vector의 크기는 $\|d_i - d_i^TUU\|_2^2$ 다음과 같이 정의할 수 있습니다. 그리고 만일 U 벡터 자체가 너무 작아지게 되면 데이터와는 상관없이 error vector의 크기가 작아지게 되기에 U벡터의 크기는 1로 가정을 하게 됩니다. 즉 아래와 같은 수식을 풀게 됩니다.

${1 \over n } \sum^n_{i=1}\|d_i - d_i^TUU\|^2_2$

위의 식을 minimize 하게 됩니다. 그리고 가정으로 아래와 같은 조건을 만족해야합니다.

$\text{S.T)} \|U\|_2^2 = 1$

해당 식을 만족해야합니다. 우선 위의 mimize해야하는 식을 전개하면 아래와 같은 식을 얻을수 있게 됩니다.

$-U^T {1 \over N} \sum^n_{i-1}(\tilde{d_i} - \tilde{d})(\tilde{d_i} - \tilde{d})^TU$

여기서 중요한 것은 바로
$(\tilde{d_i} - \tilde{d})(\tilde{d_i} - \tilde{d})^T$

값이 결국 covariance matrix가 된다는 것입니다.

즉, covariance를 최대화 하는것이 결국 해당 식을 최소화하는 방향이라는 결과를 얻게 됩니다. 추가적으로 covariance matrix의 경우 symmetric matrix입니다.

그래서 PCA는 데이터의 분산이 가장 큰 방향을갖게 되는것 입니다.

그리고 마저 해당 식을 풀기 위해서는 Lagrange multiplier를 사용해서 풀수 있습니다. 왜냐하면 U 벡터의 길이가 1이어야 하는 가정이 필요하기 때문입니다.

라그랑주 승수법을 통해서 해당 식을 풀게되면 $R_dU = \lambda U$ 라는 식을 얻게 됩니다. ( $R_d$는 covariance matrix를 의미합니다 ) 즉, PCA는 결국 eigen vector중에 존재하게 됩니다. 그렇다면 우리는 조건이 있는 최적화 문제를 풀었으니 해당 값을 만족하기 위해서

( $-U^T {1 \over N} \sum^n_{i-1}(\tilde{d_i} - \tilde{d})(\tilde{d_i} - \tilde{d})^TU$

해당 값을 minimize말고 max로 풀었습니다. ) 조건이 만족하는 값 내에서 가장 큰 값을 골라야합니다. 이는 곧 가장 큰 eigen value를 갖는 eigen vector가 됩니다.

최종적으로 PCA는 convariance 행렬에서 가장 큰 eigen value를 갖는 eigen vector가 되고, 이는 결국 covariance를 최대화하는 방향입니다. 그리고 그 다음으로 데이터를 가장 잘 설명하는 vector는 다음으로 큰 eigen value를 갖는 eigen vector가 됩니다. 그리고 covariance maxtirx는 orthogonal matrix이기에 자연스럽게 모든 vector들이 직교하게 됩니다. 그래서 2차원에서 PCA를 구할때 두번째로 데이터를 잘 설명하는 벡터가 데이터를 가장 잘 설명하는 벡터와 수직 관계를 이루게 됩니다.

정리

PCA는 데이터를 가장 잘 표현하는 vector를 찾는 문제이다. 그래서 데이터와 vector들사이의 에러를 줄이기 위해서 식을 전개해보면 결국에는 covariance를 최대화하는 방향으로 가야 error를 최소화할수 있습니다. 그리고 라그랑주 승수법을 통해서 식을 풀게되면 최적의 vector들이 바로 covariance matrix의 eigen vector들이고, 그중 가장 영향력이 큰 vector는 가장 큰 eigen value를 갖는 eigen vector가 되게 됩니다.