Lecture 10
Decision Trees
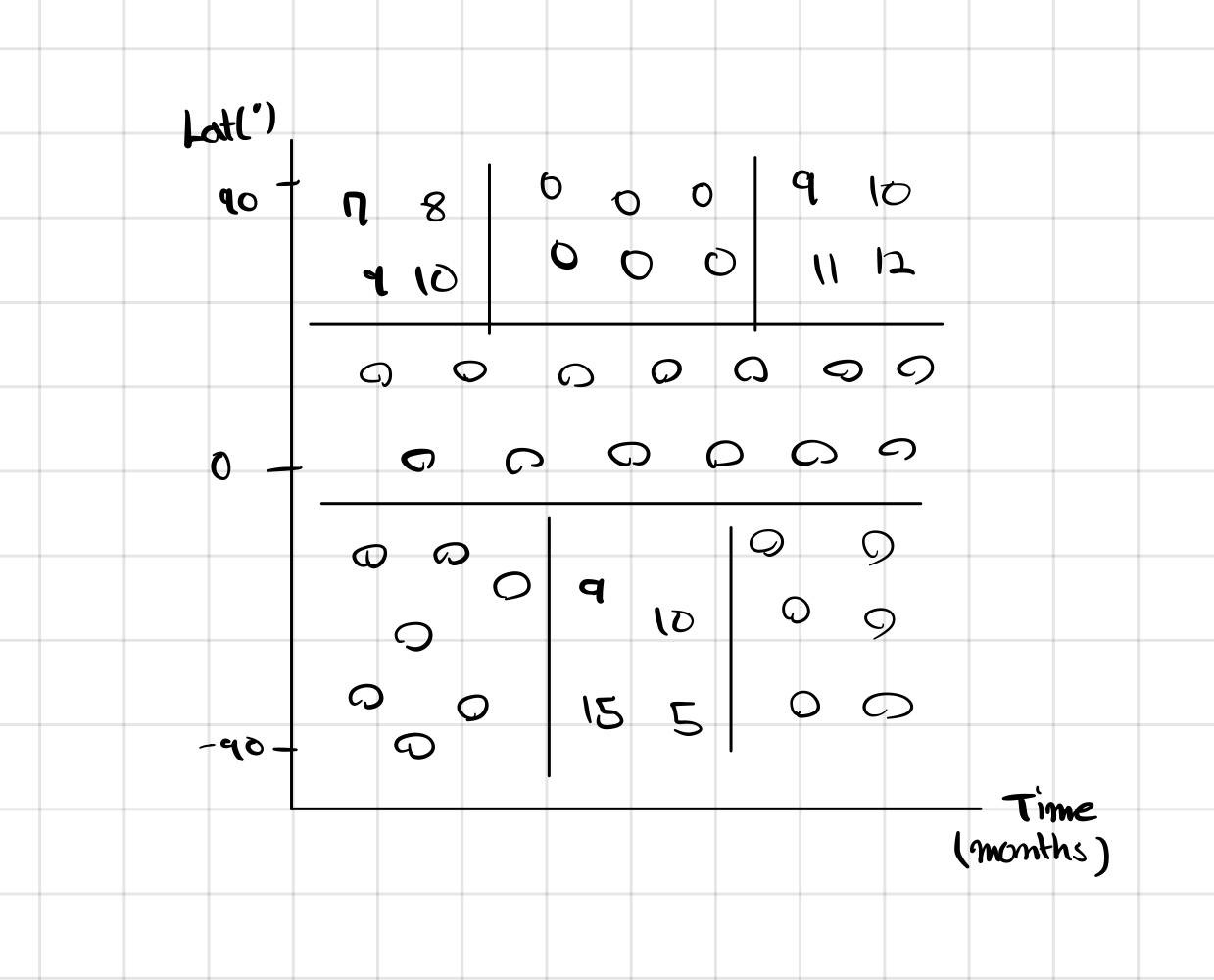
우선, 시간과 위도에 따른 스키를 탈 수 있는지 없는지를 알려주는 classifier를 만들어 보면 다음과 같다.
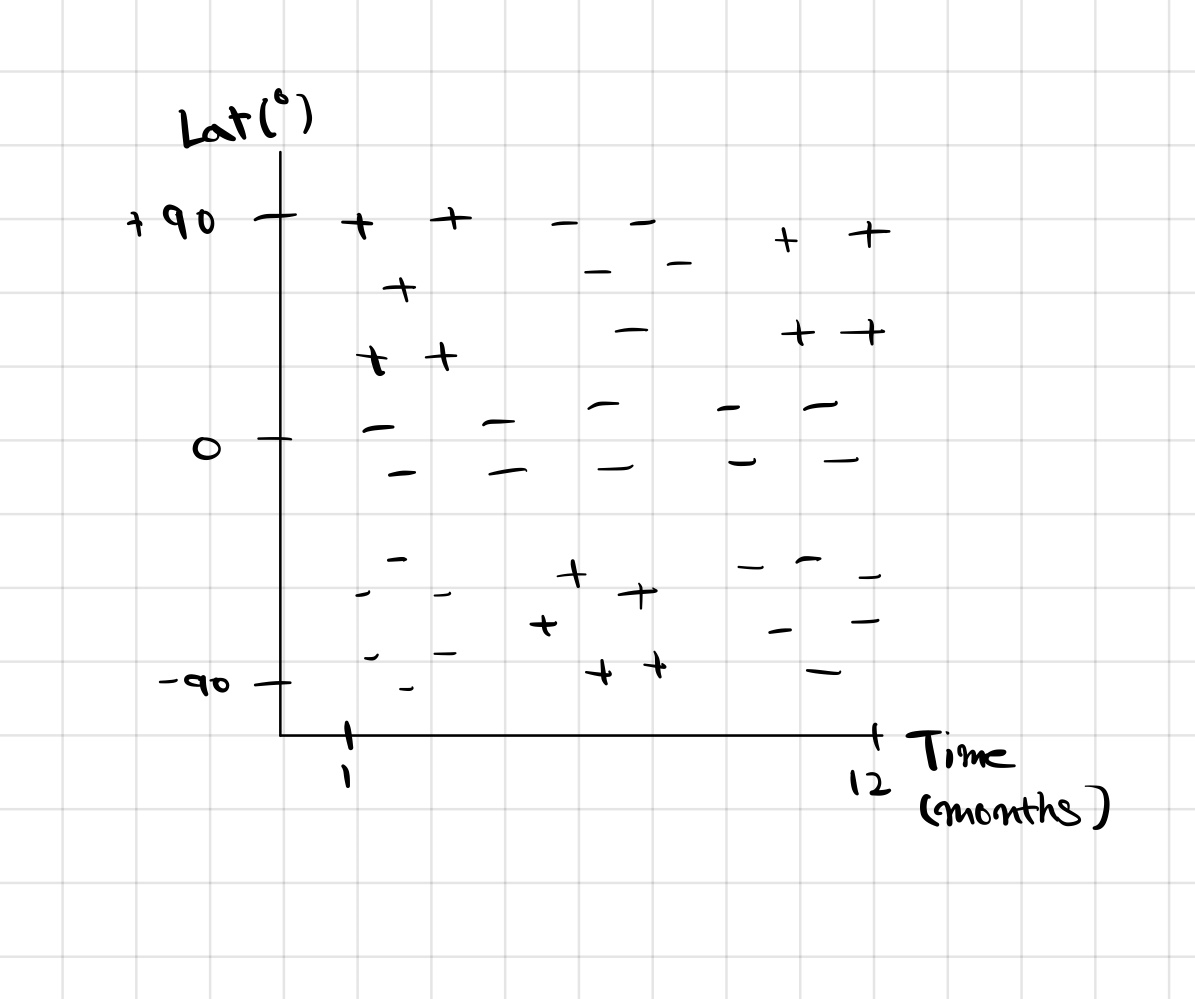
이것을 +와 -로 구분하기 위해서 아마도 SVM이나 Kernel을 생각할 수 있다.
하지만 Decision Tree를 사용하면 자연스럽게 가능하다.
Descion Tree는 기본적으로 다음 성질을 가진다.
- Greedy
- Top-Down
- Recursive
- Partitioning
이 방식은 기본적으로 전체 영역에서 시작해 천천히 분류해 나간다. (Top-Down) 또한, 각 단계에서 가능한 최선의 분할을 선택하려 한다. (Greedy) 또한, 분류를 한 다음 다시 그 분류된 부분을 다시 분류를 하게 된다. (Recursive)
예로 다음과 같은 질문이 가능하다. 위도가 30도 이상인가?
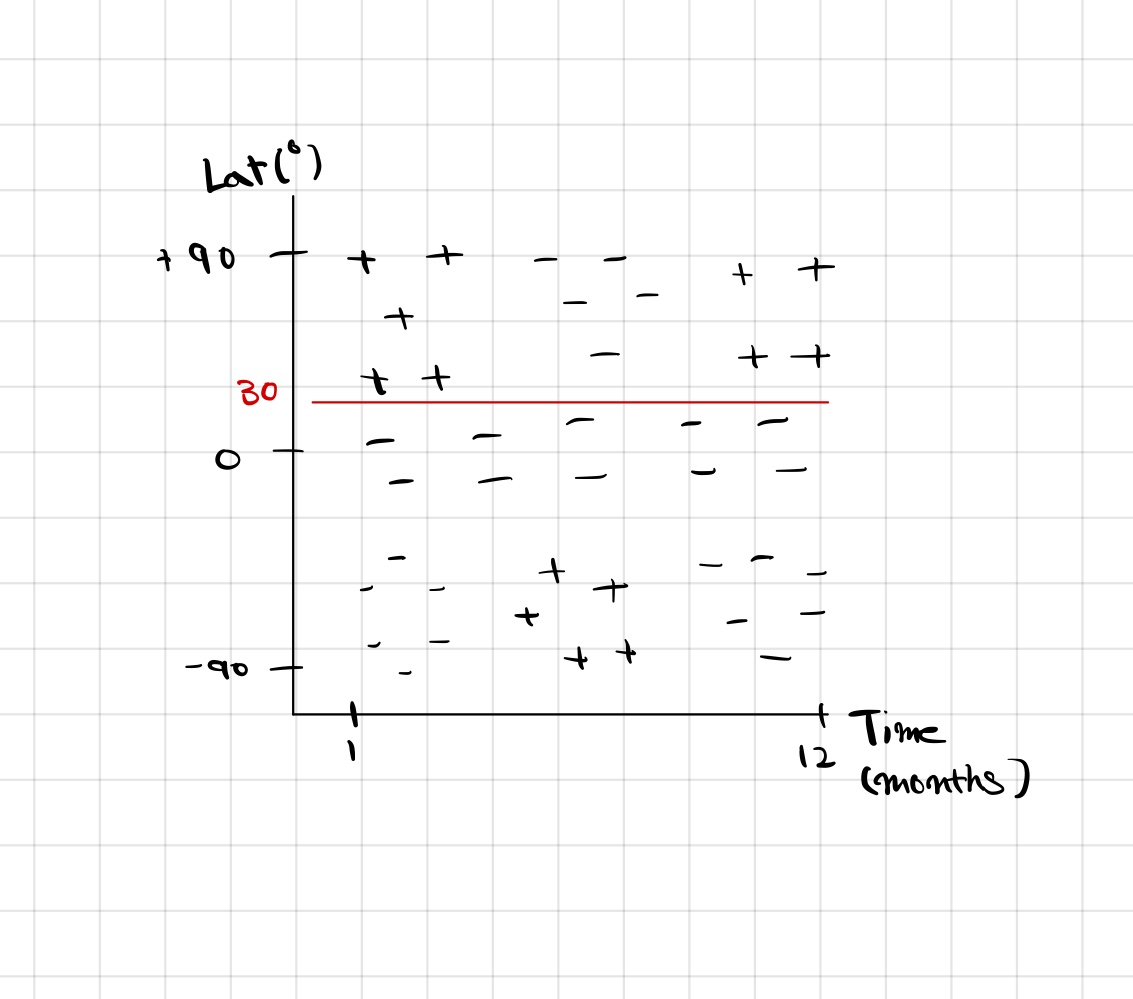
이 질문에 의해 왼쪽 그림과 같이 두 부분으로 분류 된다.
이제 위도가 30도 이상인 부분에 대해서 또 다시 새로운 질문을 할 수 있다.
Month가 3보다 작은가?
Month가 3보다는 크고 6보다는 작은가?
이런 재귀적인 질문들을 계속해서 하다 보면 이 전체 영역은 결국 개별 영역으로 분류할 수 있게 된다.
이를 Region 와 분할 지역로 일반화 할 수 있다.
이런 분할을 선택하기 위해서 우선 Region에 대한 손실을 정의해야한다.
이는 세분화 한 모든 Region, 지역에 대해 가장 일반적인 class를 예측하는 것이라 할 수 있다. 이런 Loss를 최소화 하는 것이 목적이므로 다음을 생각할 수 있다.
이때, 는 이미 정의되어 있는 값이므로, 결국 자식 지역의 손실을 최소화 하는 것과 같다.
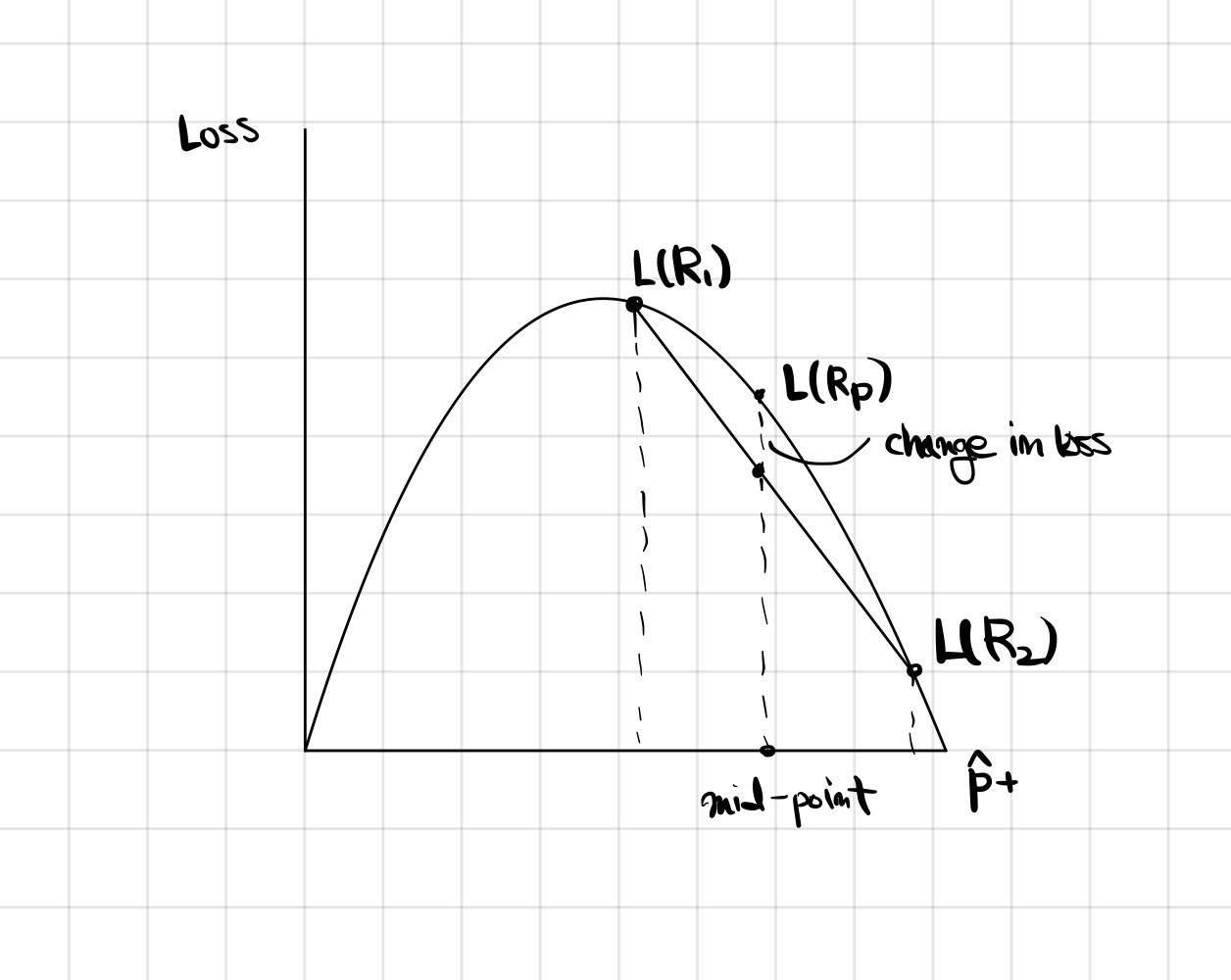
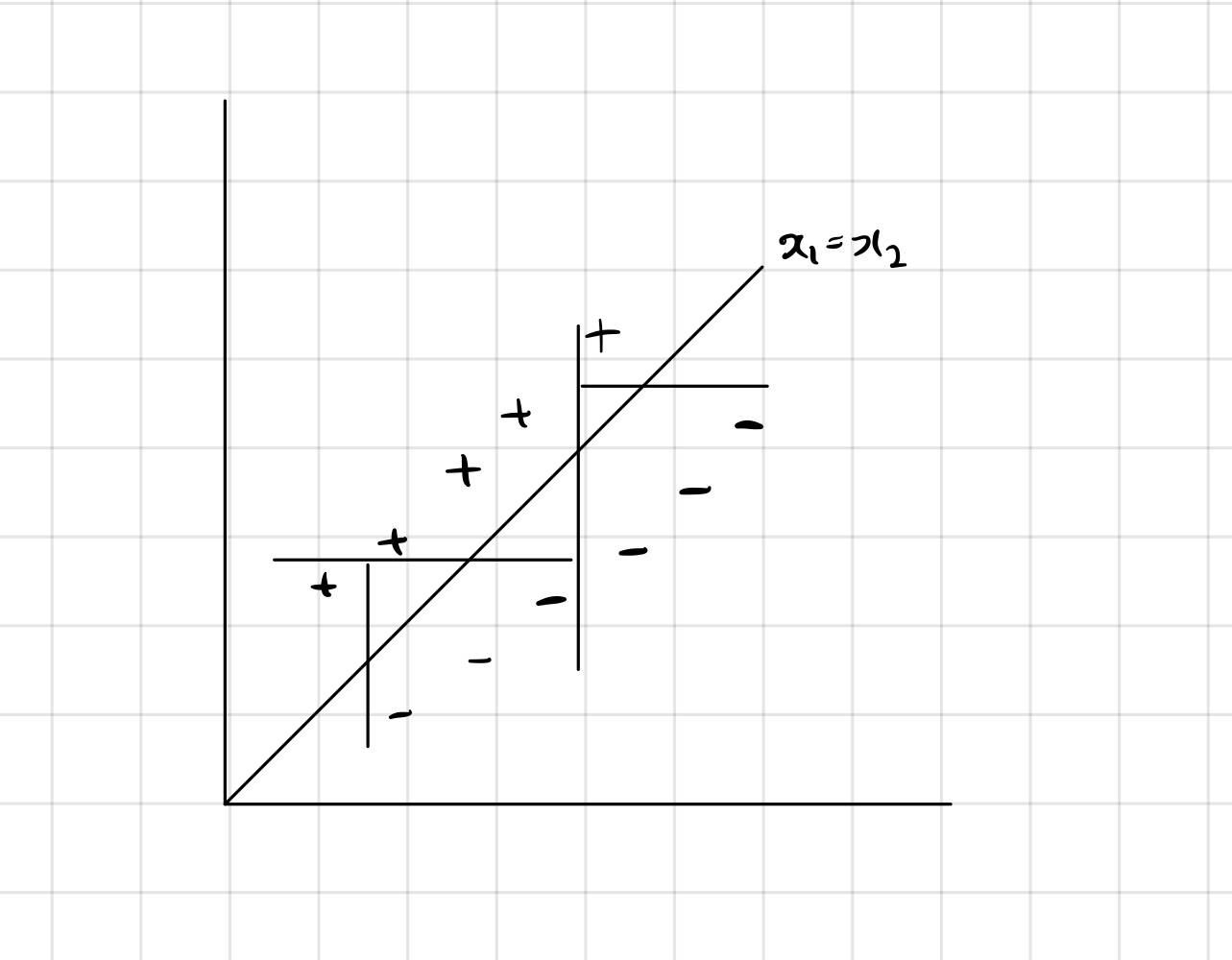
그런데 예시를 통해 살펴보면 이는 조금 문제가 있음을 알 수 있다.
이 두가지 경우에서 loss는 동일함을 알 수 있다.
이를 해결하기 위해 Cross-Entropy loss를 사용한다.
Cross-entropy
Miss classfication
에 따른 손실 그래프가 왼쪽 그림과 같다면, 의 위치를 이용해 평균점을 선택할 수 있다. 가 되는 점은 앞서 정한 평균점을 x 값으로 하는 점이 된다. 즉, 부모 지역의 loss 값보다 자식 지역들의 loss 평균값이 더 작아야함을 알 수 있다.
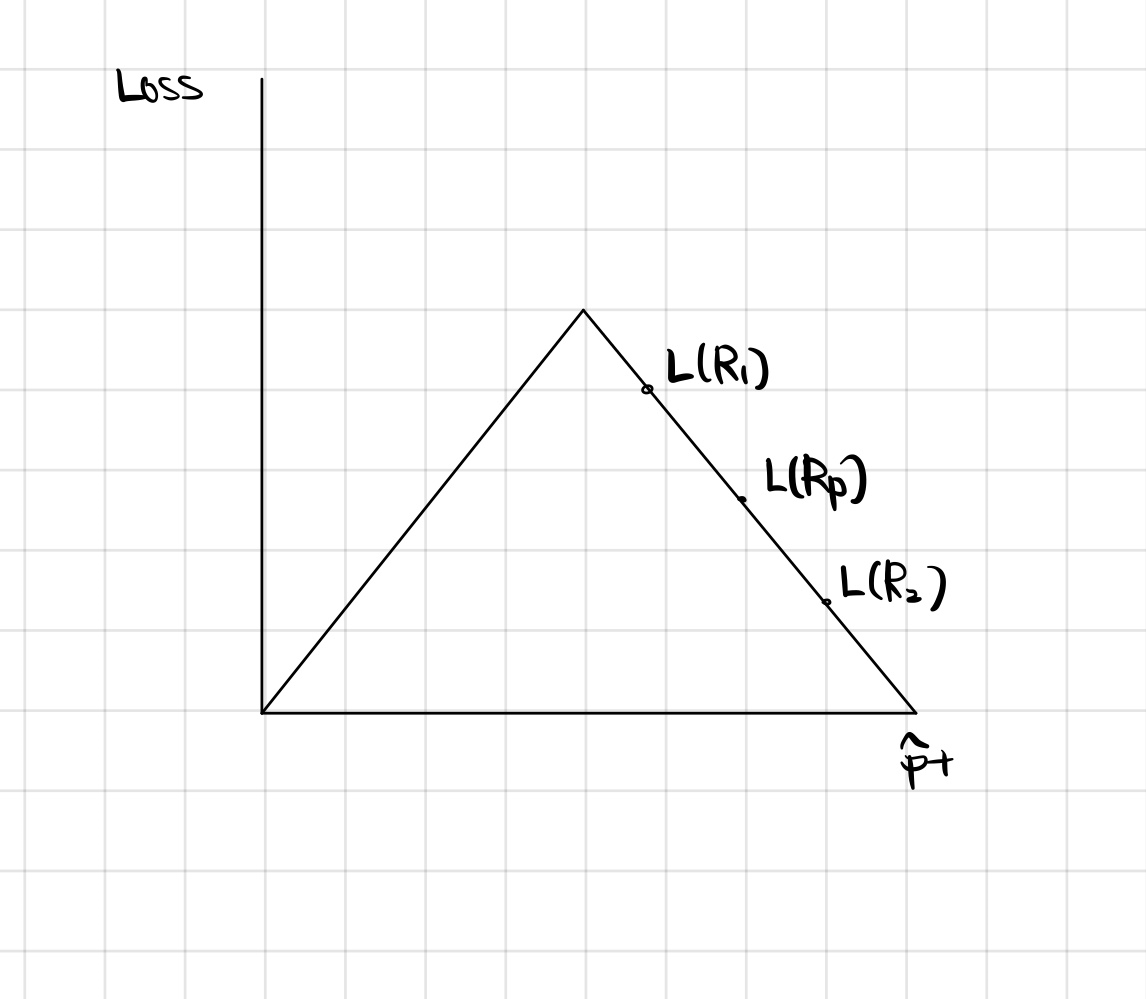
앞선 예로 확인이 해보면 다음과 같다.
의 의 , 의 이 된다. 의 손실 값이 과 의 평균과 정확하게 일치한다.
이 경우는 오른쪽 그림과 같이 와 loss 평균값이 같으므로 좋지 않다고 할 수 있고, 이런 경우 잘못 분류되었다고 생각한다. 즉, 의미없는 분류이다.
이 외에도 Gini라 불리는 다음과 같은 값도 자주 사용된다.
이 역시 Cross-entropy와 유사하게 그래프가 그려진다. (대부분 concave하게 그려진다.)
분류를 위한 결정트리 말고도 회귀를 위한 결정트리 역시 존재한다. 이를 Regression-trees라고 한다.
이번에는 적설량을 나타냈다. 앞서 했던 방식으로 분류를 하게되면 왼쪽과 같게 된다.
이제 어떤 지역 에 해당하는 예측값 을 수식으로 다음과 같이 나타낼 수 있다.
간단하게도, 지역에 있는 숫자들의 평균이다.
이제 다시 loss에 대해 생각해야 한다. MSE와 비슷하게 다음과 같이 정의된다.
이런 트리의 유용한 점 한 가지는 Categorical Vars를 사용할 수 있다는 점이다. 예를 들어 위도뿐 아니라 북반구, 남반구, 적도에 따른 분류도 가능하다. 하지만, n개의 카테고리가 있을 경우 분할이 되는 가능성은 총 이 된다.
트리 모델을 계속해서 훈련시키게 되면 최종적으로 각 데이터에 맞는 트리를 만들 게 된다. 이를 통해 트리모델은 분산이 상당히 높다는 것을 알 수 있고, 이는 Overfitting하다는 것을 말한다. 이를 방지하기 위해 정규화(Regularization)한다. 몇가지 경험적 방법은 다음과 같다.
- Min leaf size
- Max depth
- Max number of nodes
- Min decrease in loss
- Pruning ( misclassification with val set)
하지만, 4번의 경우 변수간의 상관관계가 있을때는 더 나은 질문을 먼저 하는 것이 loss를 줄이는데 좋다.
이제 이 모델의 Runtime을 알아보기 위해 트리모델이 n개의 예제와 f개의 features d만큼의 깊이를 가졌다고 가정한다.
이때, Test time은 depth의 크기인 O(d)가 된다. 만약, tree의 모양이 균형적이고 이진트리라면(한 쪽으로 치우져지지 않은 트리) 으로 생각 할 수 있다.
반면, Train time을 살펴보면 각 노드를 확인하는 것은 O(d)만큼 걸리게 된다. 또한, f개의 features가 있을 경우 각 노드에서 판단하는 시간은 O(f)이게 된다. 한 개의 노드를 처리하는 데 O(df) 이며 총 n개의 예제가 존재하므로, 최종적으로 O(nfd)로 빠른 모델이다.
이처럼 트리모델은 남에게 설명하기가 쉽고, 모델의 모형을 보고 해석하기가 쉽다. 또한, Categorical Vars에 유용하며 속도도 빠르다. 변수간의 연관성이 클 수록 좋은 예측을 한다.
Additive structure
하지만 단점 역시 존재한다.
오른쪽과 같이 데이터가 존재할 경우, 로직스틱 회귀를 통한 선형 결정경계를 구해서 아주 쉽게 분류가 가능하다.
하지만, 트리모델은 계속된 질문을 통해 영역을 나누게 되어 복잡한 트리가 만들어지게 된다.
이런 경우 속도도 당연히 저하되며, 분류역시 제대로 되지 않을 가능성도 생긴다.
또한, 트리모델은 높은 분산을 가지게 되어 Overfitting하기 쉽고 변수간의 관계성이 떨어질수록 예측성이 낮아진다.
Ensemble Methods
앙상블은 다양한 알고리즘들을 결합하여 사용하여 각각의 알고리즘들을 사용할 경우 나타나는 단점들을 보완한다. 트리모델에서의 단점도 앙상블을 통해 더 좋은 알고리즘이 된다.
우선 다음과 같은 가정을 한다.
- Take ’s which are random variables (RV)
- That are independent identically distributed (iid)
- ,
하지만, 이런 독립 가정은 실제로 x끼리 어느정도의 상관관계가 존재하기 때문에 종종 정확하지 않다. 이런 독립가정을 포기하고 다음을 생각한다. 이제 는 id가 되고 상관관계를 라 하면 다음 식이 성립한다.
가 0이라면, 는 iid 이다. 또한, 와 연관된 x가 증가할수록 당연하게도 분산이 커지며 n이 클수록 분산은 작아진다.
이를 위해서 Ensemble을 사용하는데, 다음과 같은 방법이 존재한다.
- Different algorithms
- Different training set
- Bagging (Random Forests)
- Boosting (Adaboost, xGboost)
Bagging-Bootstrap Aggregation
Bootstrap은 일반적으로 불확실성을 추정하기 위해 통계에서 사용된다. 모수의 분포를 추정하기 위해서, 표본을 복원 추출하고 각 표본에 대한 계산을 반복함으로서 신뢰구간을 결정하는 방법이다.
참인 모집단 P가 있을 때, training set S는 P에서 샘플링된다. 여기서 추출하여 각 set을 훈련시킬 수 있지만, 시간이 너무 많이 걸리게 된다. Bootstrap은 때문에 모집단 P가 training set S와 같다고 가정한다. 이제 S와 P가 동일하므로 Bootstrap sample Z를 S로부터 추출 할 수 있다.
이제 Bootstrap samples 을 추출하고 이를 이용해 모델 을 훈련한 후 각 결과의 평균을 구할 수 있다.
앞서 구했던 분산식을 가져와 생각해 적용해보면, Bootstraping은 기본적으로 훈련하고 있는 모델의 상관관계를 해제한다. 따라서 p의 값이 감소하게 되고, 더불어 원하는 만큼의 샘플을 추출할 수 있게 되므로 N ( 여기서는 M)의 수가 증가하여 전체적인 분산은 감소한다. 하지만, 편향은 랜덤하게 샘플링 한 이유로 조금씩 증가한다.
앞서 얘기한 Decision Tree는 높은 분산을 가지고 낮은 편향성을 지니기 때문에 Bagging과 잘 맞는다.
Random Forests
Random Forests는 앞서 말한 Bagging을 활용한 방법이다. 어떤 결과를 예측하기 위해서는 여러개의 features가 존재한다. 각 features를 기반으로 하는 하나의 트리모델을 만들게 되면 앞서 말했듯 overfitting이 일어나기 쉽다.
따라서, 이런 features들을 랜덤으로 일부만 추출하여 결정 트리를 만든다. 이를 반복하다보면, 여러개의 작은 결정트리가 만들어진다. 이 트리들의 결과를 통합하고 평균을 이용해 최종 예측값을 도출할 수 있다.
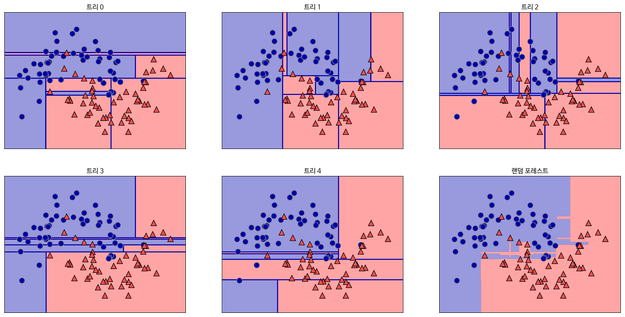
출처: 텐서 플로우 블로그
이런 방법은 트리를 하나만 사용할 때와 비교해 각 특성들의 상관관계인 p를 줄이거나 늘리게 된다. 즉, 각 feature들의 중요도를 값으로 나타내었을 때 하나의 결정 트리의 경우 영향력이 큰 feature만이 값을 정하는데 영향을 미치지만, Random Forests는 거의 모든 특성들이 값을 정하는 데 영향을 미친다.
Boosting
Boosting은 Bagging과 다르게 편향을 줄이는 방법이다.
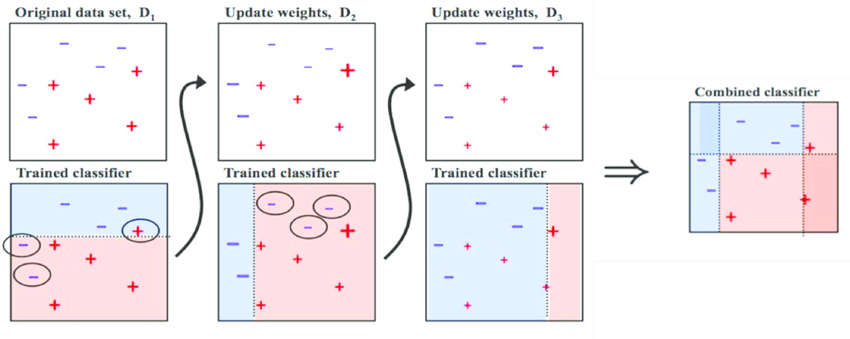
출처: Medium (Boosting and Bagging explained with examples)
다음 그림과 같이 첫 분류에서 잘못 분류된 +에 가중치를 준다. 그렇기 때문에 두번째 분류에서는 가중치를 고려해 가운데 그림과 같이 분류하게 된다. 다시 잘못 분류된 -에 가중치를 주고 +에 주었던 가중치는 조금 낮추는 방식으로 진행한다.
Adaboost에서 사용되는 가중치는 다음으로 알려져 있다.
앞서 말했듯 모델 들은 이전 훈련에서의 정해진 재설정된 가중치를 이용해 훈련을 반복한다.
Reference
https://tensorflow.blog/파이썬-머신러닝/2-3-6-결정-트리의-앙상블/
https://bkshin.tistory.com/entry/머신러닝-11-앙상블-학습-Ensemble-Learning-배깅Bagging과-부스팅Boosting
