Lecture 11
Deep learning
딥러닝에 대한 간략한 소개
- 딥러닝은 머신러닝의 하위분류 중 하나로써 특히 컴퓨터 비전, 자연어 처리, 음성인식 업계에서 사용되어 온 기술이다.
- 딥러닝이 발전하게 된 이유
- New computational power 딥러닝은 계산 비용이 많이 든다. 예를 들어 코드를 병렬화 하기 위한 기술과, 그래픽 처리장치를 위한 GPU를 사용하는 기술에서 많은 계산량이 필요하다.
- Big data 인터넷의 발전에 따라 사용할 수 있는 데이터가 증가했다. 따라서 사람들은 많은 양의 데이터에 쉽게 점근할 수 있게 되었다. 딥러닝의 경우 많은 양의 데이터가 있을수록 학습효과가 증가하기 때문에 딥러닝이 발전하게 되었다.
- New computational power 딥러닝은 계산 비용이 많이 든다. 예를 들어 코드를 병렬화 하기 위한 기술과, 그래픽 처리장치를 위한 GPU를 사용하는 기술에서 많은 계산량이 필요하다.
Logistic Regression
Goal1: Find soccer ball in images
- 모델 구축
사진을 통해 축구공을 찾는다고 생각을 해보자. 이진분류를 상용하여 축구공이 있으면 1, 축구공이 없으면 0을 출력해야 한다. 이때 이미지당 최대 하나의 축구공이 있다는 제약식이 존재한다.
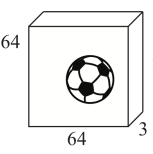
64 x 64의 이미지가 컬러 이미지라고 한다면 위의 그림과 같은 형태가 될 것이다. 위의 이미지를 벡터로 평면화 하면
그리고 위의 벡터는 다음과 같은 과정을 거치게 된다.
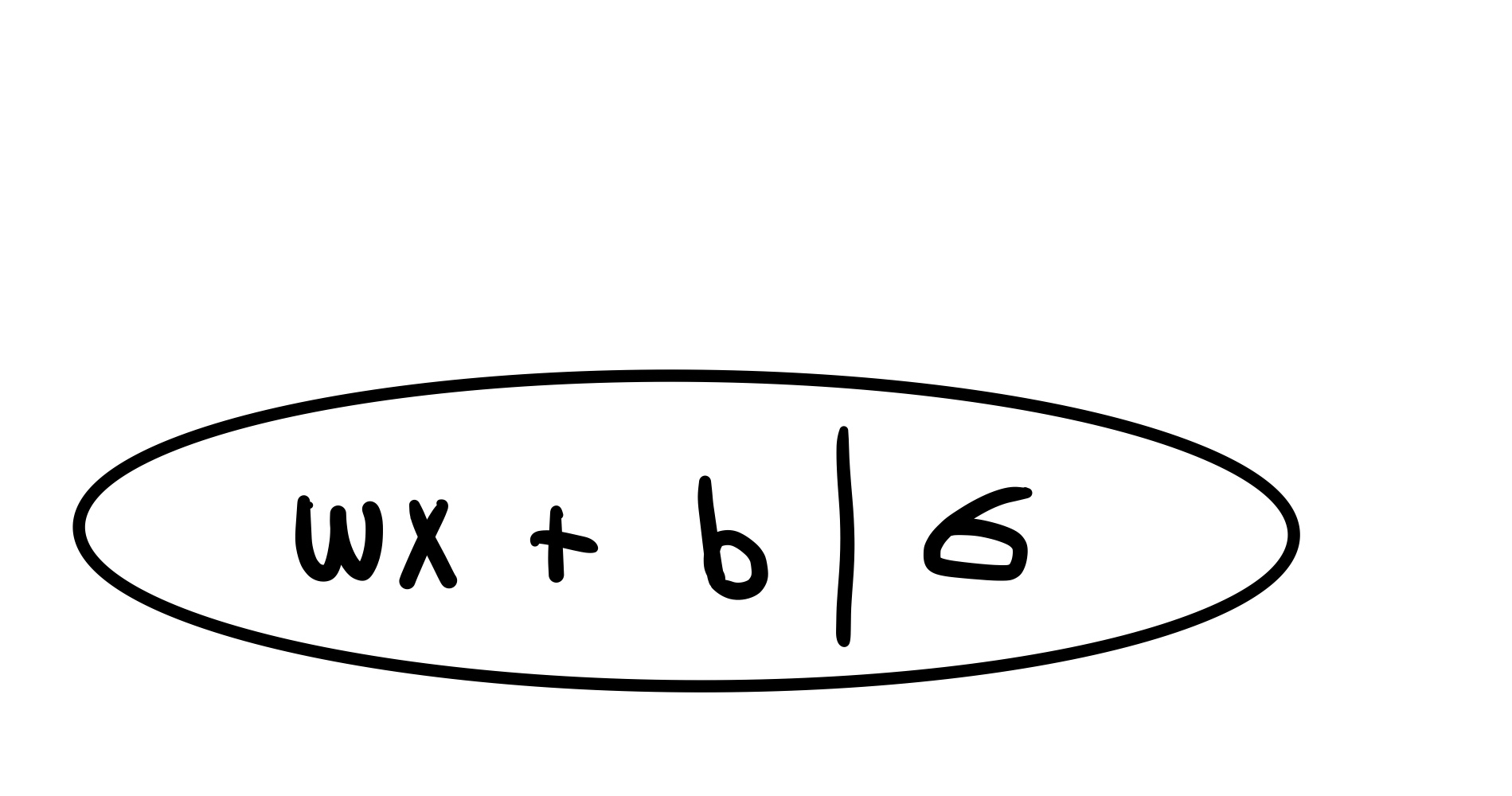
여기서 는 로지스틱 회귀에 사용되는 시그모이드 함수이다. 위의 과정을 거치면 우리는 다음의 결과값을 얻게 된다.
위의 식에서 는 (64x64x3=12288,1)의 벡터 형태이고, 가 (1,1)의 형태이길 원하기 때문에 는 (1,12288)형태를 띄는 벡터임을 알 수 있다.
- 모델 훈련 과정
앞서 얻은 모델을 통해 우리는 training을 해야한다. 훈련의 과정은 다음과 같다.
- Initialize ,
- Find the optimal ,
- Use to predict
2번(Find the optimal )의 과정을 더 자세히 살펴보자. 최적화된 매개변수를 찾는다는 것은 손실함수를 정의하는 것을 의미한다. 손실함수(비용함수)를 최소화 한다면 우리는 올바른 매개변수를 찾을 수 있다.이전에 배웠던 로지스틱 함수의 손실함수(비용함수)를 보면 다음과 같다.
손실함수를 최소화하는 매개변수를 찾기 위해서는 경사하강법을 사용해야 한다.
이렇게 손실함수를 경사항강법을 통해 최소하하는 매개변수를 찾아 모델을 훈련시킬 수 있다.
Goal 2: Find soccer ball/basketball/baseball in images
위에서 보았던 goal1과 다른점은 3가지 종류의 공을 분류하는 것이다. 만약 이러한 경우라면 네트워크를 어떤식으로 변경해야 할까?
- 모델 구축
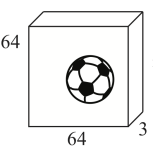
이미지를 벡터화 하는것 까지는 위의 goal1의 과정과 동일하다. 전체적인 과정을 한눈에 보면,
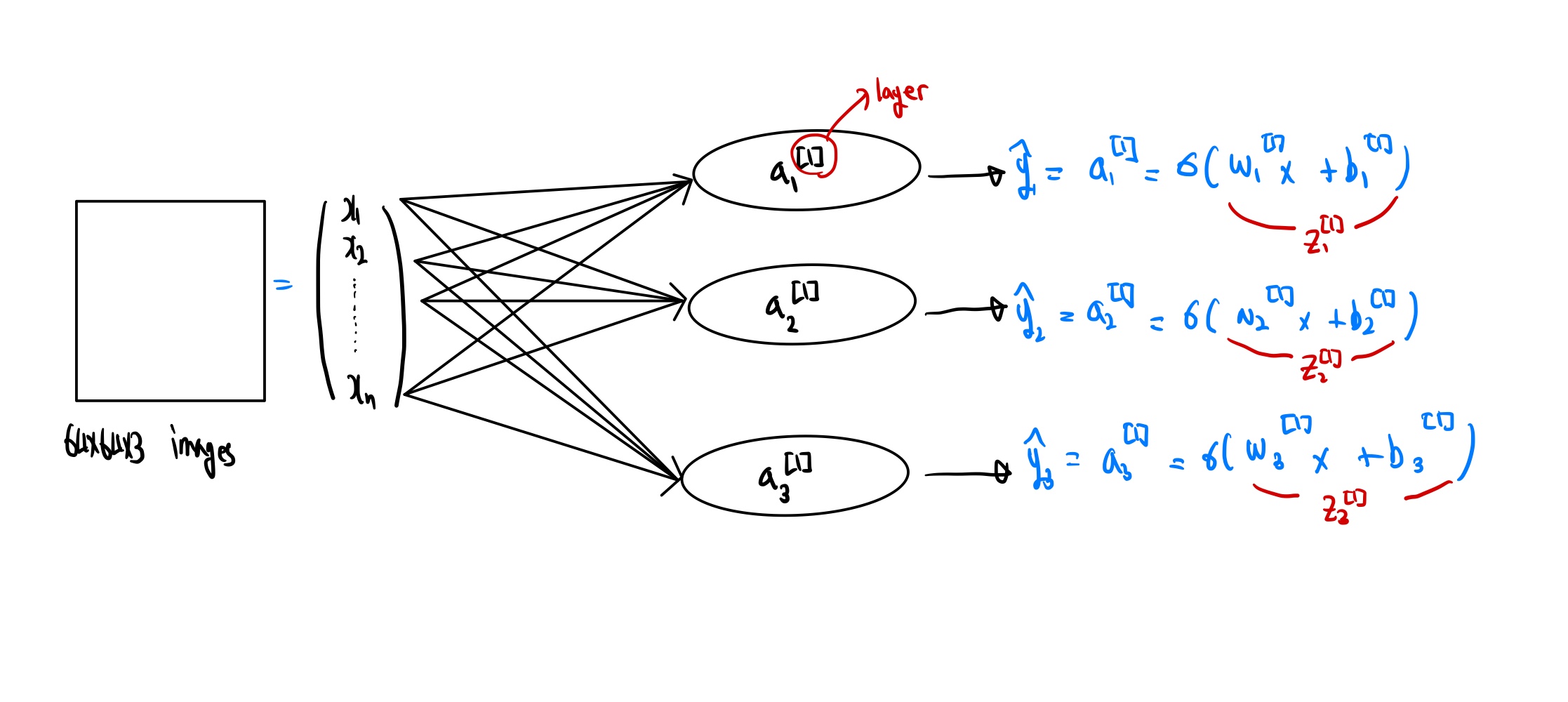
goal1에서는 데이터셋의 형태가 축구공인지 아닌지만 판별하기 때문에 이진분류의 형태이지만 이번 모델에서의 데이터셋은 3가지 다른형태의 공을 판별해야 하기 때문에 데이터의 형태는 다음과 같을 것이다.
첫번째 항의 1은 축구공의 판별을 나타내고, 두번째 항은 농구공, 세번째 항은 야구공을 판별한다고 가정한다면 위에서 살펴본 모델의 네트워크 은 각각 자연스럽게 축구공 ,농구공,야구공을 감지하게 된다. 만약 데이터셋의 레이블링을 다르게 한다면, 네트워크 도 각각 다른 값을 감지하게 된다.
만약 이미지 안에 축구공 뿐만 아니라 농구공도 같이 나오게 된다면 어떻게 될까? goal2 모델에서는
강력하게 작동 할 것이다. 그 이유는 3개의 네트워크가 서로 소통하지 않기 때문이다.
💡 만약 수많은 input 데이터중 하나의 야구공만 포함되어 있는 경우에는 야구공과 관련된 네트워크를 훈련하기에는 매우 힘들다. 따라서 이러한 문제를 해결하기 위해 제약식을 둔 새로운 모델을 살펴보자- 모델 훈련 과정
Goal1에서 활용한 모델 훈련 과정을 그대로 사용할 수 있을까? 정답은 그렇지 않다. 그 이유는 y의 결과 값이 0,1 두개 뿐이기 때문에 3개의 공을 판별하는 모델에서는 사용 할 수 없기 때문이다. 따라서 손실함수는 다음과 같아 진다.
Goal3: Unique ball in an images +constaint
💡 시작하기에 앞서 goal2 모델의 선형 부분을 $z_1^{[1]},z_2^{[1]}, z_3^{[1]}$로 부르기로 하자- 모델 구축
이전에 배웠던 softmax function의 개념을 사용하여 unique한 데이터에 대해 강력한 힘을 낼 수 있는 모델을 설정해 보자.
goal1, goal2 모델에서의 네트워크를 모두 로 대체해보자. 또한 특정 공식을 사용하여 다음과 같은 모델을 만들 수 있다.
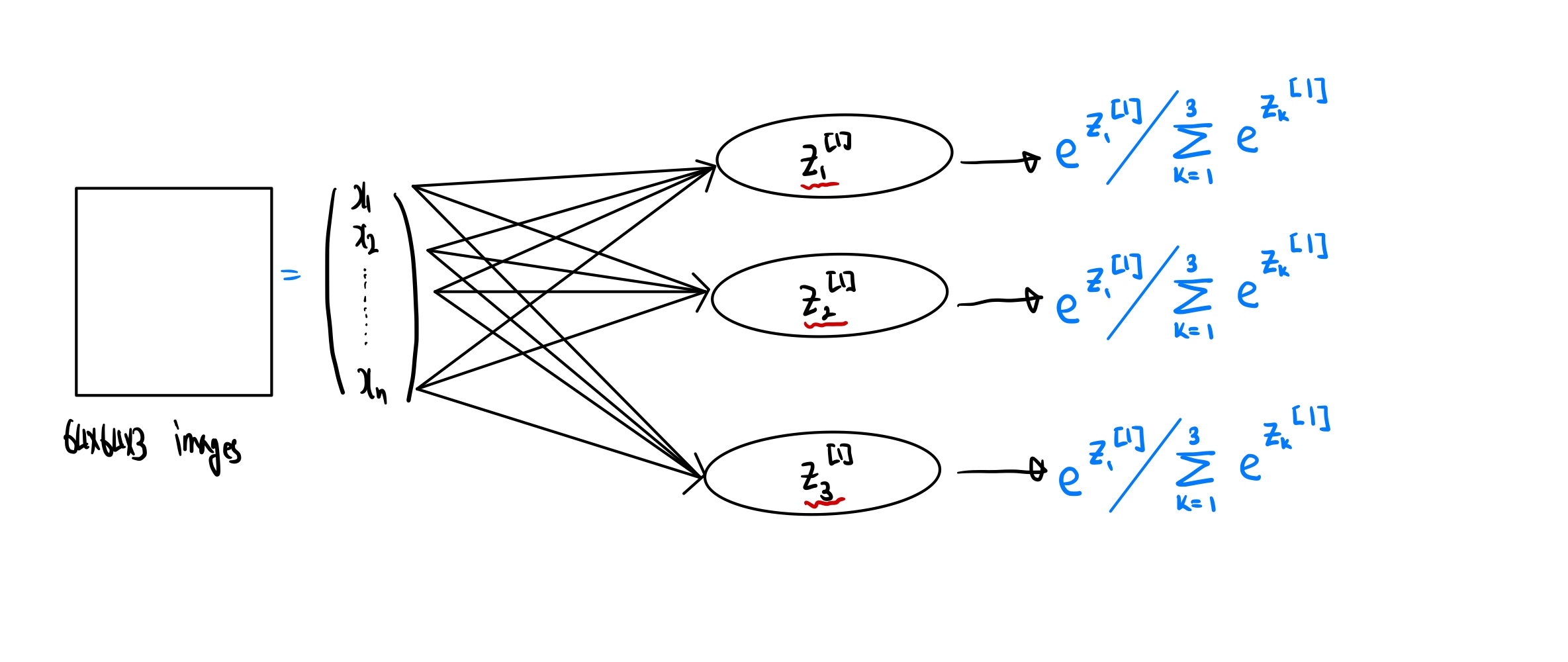
이렇듯 goal3의 모델의 독특한 점은 각각의 네트워크의 합이 1이 된다는 것이다. goal2 모델에서 처럼 결과값이 각각의 y에 대한 확률적 출력을 얻는 대신, goal3 모델은 모든 클래스에 대한 확률 분포를 얻는다. 에를 들어 다음 과 같은 결과값을 얻을 수있다.
위에서부터 차례대로 축구공, 농구공, 야구공의 확률을 나타낸다고 한다면, 모든 결과 값이 1이 되어야 하므로 축구공, 농구공이 거의 없다면 야구공이 있을 확률이 매우 높다는 것을 알 수 있다. 즉 세가지 확률은 서로 의존한다는 것을 알 수 있다.
이와 같은 모델을 softmax multi-class network 라고 부른다.
만약 만약 이미지 안에 축구공 뿐만 아니라 농구공도 같이 나오게 된다면 어떻게 될까? goal3의 모델은 작동하지 않을 것이다. 왜냐하면 2개의 이미지가 나타나게 되면 결과값의 합이 2가 되므로 합이 1인 softmax multi-class network 에서는 작동하지 않을 것이다.
- 모델 훈련 과정
만약 goal2에서와 같은 손실함수의 미분을 계산한다고 한다면, 이전보다 훨씬 복잡해지게 된다. 그이유는 손실함수에 직접적인 영향을 끼치는 이 식이 분모를 통해 각각의 네트워크와 연결되어 있기 때문이다.즉 w1이 w2,w3와 연결되어 있다. 따라서 sofrmax multi-class network에서는 새로운 손실함수의 정의가 필요하다.
위의 손심함수를 cross entropy loss 라고 한다.
Neural Network
Neural network의 과정을 살펴보자
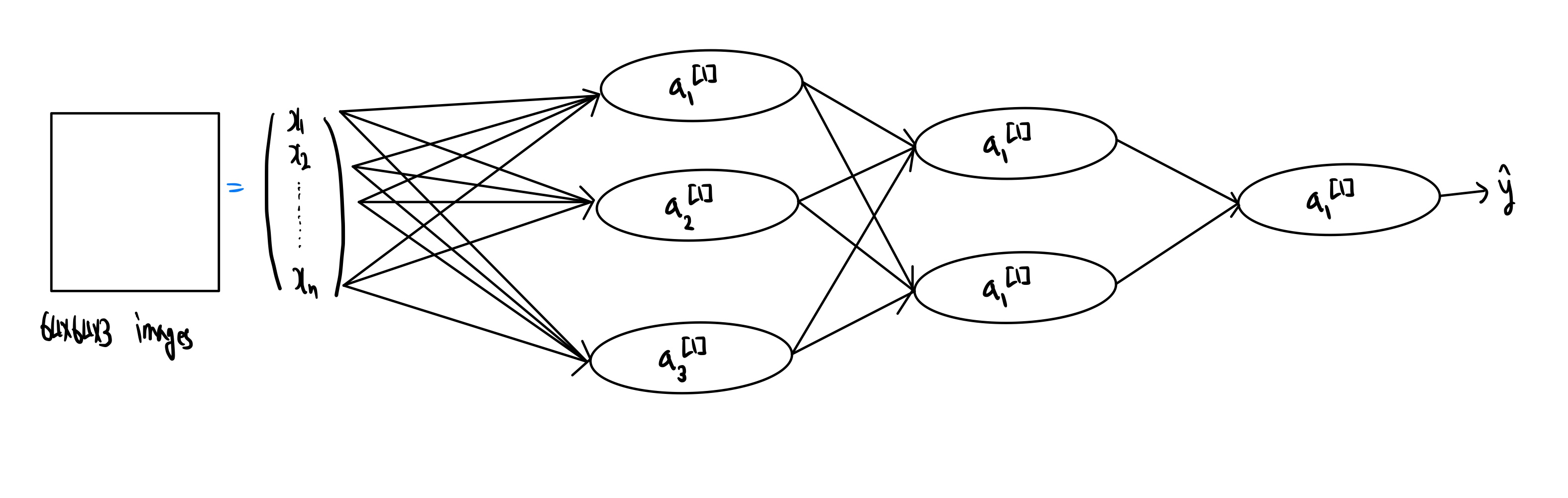
Why neural network is interstion?
예를 통해 알아보도록 하자. 축구공인지 아닌지 판별하는 문제를 다룬다고 가정하고 neural network를 통해 수많은 훈련과정을 거치게 된다면, 첫번째 레이어는 이미지의 가장자리를 이해하며 학습할 수 있다. 그리고 두번째 레이어 에서는 축구공의 특정 무늬를 파악할 수있고, 마지막 레이어 에선 축구공의 전체 모양을 학습할 수 있다. 그렇지만 우리는 2번재 레이어에서 데이터를 처리하는 방식을 이해할 수는 없다. 이때 2번째 레이러를 hidden layer라고도 한다.
또다른 예제를 통해 알아보자.
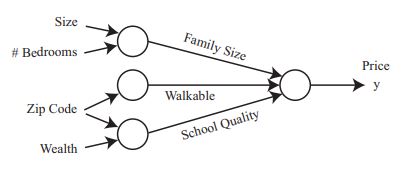
여태까지 많이 보아왔던 집 가격예측 예제 이다. input 데이터들은 집의 크기, 방의 개수, 우편번호, 재산 이다. 우리는 우편번호와 재산을 통해 학교의 quality를 결정 할 수 있다는 것을 알고 있다. 또한 우편번호가 걸을 만한 거리인지 알려주는 척도가 되기도 한다. 즉 네트워크가 인간의 사고방식 처럼 알아서 데이터들 간의 상호관계를 파악해 내는 것이다. 이렇듯 인간의 사고방식을 네트워크에 주입한 방식을 neural network 라고 한다.
Propagation equation
이번에는 neural network의 수학을 더 자세히 알아보고자 한다. 입력값으로 부터 출력값으로 전파하는 방정식을 작성해보자.
What happens for input batch of m examples?
만약 다음과 같은 m개의 예제를 한번에 제공했다면 어떻게 될까?
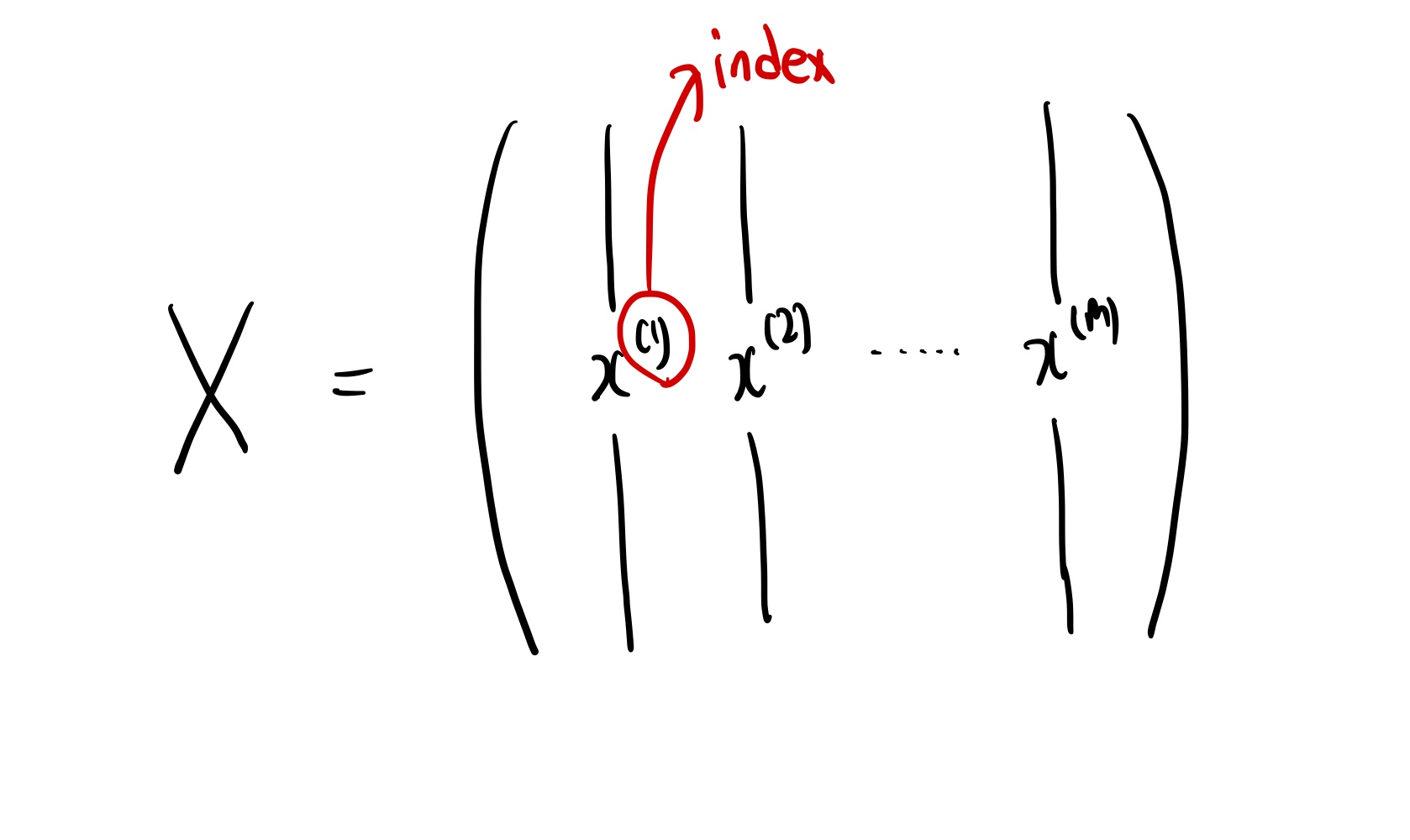
이러한 input이 들어오게 된다면 propagation equation은 어떤 형식으로 변형되는지 알아보자.
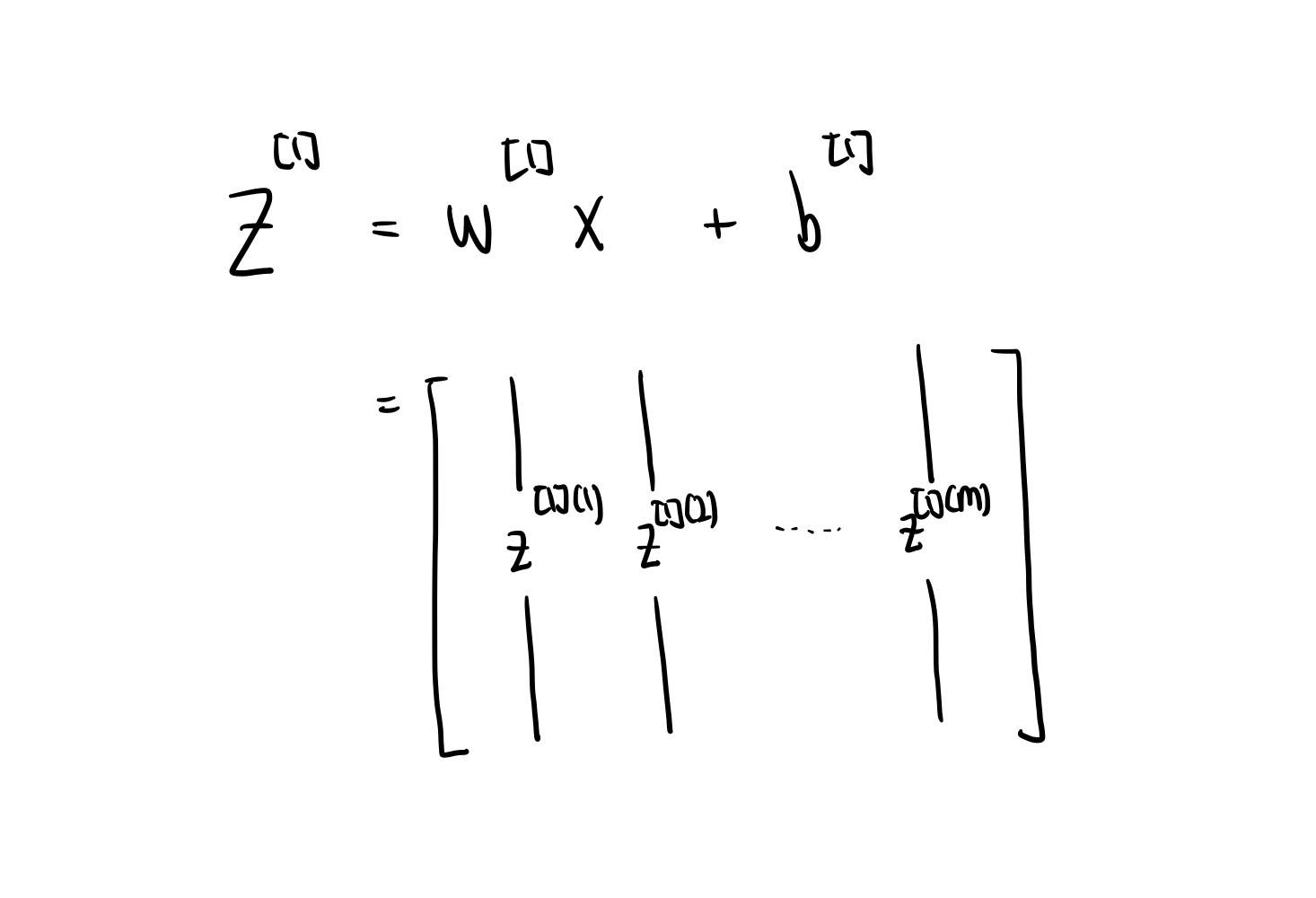
여기서 위의 방정식의 차원을 살펴보면, , , 이지만 차원이다. 여기서 문제가 발생한다. equation을 풀려면 3 X m 행렬과 3 X 1 행렬을 합산해야 한다는 것이다. 따라서 broadcasting 이라는 기술을 사용하여 방정식을 계산해야 한다.
💡 Broadcasting이란 매개변수의 수를 변경하지 않고, 위의 방정식을 풀수 있는 기술이다. 새로운 $\tilde{b^{[1]}}$ 을 정의하는 것이다. $\tilde{b^{[1]}}$ 는 ${b^{[1]}}$ 을 m번 반복한 행렬로 다음과 같다.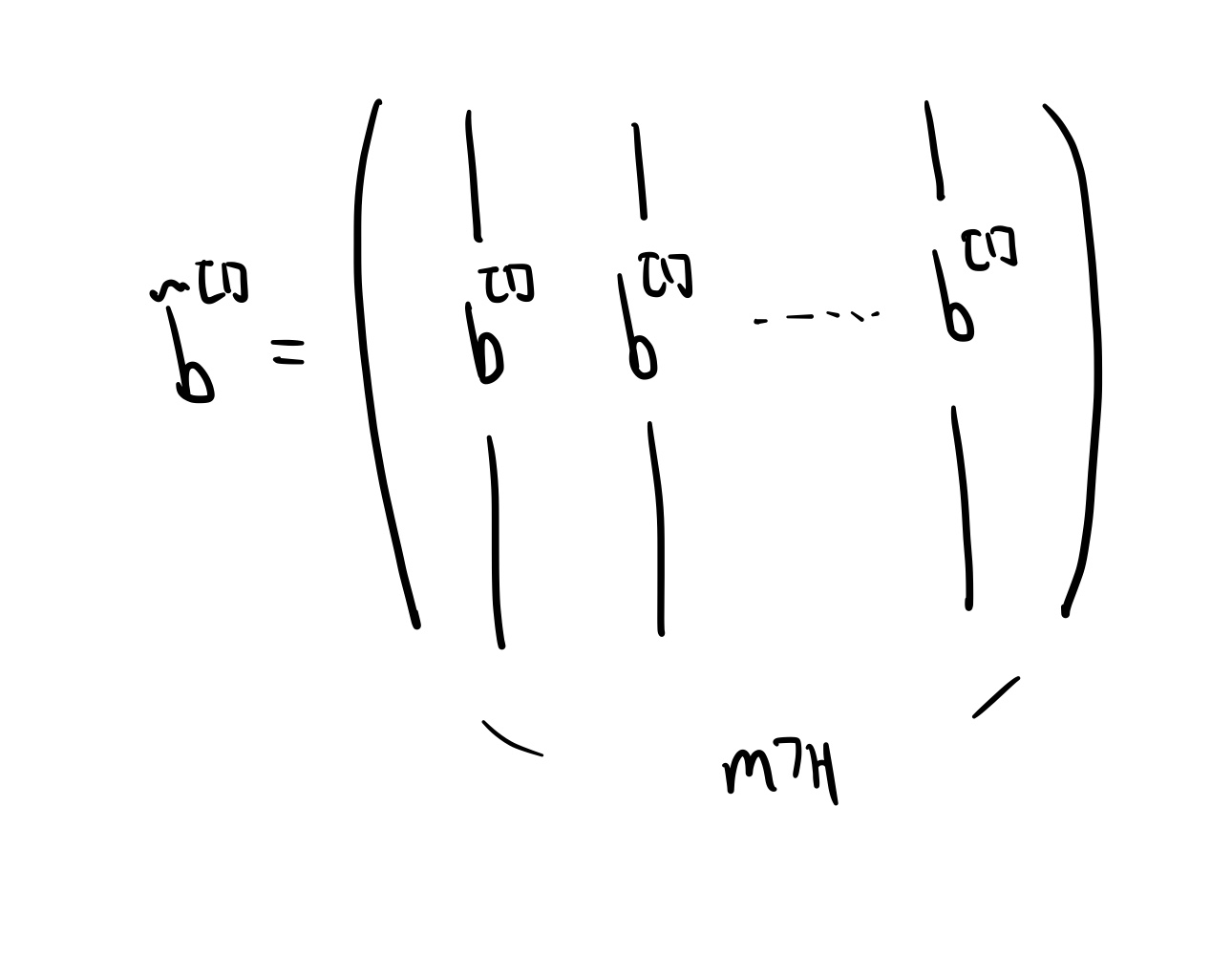
이렇듯 broadcasting 기술을 사용하면 propagation equation을 계산할 수 있게 된다.
