Lecture 9

Bias-Variance Trade off

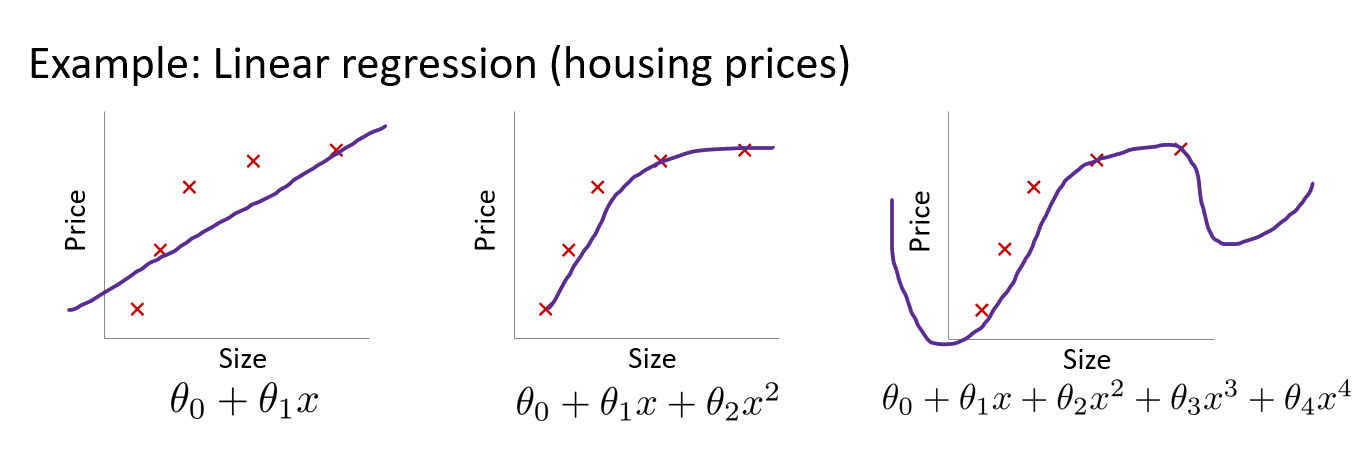
Assumptions

강의를 시작하기에 앞서 가정을 하고 시작을 하고자 한다.

• 데이터(x,y)는 분포를 가지고 (Data Distribution) 이 때, Train data 와 Test data 둘다 동일한 분포를 가진다.
• 모든 데이터 샘플들이 Independent samples이다. 또한 이 때의 샘플은 random variable이다.
• sample → learning algorithm(ESTIMATOR)→ hypothesis)의 과정을 지나면서 학습을 하는데, hypothesis 또한 random variable이다. hypothesis의 분포를 sample distribution이라고 한다.

$\theta^* or \ h^*$은 True parameter로 학습 알고리즘의 결과물이 되기를 바라는 정답 매개변수라고 한다.

또한 Random Variable이 아니며 그저 알 수 없는 상수이다.

$\hat{\theta}\ or\ \hat{h}$은 우리가 추정한 것이다.

Bias and Variance (View Point of Parameter)

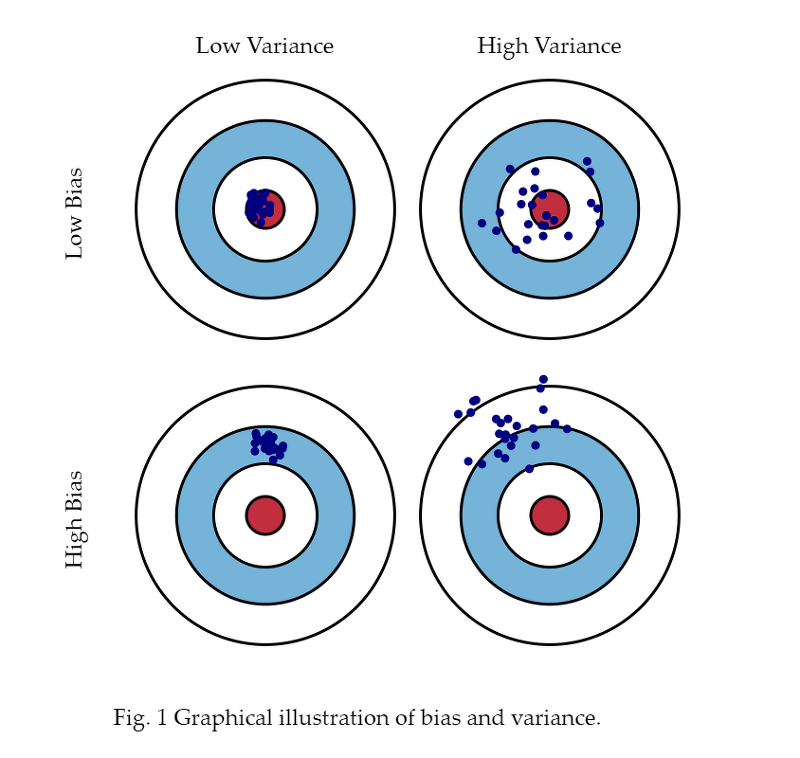
지난 강의에서 확인 해보았던 다음과 같은 그림은 Data 의 관점, 즉 (x,y)의 관점에서 확인 한 관점이다.

오늘 알아볼 Bias 와 variance는 매개변수의 관점이다.

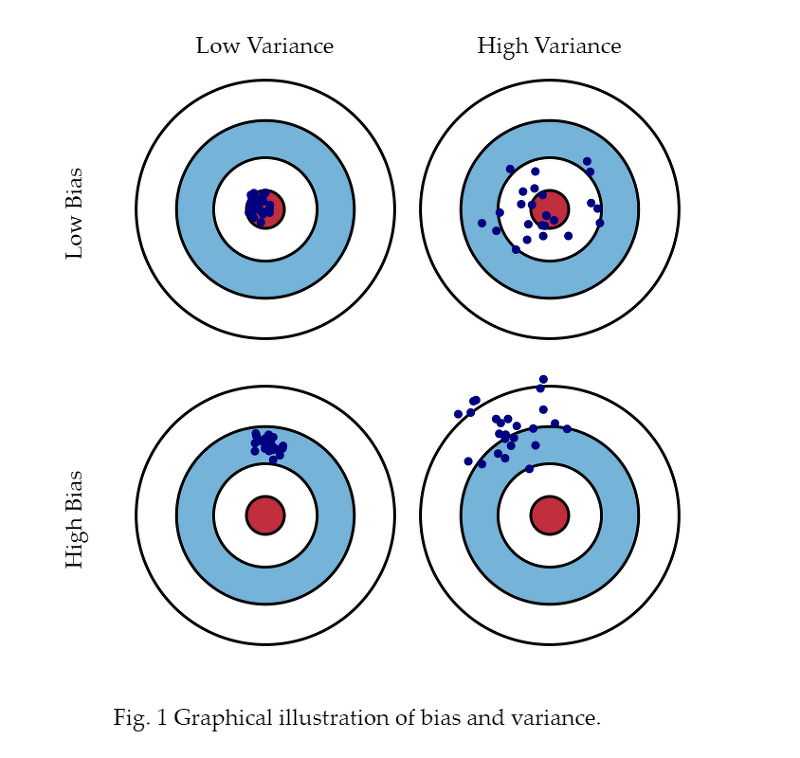
원판의 정중앙을 정답에 제일 가까운 매개변수라고 했을 때,

점들은 한 번 학습이 되었을 때, 구한 매개변수라고 할 수 있다.

Variance와 Bias는 독립적인 관계를 가지고 서로의 상관관계가 없다.

1. regularization과 같은 것들을 이용하면 분산이 줄어듭니다.

2. Data의 size가 늘어날 때마다, 점들의 간격이 줄어들기 때문에 매개변수의 분산이 줄어들거임!

   m→$\infin$ variance of $\theta$→0으로 간다.

3. Train data가 많아지면 추정값인 $\hat{\theta}\ = \theta^*$ 으로 진행이 된다. 결코 같아질 수는 없지만 가까운 값으로 진행이 된다.

📢 **용어 정리: statistical efficiency**: rate the variance drops to 0 as m tends to 0 **Consistent Model:** $m\rightarrow \infin ,$ $\hat{\theta} \ \rightarrow \ \theta^*$인 경우

Fighting Variance

1. 데이터의 양을 무한대까지 늘린다. 그러면 데이터의 분포가 더 집중되는 경향이 있다.
2. Regularization (Bias는 올라가지만 Variance는 낮아진다.)

Space of Hypothesis

---

h_star: H에서 g에 가까운 최고의 집합

h_hat: 데이터로부터 학습된 가설 및 파라미터

H: 무수히 많이 학습했을 때, h_hat들의 집합

g: 가설공간에서 제일 적합한 가설 (정답에 가까운)

Error in Hypothesis Space

---

이 때, 학습된 파라미터 $\hat{h}$은 정답 g와 차이, 즉 에러가 발생한다. 이 때 이 에러를 $\epsilon (h)$라고 한다.

Risk error/ Generalization error 라고 한다. 새로운 데이터를 misclassify 한 비율, 확률을 의미한다.

D라는 확률분포에서 계속 샘플링하여 long-term average 처럼 계속 계산합니다.

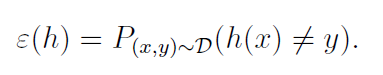
또한, 하나의 파라미터 샘플에 대한 에러를 $\hat\epsilon (h)$이라고 한다. Empirical Risk/ Training Error 라고 불린다. 모든 데이터 샘플에 대해 h(x)와 y기 다를 경우를 평균낸 것이다. 위의 Risk Error와의 차이점은 Training Error는 데이터의 개수가 있다는 점이다.

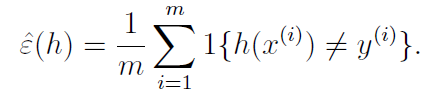
$\epsilon(g)$는 같은 x를 넣었을 때, 다른 y가 있는 예가 나오는 경우, 제거가 불가능 한 에러가 생긴다. Bayes Error/Irreducible Error라고 한다. 이론적으로 도달할 수 있는 최소의 classification error라고 한다.

$\epsilon(h^*)-\epsilon(g)$을 Approximation Error라고 한다.

$\epsilon(\hat{h})-\epsilon(h^*)$를 Estimation Error라고 한다.

고로 $\epsilon(g)$+$\epsilon(h^*)-\epsilon(g)$+$\epsilon(\hat{h})-\epsilon(h^*)$를 하게 되면 $\epsilon(\hat{h})$만 나온다.

$**\epsilon(\hat{h})$= Estimation Error + Approximation Error + Bayes Error 이다.**

Estimation Error 를 (Estimation Variance + Estimation Bias)로 바꾸고

Approximation Error를 (Approximation Bias)로 바꾸고

Bayes Error를 Noise로 바꾸면

이를 변환하면 Error = Variance + Bias + Noise 라고 한다.

Fighting High Bias

1. 가설들의 집합 H를 더 크게 만든다. 그러면 정답에 대하여 Bias는 줄고 Variance는 늘어나는 경향을 보인다.
2. 아예 다른 알고리즘을 사용하는 것

모델을 학습시킬 때, 우리의 목표는 bias와 variance가 모두 최소화되도록 하는 것이다.
그러나 최소화 시키는 것은 매우 힘들고 일반 적으로 힘들다.

📢 결국 **Bias Variance Trade off** 라는 것은

Bias를 줄이기 위해 가설들의 집합 H를 더 키우면 Variance가 늘어나는 경향을 보이고
Variance를 줄이기 위해 Regularization을 사용하면 가설의 집합인 H가 줄어들어 Variance는 줄지만 정답 g로 부터 멀어지기 때문에 Bias는 커진다.

Bias와 Variance는 같은 방향으로 가기 매우 힘들어서 절충해야 한다.

ERM (Empirical Risk Minimizer)

학습 알고리즘의 한 종류이다.

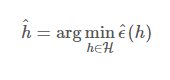
ERM은 분류에서의 training error를 최소화 시키려는 것이다.

Empirical Risk는 위에서 언급한 것 처럼

전체 데이터 샘플에 대한 loss function의 평균값이다.

고로 ERM은 Empirical Risk를 Minimize한다는 뜻으로 loss 의 평균을 최소화 시키는 방법이다.

Uniform Convergence

---

1. $**\epsilon(\hat{h})$ vs $\epsilon (h)$**
2. Generalization error of our learned hypothesis $\epsilon(\hat h)$ vs best possible generalization error $\epsilon(h^*)$

위의 두 가지를 비교하기 위해 여러가지 Tool들을 사용해보자.

1. Union Bound

$A_1, A_2, A_3, ... A_k$ 라는 사건이 있을 때 (독립적일 필요는 없다.) $P(A_1\bigcup A_2 \bigcup ...A_k) \le P(A_1)+P(A_2)+ ...+P(A_k)$ 이다.

1. Hoeffding’s Inequality

추정된 매개변수와 실제 매개변수가 margin을 벗어날 확률에 대한 부등식

$Z_1, Z_2, ....Z_m$은 독립적이고 파라미터 파이의 베르누이 분포에서 샘플링 된다.

이 때, $\hat\phi={1 \over m} \sum Z_i$라고 할 수 있고 $\gamma>0$이라고 가정하고 이를 margin이라고 한다.

probability of $[|\hat{\phi}-\phi|>\gamma] ]\le 2exp(-2\gamma^2m)$ 라고 할 수 있다.

여기서 샘플의 크기인 m이 점점 커지게 되변 부등식의 우변이 줄어들기 때문에

추정된 매개변수와 실제 매개변수가 가까워진다.

이를 약간 변형하면 아래와 같은 형태로 변형 할 수 있다.

이는 결국 샘플의 크기인 m이 점점 커지게 되면 generalization error ( 새로운 input 에 대한 error) 가 train error 와 가까워 짐을 의미한다.

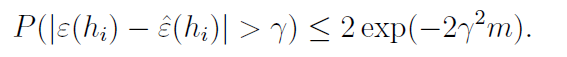
위의 식은 특정 hypothesis에 대한 식이 아니었기 때문에, 특정 hypothesis에 대해서는 성립하는지 보장할 수 없다. 그래서 우리는 모든 h에 대해 동시에 성립하도록 식을 바꾸고 싶다.

이 때, Union Bound를 사용해서 식을 변형할 수 있다.

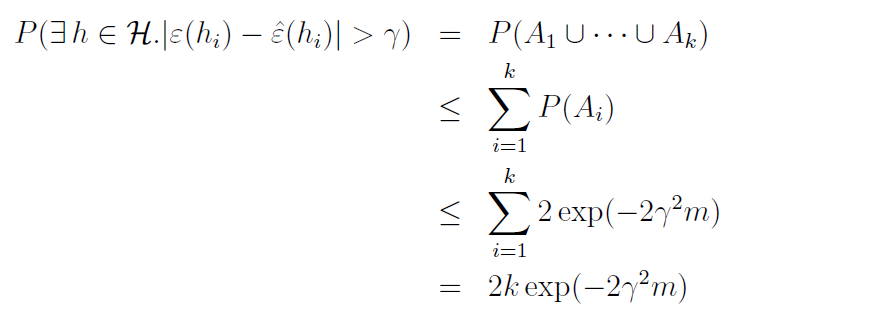
그 후에 부등식의 양쪽을 1에서 빼게 되면

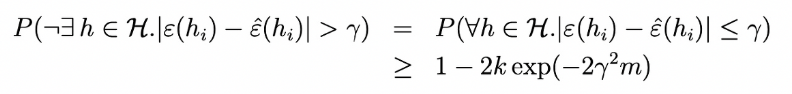
Sample complexity

이 때, $2kexp(-2\gamma^2m)$을 $\delta$, probability or error라고 하고 $\gamma$를 margin or error라고 하자.

Training error 와 generalization error의 차이가 margin 감마보다 작게 하기 위해 얼마나 많은 training dataset이 필요할까?

$**\delta \ge 2kexp(-2\gamma^2m)$이기 때문에 이를 풀게 되면 $m \ge {log{2k \over \delta} \over 2\gamma^2}$ 라고 할 수 있다.**

Generalization bound

위의 식을 다시 감마에 대해 풀게 되면 $\sqrt{{1 \over 2m} log{2k \over \delta}}=\gamma$이다.

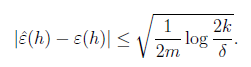
다음과 같은 식으로 바꿀 수 있다.

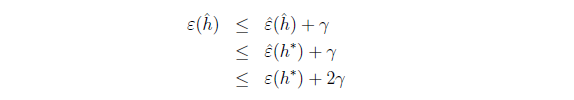
h_star은 hypothesis의 집합 H에서 가장 최고의 가설이기 때문에 위의 두번째 부등식이 성립한다.

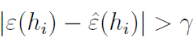
또한 다음의 식을 h_star에 대해 쓰게 되면 세번째 부등식 또한 성립한다.

이를 변형하면 최종적으로 아래와 같은 식으로 변형할 수 있다.

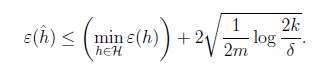
추정한 h에 대한 error는 가장 최고의 h에 대한 error+ 위의 값을 더한 값 보다는 작다.