Lecture 12
Deep learning
본 강의는 이전강의인 Lecture 11과 이어지는 내용이므로 참고 해주시길 바랍니다.
Backpropagation
훈련 과정 중 foward propagation이 진행되고 나면, 우리는 결과값 을 얻게 된다.
값을 얻으면 이제 비용함수를 계산한다.
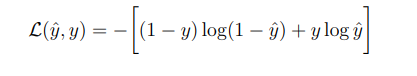
비용함수를 계산하고 난뒤, 경사하강법을 진행하여 각 매개변수들을 업데이트 한다.
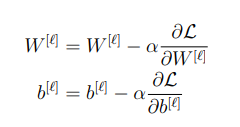
먼저 우리가 미분하고자 하는 식을 살펴보자
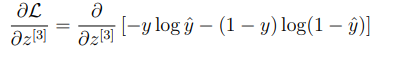
손실함수를 알고 있으므로 미분을 진행하게 되면,
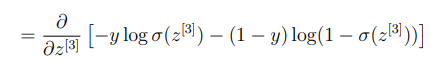
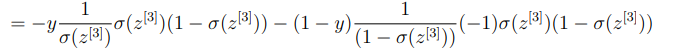
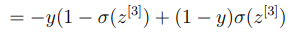
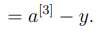
이제 손실함수를 로 편미분한 값을 구해보도록 하자.
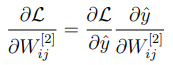
은 과 같으므로 다음과 같이 작성할 수 있다

이제 위해서 구했던 의 값을 활용하기 위해 다음과 같이 작성할 수 있다.
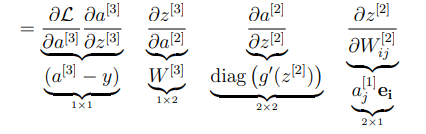
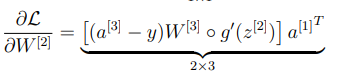
이렇게 로 편미분 할 때 구했던 값 를 이용하여 로 편미분 할 때 적용하는 것을 chain rule 이라고 한다.
Improving neural network
Use different activation function
앞서 보았던 예제에서는 activation function으로 sigmoid함수를 사용하였다. 그렇지만 우리가 neural network가 더 좋은 성능을 내기 위해서는 다른 activation funtion을 사용하여도 된다. 어떤 activation function들이 자주 사용되는지 알아보도록 하자.
- Sigmoid function
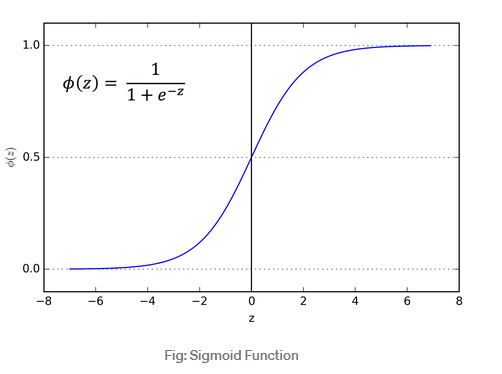
sigmoid function은 0부터1까지의 비선형적인 값을 갖고있는 그래프로써 neural network에서 activation function으로 많이 사용되고 있는 함수이다. 그러나 sigmoid function에는 단점이 있는데 바로 z의 값이 너무 크거나 너무 작다면, sigmoid fuction의 기울기가 0에 매우 근사한다는 점이다. 즉 backpropagation을 진행할 때, 경사하강법을 사용한다고 하더라도, 속도가 매우 느려진다는 단점이 있다.
- Tanh
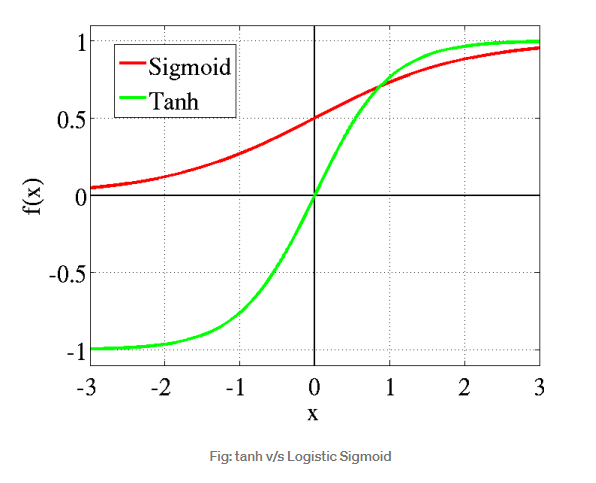
Tanh 함수의 장점은 sigmoid function과는 다르게 음의 값을 갖는다는 것이다. 강화학습처럼 음의 결과값이 필요한 경우가 있기에 강화학습에서 많이 사용된다. 하지만 sigmoid funciton과 마찬가지로 z의 값이 너무 커지거나 작아지게 된다면 매우 늦게 수렴한다는 단점이 있다.
- ReLU
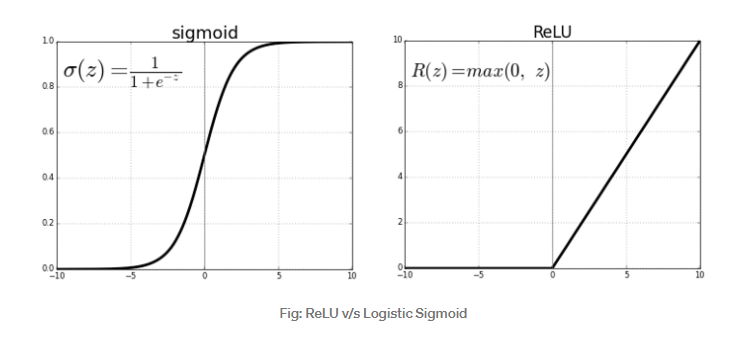
ReLU는 z의값이 음일때는 항상 0을 출력하고, z가 양수일때는 선형적인 값을 갖는 그래프이다. sigmoid function이나 tanh 함수와는 다르게 z의 값이 양의 무한대로 향하더라도, 기울기가 0이 되지 않는다는 장점이 있다. 하지만 z의 값이 음수라면, 항상 0을 출력한다는 단점이 있다.
💡 **Why do we need activation function?**만약 activation function이 선형적이라면, 즉 입력값과 출력값이 같다면 결과값이 항상 선형적이기 때문에 neural network가 다양하고 복잡한 데이터들을 처리하는데 도움이 되지 않기 때문이다.
Initialization method
초기값 설정은 매우 중요하다. 다음의 예제를 통해 그 이유를 알아보도록 하자.

만약 2개의 input값을 갖고 10개의 layer를 갖는 neural network가 있다고 가정해보자. 결과값을 살펴본다면 다음과 같은 결과가 나온다.
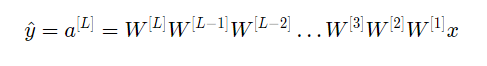
- case 1: exploding
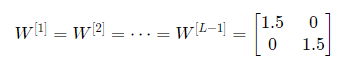
만약 1번 레이어부터 L-1 레이어까지 모두 같은 가중치를 위와같이 초기화 하였을 때 어떻게 되는지 살펴보자. 이렇게 된다면 의 값이 1.5씩 계속 곱해지는 값을 얻게되어 매우 커지게 된다.
- case 2: vanishing
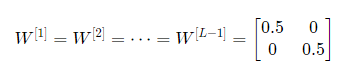
case 1과는 반대의 경우로, 결과값 가 0에 가까워지게 된다. 이렇듯 초기 가중치를 잘못 설정하게 된다면, neural network가 발산하거나 줄어드는 현상이 발생하게 된다.
그렇다면 초기값은 어떻게 설정해야 할까?
다음 두가지의 조건을 충족해야 한다.
- The mean of the activations should be zero
- The variance of the activations should stay the same across every layer
layer l 에 대해 더 자세히 알아보도록 하자.
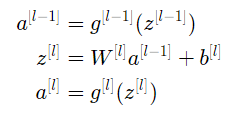
그리고 앞서 말했던 두가지 조건을 수식으로 표현하면,
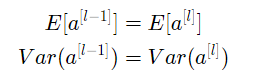
가장 유용하게 쓰이는 Xavier initialization에 대해 알아보자.
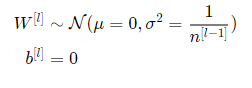
즉 layer l 의 모든 가중치들은 평균이 0이고 분산이 인 정규분포에서 랜덤하게 초기화 된다. 이렇게 하게된다면 exploding 하거나 vanishing 하지 않고 적절한 초기값을 사용할 수 있게 된다.
