Lecture 14

The k-means clustering algorithm

---

클러스터링은 비지도 학습 중 하나이다. 데이터 x가 주어질 때, 데이터를 그룹으로 묶는 알고리즘 이며 주로 Market Segmentaion에 사용된다.

![Untitled

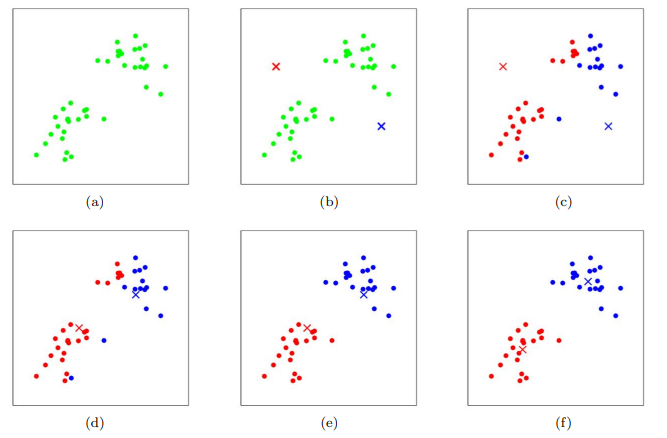
(a) 와 같은 레이블이 지정되지 않은 데이터가 주어지면, k-means는 우선 (b)와 같이 두 개의 십자가(클러스터 중심)로 표시된 점을 임의로 선택한다. 이후, 자신과 가까운 데이터를 구분한다. (c)와 같이 빨간색 십자가와 가까운 데이터들은 빨간색으로 칠해지며, 파란색 십자가 역시 마찬가지다. 이후, 각 데이터들의 평균점을 찾고 그 평균점으로 클러스터 중심을 옮기면 (d)와 같이 된다. 이를 반복하게 되면 최종적으로 (f)와 같은 2 그룹으로 나눌 수 있게 된다.

이를 수학적으로 표현하면 다음과 같다.

j = 1, … k 이며 c는 각 점, $\mu$는 클러스터 중심을 의미한다.

앞서 클러스터 중심을 임의로 설정한다하였지만, 실제로는 훈련 데이터에서 k개의 예제를 랜덤하게 추출한다. Cost function은 다음과 같이 쓸 수 있다.

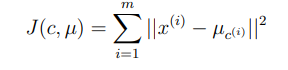
k를 선택하는 방법은 굉장히 모호하다. 사람마다 데이터를 4개의 그룹으로 나누거나 2개의 그룹으로 나눌 수 있기 때문이다. 그래서 주로 목적에 맞게 k를 선택하여 사용한다. (AIC나 BIC와 같은 공식도 존재한다.)

또한 이 알고리즘은, local minimum에 수렴이 될 때도 있다. 이를 방지하기 위해 알고리즘 자체를 여러번 실행 후 비용함수가 가장 작은 클러스터를 결정한다.

Density estimation

---

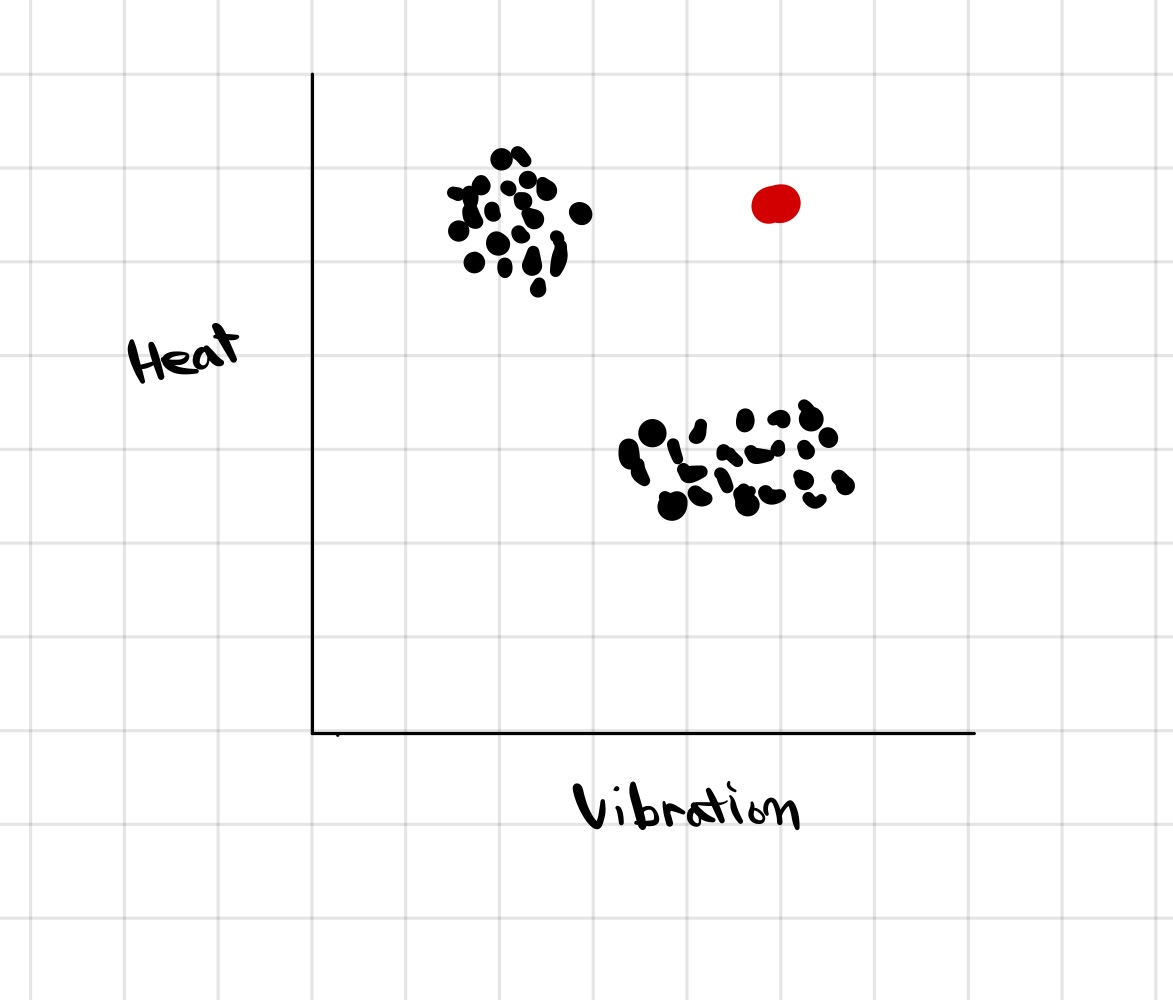
왼쪽 그림과 같은 비행기 엔진에 관한 데이터가 있다고 할 때 , 빨간색 데이터를 Anomaly Detection으로 탐지가 가능하다. 즉, 검은색 데이터들의 밀도를 확인하는 모델 P(x)를 만들었을 때, 밀도가 어떤 값보다 작다면 이상하다고 판단이 가능하다.

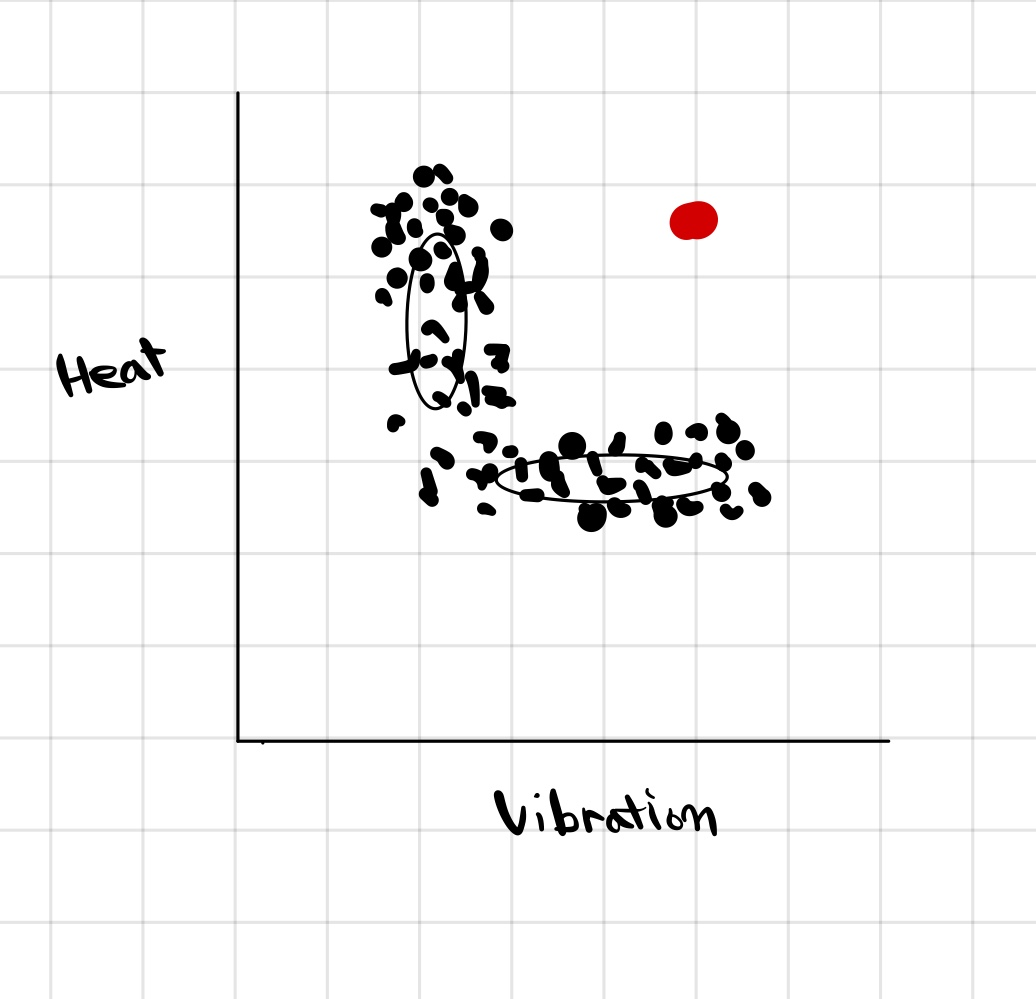
만약, 오른쪽 그림과 같이 데이터의 분포가 복잡하다면 그룹핑하기 어렵다. 이땐, 2개의 가우시안 분포를 이용하면 전체 데이터의 분포를 표현 할 수 있게 된다. 따라서, 데이터가 어떤 분포에서 추출될 확률이 높은지 알 수 있다.

Mixture of Gaussian model

---

들어가기 앞서 다음과 같은 가정이 필요하다.

1. Latent (숨겨져 있거나(hidden) 관측되지 않은(unobserved)) random variable z
2. $x^{(i)}, z^{(i)}$가 다음과 같은 joint distribution 을 가지고 있다.

만약, $z^{(i)}$를 알고 있다면 다음과 같은 MLE를 사용할 수 있다.

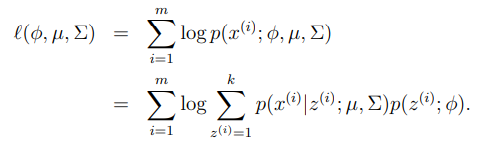
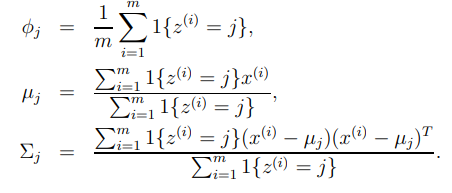
그러나, 실제로 $z^{(i)}$값을 알지 못하기 때문에, EM알고리즘을 사용한다.

EM( Expectation maximization)

---

이 알고리즘은 크게 2가지의 메인 스탭을 가지고 있다. 첫 번째로 E-step에서는 $z^{(i)}$의 값을 추측한다. 두 번째 M-step에서는 파라미터들을 이 추측을 가지고 새로 업데이트 한다.

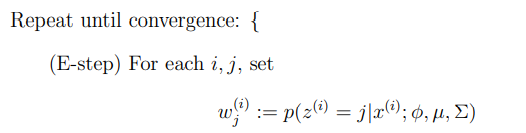
베이즈룰을 사용하면 다음과 같이 쓸 수 있다.

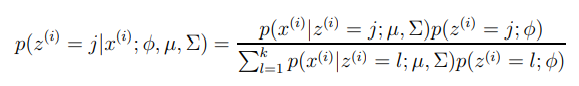
w^i = E[1{z^i = j }]

Jensen’s inequality

---

우선 f를 convex(볼록) function이라 하면, 이계 도함수는 0보다 크다. 또한, X를 random variable로 생각하면, f(EX) ≤ E[f(x)] 를 만족한다. 다음 그림을 보면 이해하기 쉽다.

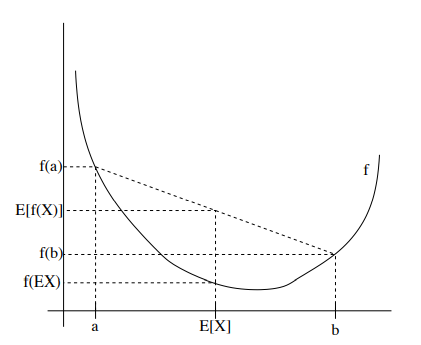
또한, 만약 f의 이계도함수가 0보다 크다는 것을 안다면 (f is strictly convex)

만약 concave 하다면, 앞서 말한 부등호의 방향은 모두 반대가 된다.

모델 $P(x,z ;\theta)$가 있고, $x = \{x^{(1)},....x^{(m)}\}$에 대해 관측했다면 로그 라이클리후드 $l(\theta)$는 다음과 같다.

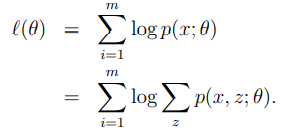
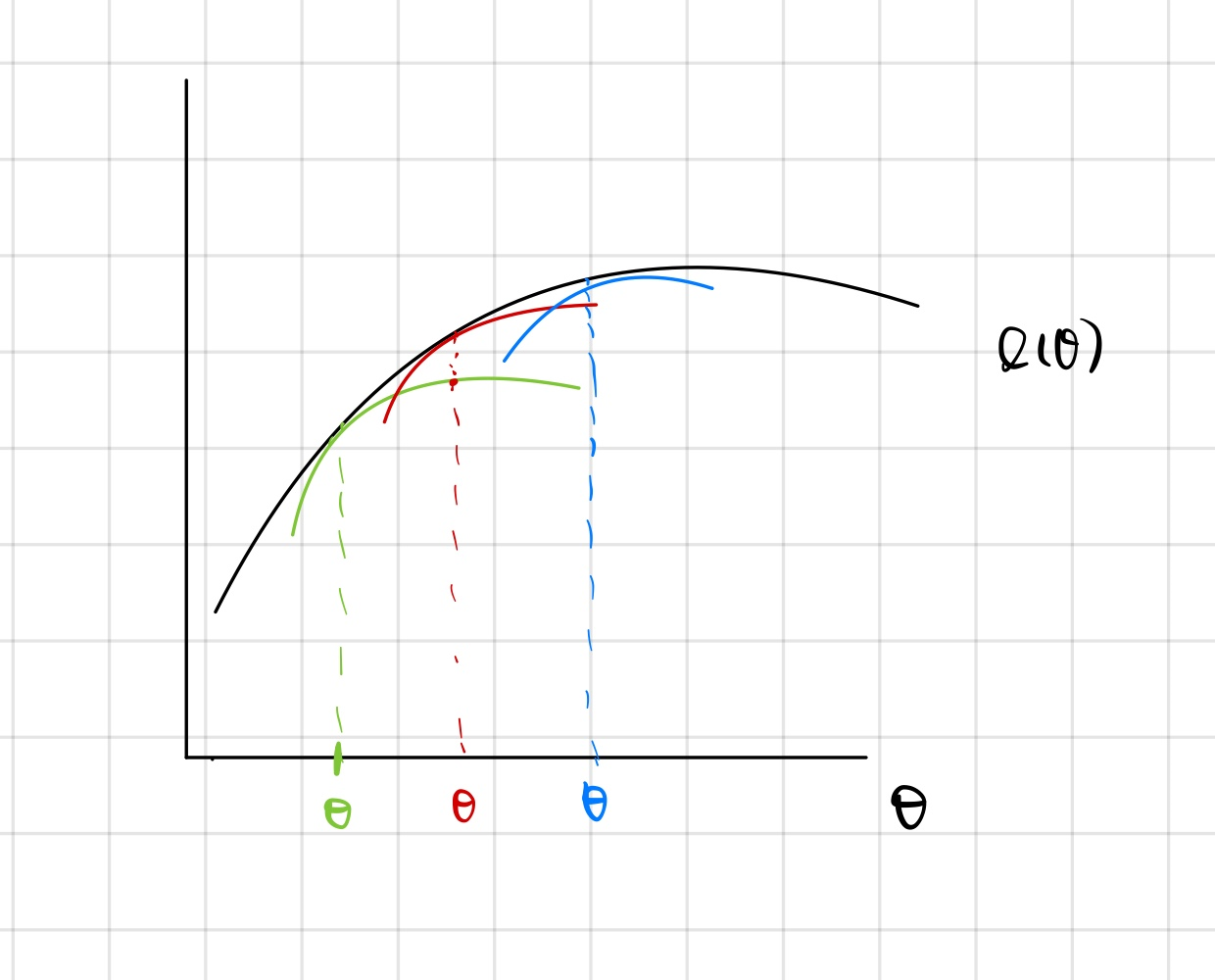
E-step에서는 우선 임의의 세타(녹색)점을 찾고, 곡선을 그린다.

이제, M-step에서는 녹색 선의 최대값을 찾는다. EM에서는 이제 theta값을 빨간색 theta로 옮긴다.

이를 반복하게 되면, 최종적으로 원하는 지점의 theta를 찾을 수 있다. 하지만, 이 뒤에 더 큰 theta값이 존재함에도, local optimum에 수렴하는 단점이 있다.

수학적으로 EM알고리즘에 대해 설명하면, $l(\theta)$는 다음과 같이 표현이 가능하다.

$Q_i(z)\text{ is a probablity distribution i.e }\Sigma_zQ_i(z)=1$ .

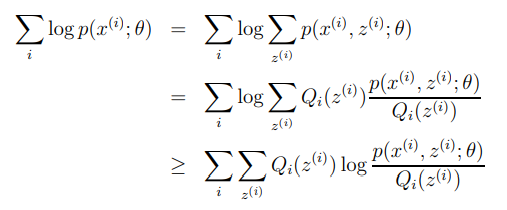
이제 앞선 식은 다시 다음과 같이 쓸 수 있다.

앞서 배운 Jensen’s inequality에 의해서 다음을 알 수 있다. (log 함수는 concave)

앞서 예시로 그린 녹색 곡선과 기존 곡선이 세타에서 같은 값을 가지는 것을 보장하기 위해서는 앞서 구한 식이 같아야 한다.

그러기 위해서는 다음과 같은 식을 만족해야 하고,

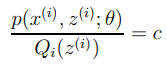
이는 다음 비례관계를 의미한다.

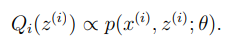
그 중 한가지 방법은,

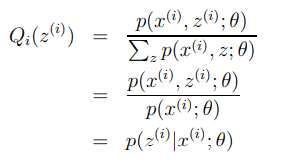
이를 요약하여 알고리즘으로 표현하면,