Lecture 15

들어가기에 앞서 Lecture5, Lecture 14, 가우시안 분포와 밀도, 기타 통계학 지식을 요합니다.

Mixtures of Gaussians

---

여러 개의 가우시안 분포들의 선형 결합으로 실제데이터의 분포를 근사하는 방법으로 아래와 같은 그림으로 표현할 수 있다.

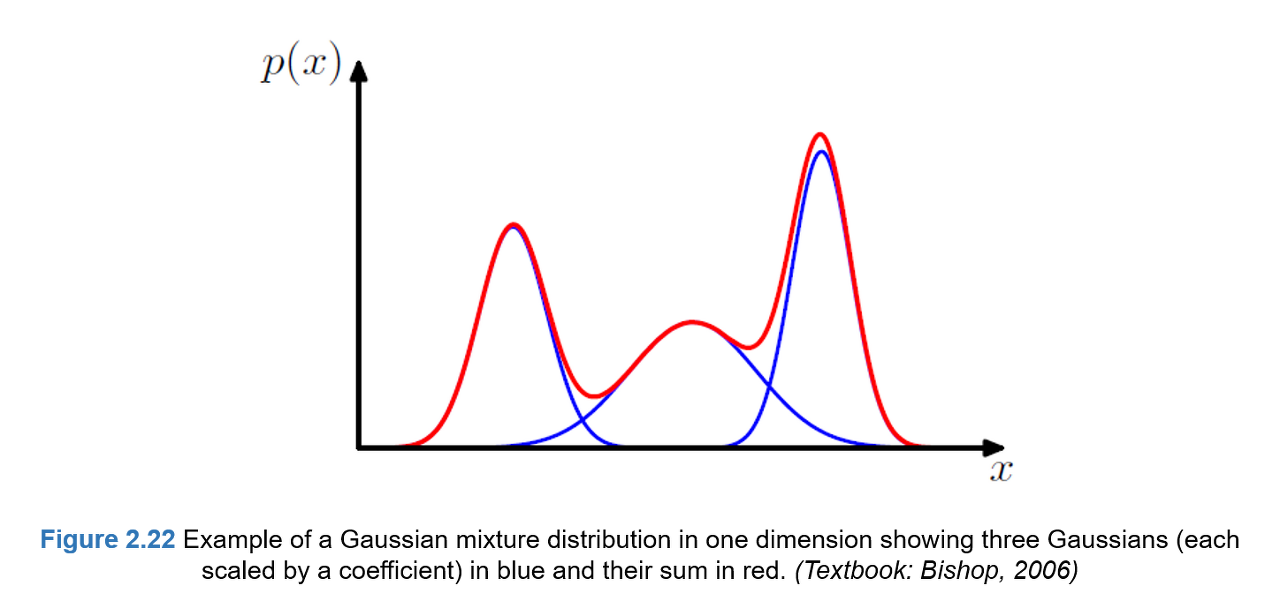
단일 가우시안 분포를 통해 데이터 분포를 표현하기엔 한계가 존재하고 복수의 혼합 분포를 사용해서 더 정확하게 표현할 수 있기 때문에 유용하게 사용되는 방법이다.

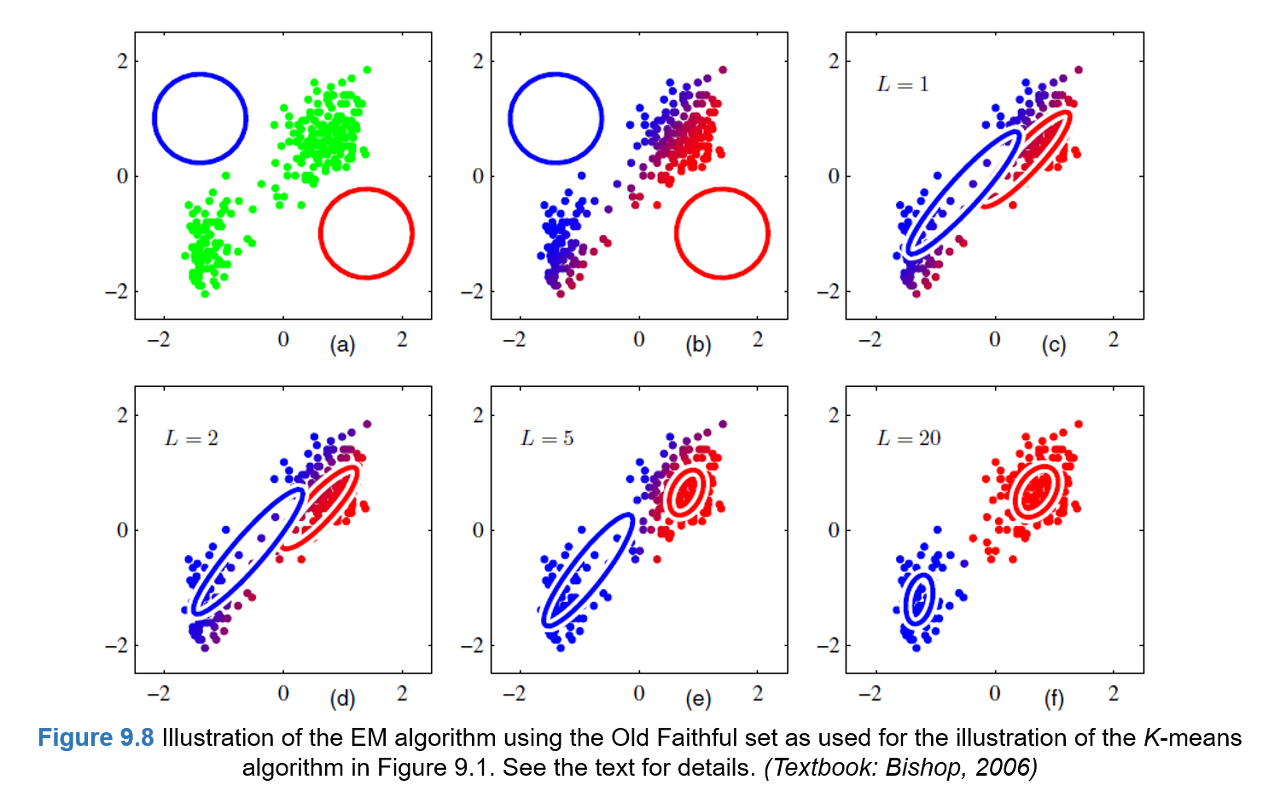
Mixtures of Gaussians에 대해서는 지난 Lecture14에 자세히 나와있기 때문에 계산과정을 약간 생략하도록 하자.

E-STEP

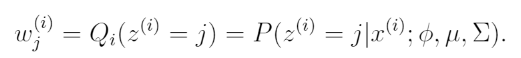
여기서 $Q_i(z^i=j)$는 z가 j의 값을 가질 때의 확률분포를 의미한다.

M-STEP

$\phi,\mu,\sum$을 최대화 시켜야 한다.

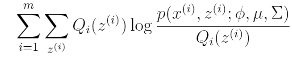
이 식을 Q(z=j) j=1부터 j=k까지 풀면

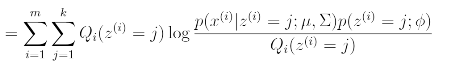
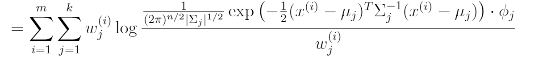
이 식을 $\mu$에 대하여 최대화 시키려고 한다. mu에 대해 미분을 취하면

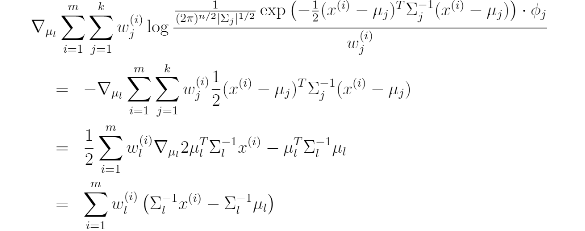
이러한 식이 나온다.

mu의 최대값을 찾고자 하므로 미분한 값을 0으로 설정하면

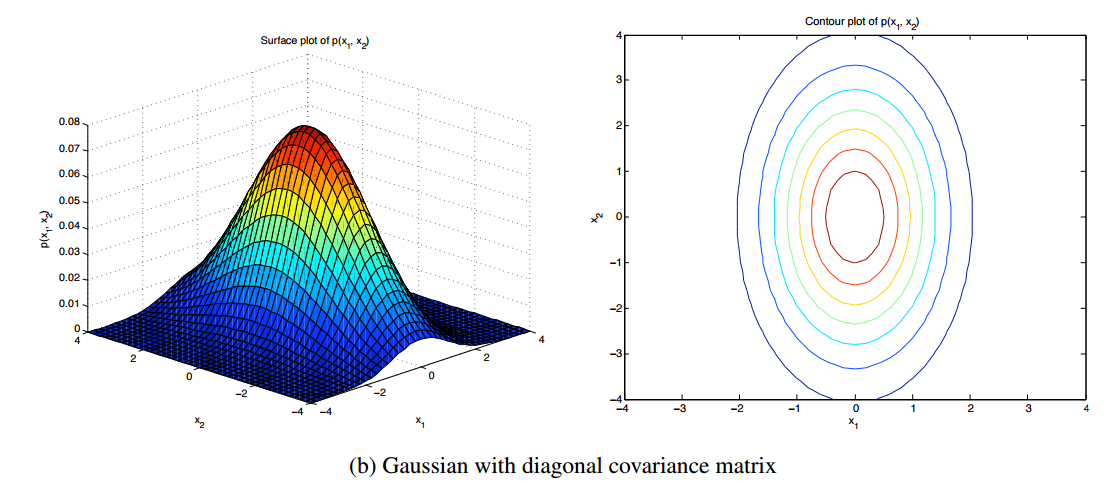
mu는 이러한 꼴로 정리된다.

이러한 방법을 $\mu$뿐만 아니라 다른 매개변수에 대해서도 할 수 있다.

Lecture 5

(Lecture 5의 GDA부분을 복습하면 더 도움이 될 것 같다.)

Properties

1. 혼합 가우시안 모델은 feature가 적고, 데이터 셋의 개수가 많을 때, 상대적으로 잘 동작한다.
2. feature의 수가 데이터 셋의 개수와 비슷하거나 데이터의 수가 feature의 수보다 훨씬 작을 때, 잘 작동하지 않는다.

위의 예를 single gaussian에서 확인해봅시다.

$x \sim N(\mu,\sum)$이라고 할 때,

Lecture 14와 Lecture 5에서 알아봤듯이, 그리고 M.L.E를 쓰게 되면

$\mu={1\over m}\sum x^i$라고 할 수 있다.

$\sum={1 \over m} \sum_{i=1}^{m}(x^i-\mu)(x^i-\mu)^T$라고 할 수 있다.

이 때, 데이터의 수가 feature의 수 보다 적으면 시그마가 singular/Non-invertible 행렬 (역행렬이 존재하지 않는 행렬)이 됩니다.

📢 공분산 행렬$\sum$이란?

공분산 행렬(covariance matrix)는 변수들 사이의 공분산을 행렬 형태로 나타낸 것이다.
data적으로 해석할 때, feature 사이의 상관관계를 확인할 수 있다.

한 확률 변수의 증감에 따른 다른 확률 변수의 증감의 경향에 대한 측도이다. 쉽게 말해 분산
이라는 개념을 확장하여 두 개의 확률 변수 의 흩어진 정도를 공분산이라고 하는 것이다.

Factor Analysis

---

위의 경우처럼 feature은 많고 data는 적은 경우, 가우시안 모델을 사용하면 좋은 성능이 나오지 않습니다. 이 때, factor analysis를 사용하곤 합니다.

예를 들어, 심리학 실험을 할 때, 100개의 질문 (100개의 feature가 있을 때), 30명을 대상으로 한다면, 가우시안 모델을 잘 작동하지 않습니다.

이 때의 대안 2가지에 대해 알아보도록 하겠습니다.

파라미터의 개수가 증가하게 되면 계산이 어려워지고 역행렬을 구하기 힘들기 때문에 다음과 같은 옵션을 제한하기도 합니다.

Option 1

공분산행렬 sigma를 대각행렬로 제한하자( 모든 feature가 상관관계가 없다는 전제)

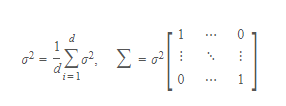
Option 2

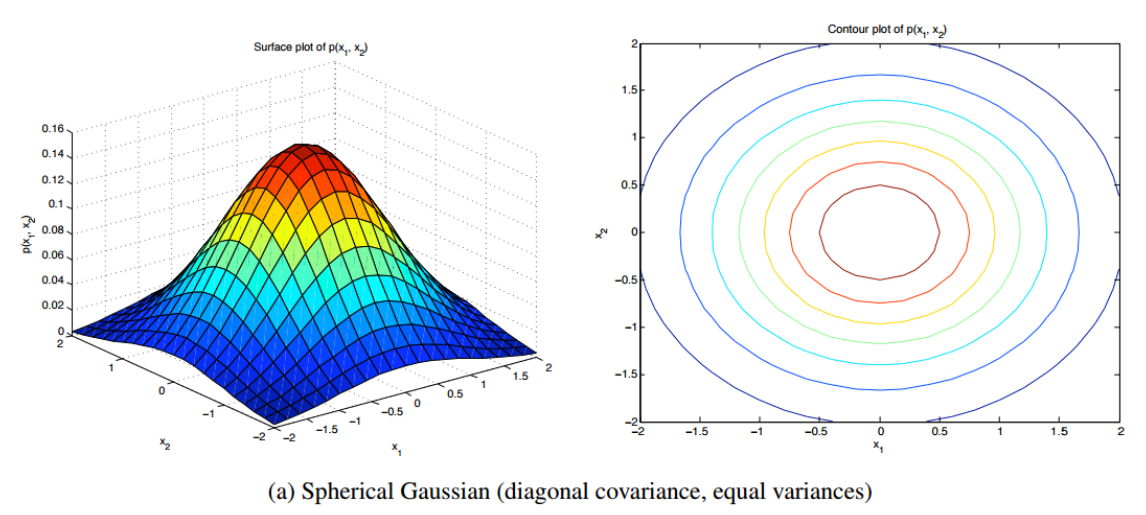
공분산행렬 sigma를 각 변수 별 분산을 전부 평균으로 놓고 단위행렬에다가 곱해서 분산으로 사용합니다. matrix가 대각선이 전부 같은 값을 가지기 때문에 항상 정규분포 모양이 원이 나오게 됩니다. 오른쪽 등고선 그래프를 보면 전부 원으로 나오는 것을 확인할 수 있습니다.

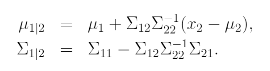
Factor analysis model

$P(x,z)=p(x|z)*p(z)$라고 하고 z는 hidden이다.

$z \sim N(0,I)$이고 $z \in R^d$

$x=\mu +\lambda z+\epsilon$이라고 가정한다. $\epsilon \sim N(0,\psi)$ 입실론은 noise이다.

위의 식을 기반으로 다시 식을 세우게 되면

$x|z \sim N(\mu +\lambda z,\psi)$라고 할 수 있다. ( 그 이유는 평균이 0에서 이동한 것이고, 입실론의 표준편차에 대해 정의를 하였기 때문이다.)

ex) 표본수 m=7, n=2, d=1이라고 할 때

$\lambda=\left[\begin{matrix} 2 \\ 1 \end{matrix}\right]$이고 $\mu=\left[\begin{matrix} 0 \\ 0 \end{matrix}\right]$라고 가정할 때,

$\lambda z + \mu \in R^2$ , $\psi=\left[\begin{matrix} 1 &0 \\ 0 &2 \end{matrix}\right]$라고 할 수 있다.

Multivariate Gaussian

다변량 가우시안에 대해 먼저 정의할 것이 있다.

$x=\left[\begin{matrix} x_1 \\ x_2 \end{matrix}\right]$라고 할 때, 윗부분 $x_1 \in R^r$, $x_2\in R^s$,$x\in R^{r+s}$라고 할 수 있다.

$x\sim N(\mu,\sum)$ 이라 할 때, $\mu=\left[\begin{matrix} \mu_1 \\ \mu_2 \end{matrix}\right]$이고 윗부분은 r의 부분 아랫부분은 s의 부분이라고 할 수 있다.

공분산 행렬$\sum=\left[\begin{matrix} \sum_{11} &\sum_{12} \\ \sum_{21} & \sum_{22} \end{matrix}\right]$라고 할 수 있다. 이 때, 11은 x_1과 x_1사의의 관계라고 할 수 있다.

Marginal Gaussian distributions

주변 확률 가우시안 분포란?

결합 확률 분포에서 한 쪽의 변수가 사라지거나 무시되는 것.

두 개의 변수에 대한 식을 새울 때, 한 쪽의 변수는 합산하여 사라지게 된다.

$p(x_1)=\int p(x_1,x_2)dx_2$라고 할 수 있다.

이룰 가우스 밀도 공식에 대입하게 되면?

$\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^-1(x-\mu))$ 여기서 x와 mu와 공분사 행렬을 위의 정의를 대입하면 된다.

위의 식을 정리하게 되면

$p(x_1) \sim N(\mu_1,\sum_{11})$라고 할 수 있다.

Conditional Gaussian distributions

가우시안 분포에서의 조건부 확률을 구하는 것이다.

$p(x_1|x_2)$에 대해 구해보자!

${p(x_1,x_2)}\over{p(x_2)}$에서 $x_1|x_2\sim N(\mu_{1|2},\sum_{1|2})$라고 할 수 있고

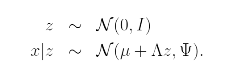
로 표현 할 수 있다.

(자세한 내용은 강의록을 참고하도록 하자)

지금까지 다변량 가우시안에서 조건부 확률과 주변확률에 대해 알아보았는데 이제부터 할 Factor analysis model에서 유용하게 쓸 예정이다.

Factor analysis model

1. (x,z)의 관계에 대해 알아보자

앞서 약간을 설명했기 때문에 다음과 같은 관계가 나옴을 알 수 있다.

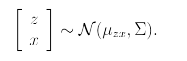
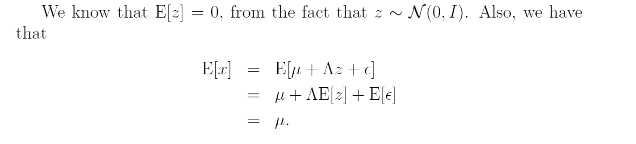
E[z]=0이기 때문에, E(x)=mu라고 할 수 있다.

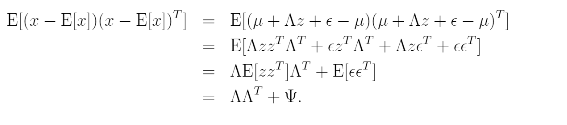
공분산 행렬을 구하기 위해서 z와 z, z와x, x와x의 공분산 행렬을 계산해야 한다.

$\sum_{zz}=Cov(z)=I$라고 할 수 있다.(왜냐하면 z가 평균 0에 분산 I를 따르기 때문에)

$\sum_{zx}=E(z-E[z])(x-E(x)^T]=E(z(\mu+\lambda z+\epsilon-\mu)^T]=E[zz^T]\lambda^T+E[z\epsilon^T]=\lambda^T$라고 할 수 있다.

마지막으로 $\sum_{xx}$는

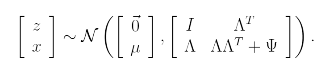
라고 할 수 있으므로 [z,x]는 아래의 분포를 따른다.

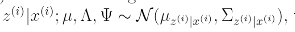
EM for factor analysis

E-step

goal: $Q_i(z^i)=p(z^i|x^i;\theta)$

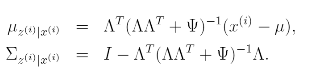
그리고 위의 조건부확률을 구하는 공식에 대입하게 되면 Conditional Gaussian distributions 아래와 같은 식이 세워진다.

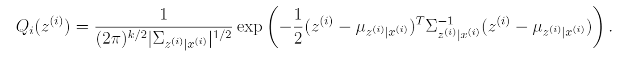
다시 Lecture 14에서 E-step을 할 때의 공식을 쓰면 아래와 같은 식이 나온다.

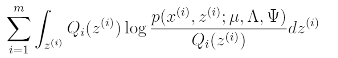
M-step

goal: maximize

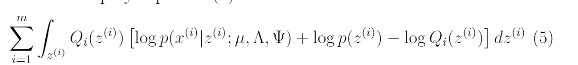
위의 식을 간단히 하면 아래의 식이 나온다.

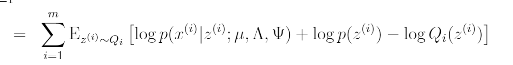
$E[z]=\int P(z)zdz$이기 때문에 아래의 식으로 간단히 할 수 있다.

maximize하는 것이 목표였기 때문에, 결국 미분을 취해야한다.

미분을 취하고 이를 0으로 보내는 작업이 굉장히 복잡하기 때문에 생략한다.