Lecture 16

Independent Components Analysis

---

ICA는 대표적으로 Cocktail party problem에 적용되는 모델이다. 파티에서는 여러 소리가 섞이기 마련인데, 이 소리들을 어떻게 분리하여 원래 소리를 추정할 수 있는지에 대한 알고리즘이다.

예를 들어 방에서 음악소리를 S1, 대화소리를 S2라고 하고 이를 두 개의 마이크로 녹음한 경우를 생각해볼 수 있다. 이때 마이크에 녹음된 신호를 각각 x1, x2라고 생각한다. 이때, 이 관계를 다음 식으로 표현 할 수 있다. A는 mixing matrix로 불리며, S를 Independet Component라 한다.

이때, $A^{-1} = W$를 찾을 수 있다면 손쉽게 source s를 얻어 낼 수 있다.

CLT(Central Limit Theorem, 중심극한정리)에 따르면, 독립적인 성분(s)이 많아질수록 이들의 선형 조합 x는 가우스 분포의 형태에 가까워 진다. 중심극한정리의 반대를 ICA로 생각하면 된다.

우선 데이터가 가우스 분포를 띄지 않는 것으로 가정하고 ICA 알고리즘을 생각해야한다. 첫 번째 단계로 ICA의 알고리즘을 개발하기 위해서는 S의 밀도가 무엇인지 알아야 한다. 이를 $p_s(s)$로 표현한다.

또한, 연속 환률 변수의 확률 밀도 함수는 CDF(Cumulative Distribution Function, 누적 분포 함수)을 통해 표현 된다. 이는 $F(s) = P(S\leq s)$ 과 같이 정의된다. $F'(s) = p_s(s)$ 가 성립한다.

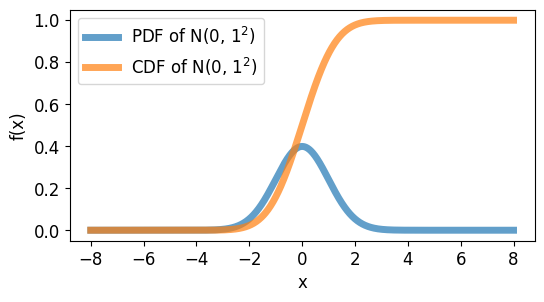
출처: https://codetorial.net/articles/normal_distribution.html

이제 어떤 F(s)를 정할 수 있고, 이를 미분하면 $p_s(s)$를 얻을 수 있다. 하지만, 기존 모델은 $x =As = W^{-1}s$ 가 되며, $s = Wx$ 이다. 매개변수에 대한 MLE를 찾기 위해서 $p_x(x) = p_s(Wx)$ 의 식을 생각해 볼 수 있지만, 이는 잘못된 식이다.

이를 알아보기 위해 $p_s(s) = 1\{0\leq s \leq 1 \}\space ( S \sim Uniform(0,1))$ 라고 가정한다. 또한, $x = 2 s$, (A=2 , w = 1/2 )라고 하면 다음과 같은 s와 x에 대한 확률밀도함수를 쉽게 생각 할 수 있고, $X\sim Uniform(0,2)$가 됨을 알 수 있다. 따라서, $p_x(x) = \frac{1}{2} *1\{0\leq x\leq 2\}$가 된다.

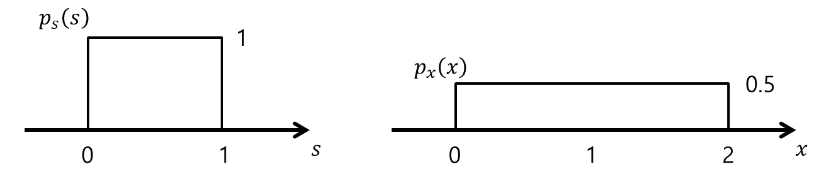
출처: https://angeloyeo.github.io/2020/07/14/ICA.html

즉, $p_x(x) = p_s(Wx)|W|$로 쓸 수 있다.

이제, $p_s(s)$를 가우스가 아닌 분포를 선택해주어야 한다. 앞서, $F(s) = P(S\leq s)$ 로 했고 이 모양을 가진 시그모이드 함수를 CDF로 설정한다면 ICA가 잘 작동할 것이다. (이중지수분포, 라플라스분포 역시 잘 작동한다.)

마지막 단계로, ICA에서 가장 중요한 가정 중 하나는 다음 식이다.

앞서 얻은 식을 이용하면,

매개변수를 추정하기위해 MLE를 사용하면,

Stochastic Gradient ascent :

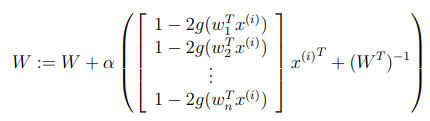
다만, 아직까지 비선형 버전에 대해 명확하게 말할 수 있는 알고리즘은 없다고 알려져있다.

Reinforcement Learning

---

소위 말하는 강화학습은 쉽게 말해서 설계자가 자동으로 나는 헬리콥터를 모델링 할 때 제대로 난다면 좋은 보상을, 날지 못하면 좋지 못한 보상을 주는 것이다. 따라서, 모델의 설계자의 목표는 헬리콥터에 대한 보상 함수를 만드는 것이라 말할 수 있다. 대표적으로 체스는 강화학습의 좋은 예중 하나이다.

강화학습을 어렵게 만드는 것 중 하나는 Credit assingment problem 이다. 예로 체스게임에서 50번을 이동해서 졌다고 가정하면 -1의 보상을 얻게 된다. 그러나, 실제로 몇 번째의 이동에서 컴퓨터가 실수를 했는지 알 수 없다. 따라서, 강화학습의 알고리즘들은 간접적으로라도 이러한 문제를 해결하기 위한 시도를 한다.

강화학습은 대부분 MDP라고 하는 Markov decsion processes로 모델링 된다. MDP란 다음 5개의 튜플을 의미한다.

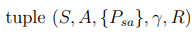
1. S는 set of States 이다. 예로 헬리콥터가 가능한 위치, 방향, 속도 등을 말한다.
2. A는 set of Actions 이다. 예로 체스에서 이동 가능한 모든 말의 움직임을 말한다.
3. $P_{sa}$는 state transition probabilities로 상태 전이 확률을 말한다.
4. $\gamma \in [0, 1)$ 은 discount factor 로 불린다.
5. $R : S \times A \rightarrow \R$ 은 reward function 이다.

예를 들어 다음과 같은 3 X 4 의 미로가 존재하고 어떤 로봇이 이 미로를 움직이고 있다.

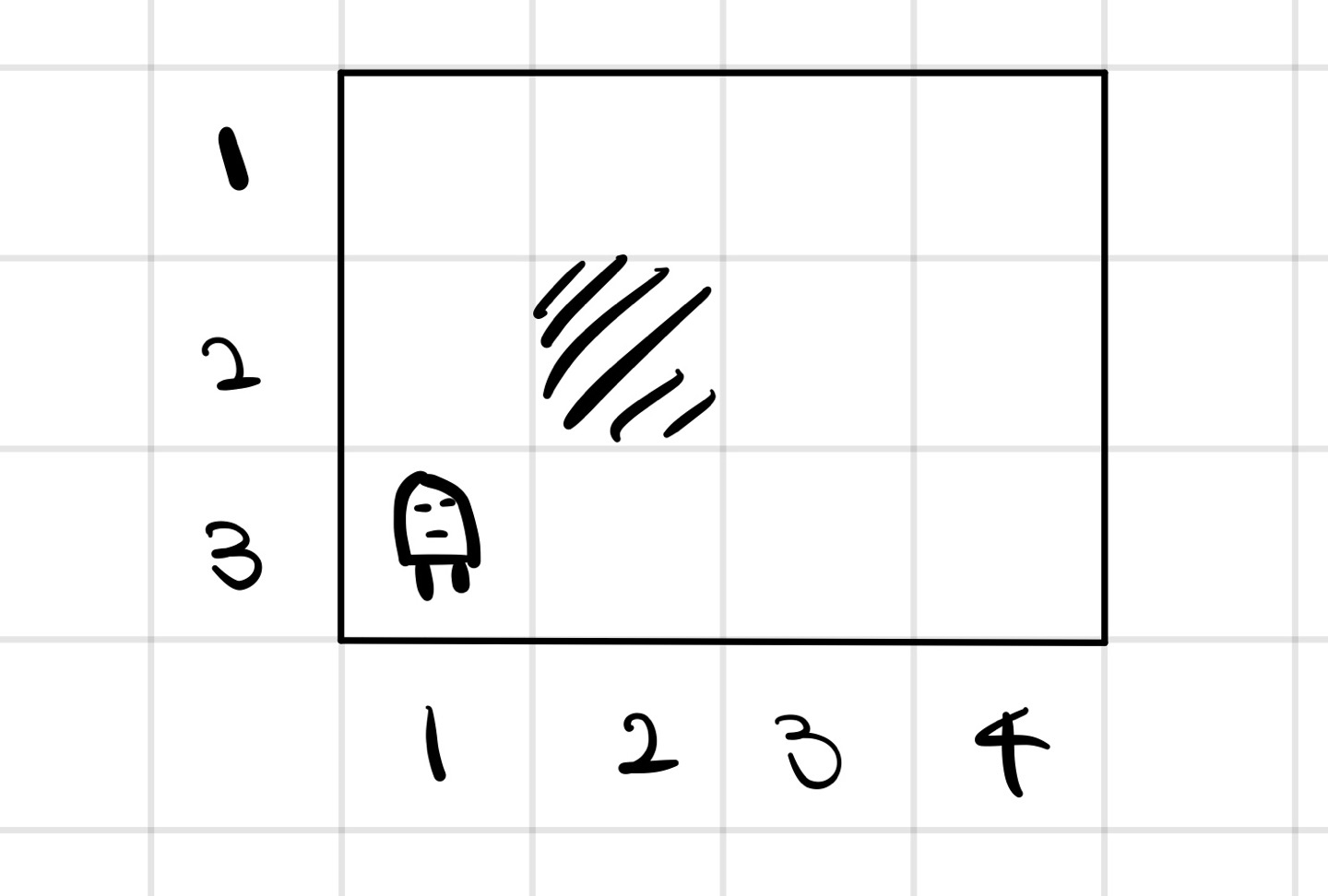
이때 가능한 states는 11이다.

Action = { W,S,E,N} 동서남북이다.

또한, 로봇이 N으로 갈 확률이 0.8, 좌우로 움직일 확률을 각각 0.1로 가정한다.

이때, $P_{3,3} \sim (2,3) = 0. 8$로 쓸 수 있게된다.

이제 (1,4)를 목표로 하기 위해 보상 R((1,4)) = +1 그리고 R((4,2)) = -1 로 정한다.

보상을 설계하는 방법은 여러가지이지만, 일반적으로는 모든 States에 대해 R(s) = -0.02정도의 작은 페널티를 주는 것이다.

이제 이 로봇은 다음과 같은 선택을 반복한다.

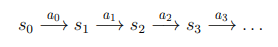
이때 얻게되는 총 보상은 다음과 같이 계산할 수 있다. 감마는 일반적으로 1보다 약간 작도록 선택한다.

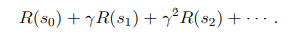
감마를 1보다 약간 작게 할 경우 리워드의 총 합이 무조건 증가하거나 감소하지 않도록 하며 이는 강화학습 알고리즘이 왜 수렴하는지를 일부 증명하는 이유중 하나이다. 또한, 이러한 감마로 인해 시스템이 가능한 빠르게 좋은 결과를 얻도록 유도하는 효과가 있다.

이제 목표는 action들을 골라 예상되는 총 보상을 최대화 시키는 것이다.

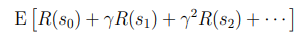
또한, 대부분의 강화학습 알고리즘들은 states에서 action으로 매핑하는 정책을 제시한다. 이는 컨트롤러라 생각하면 된다.

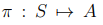
이는 앞선 로봇을 예로들면 $\pi((3,3)) = W$ 로 쓴다면, (3,3)지점에서 West로 action하라는 것을 말한다.