Lecture 17

리치·2023년 5월 21일

CS229

목록 보기

17/21

Lecture 17

Reinforcement Learning and Control

본 강의는 이전 강의였던 Lecture 16의 끝부분과 이어지는 내용이다. 강화학습이란 시행착오를 통해 학습하는 방법이다. 이전의 지도 학습의 경우 정답이 정해져 있는 반면 강화학습의 경우에는 보상을 통해 가중치와 편향을 학습하는 방법이다.

Markov decision processes

Markov decision processes 줄여서 MDP라고 불리는 것은 다음과 같이 정의된다.

$S$ is a set of states.
$A$ is a set of actions.
$P_{sa}$ are the state transition probabilities.
$\gamma \in [0,1)$ is called the discount factor.
$R:S$ x $A$ → $\R$ is the reward function.

위의 MDP의 정의에 대해서는 Lecture 16 에서 다루었으므로 MDP의 과정에 대해서 알아보면 처음에는 $s_0$ 로 시작하고 행동 $a_0 \in A$ 를 취하게 된다. 그리고 그 결과값은 $s_1$ 인데 이 값은 $P_{s_0a_0}$ 를 따르는 값이다. 그런 다음에는 또다른 행동 $a_1$ 취하게 된다. 이러한 일련의 과정을 수식으로 표현하면 다음과 같다.

![Untitled](Lec
ture%2017%20a40dee5753c7494d960a2e95d0405d8e/Untitled.png)

그리고 총 pay-off는 다음과 같다.

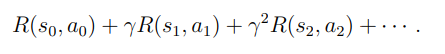
예제를 통해 확인해보면

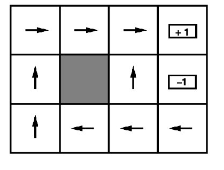
(3,1) 인덱스에서의 state는 ’west’ 이다. 이를 수식으로 표현한다면 $\pi((3,1)) =$ ←(west) 라는 식으로 표현된다.

최적의 정책을 계산하기 위한 알고리즘을 개발하기 위해서는 3가지를 정의해야 한다.

$V^\pi$ is value function
$V^*$ is optimal value function
$\pi^*$ is optimal policy

Value function

Value funtion을 수식으로 표현하면 다음과 같다.

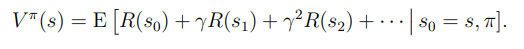
또한 특정한 정책에서의 value finction은 Bellman equation을 만족한다. Bellman equation이란

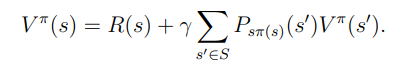
Bellman equation이 어떤식으로 작동하는지 예제를 통해 확인하면 쉽다.

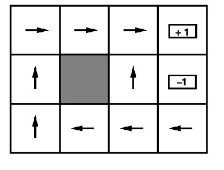
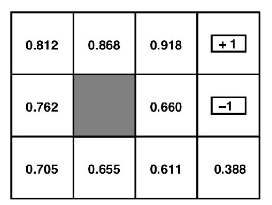
왼쪽의 예제가 state를 표현한 그림이고 오른쪽이 각 state에서의 value값을 나타낸 그림이다. value function을 표현한 오른쪽 그림에서, (3,1)인덱스의 0.611이라는 값은 어떻게 나오게 된 것인지 Bellman equation을 사용하여 확인해보자.

V^\pi((3,1))=R((3,1))+\gamma(0.8V^\pi((2,1))+0.1V^\pi((3,2))+0.1V^\pi((3,1)

위의 식을 bellman equation고 비교해보면 어떤식으로 식이 작동하는지 알 수 있다. value function의 값들은 어떻게 계산할 수 있을까? 그에 대한 해답은 간단하다. bellman equation을 모든 state에서 작성하면 총 11개의 미지수가 생기고 또한 11개의 방정식이 있기 때문에 쉽게 값들을 얻을 수 있다.

Optimal value function

Optimal value function을 정의하면 다음과 같다.

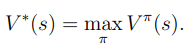
Value function은 특정한 정책에 대한 함수이고 이번에 다룰 Optimal value function은 가능한 모든 정책에 대한 value값을 비교하여 가장 큰 값을 얻는 함수이다. Optimal value function 또한 다른 버전의 bellman equation이 존재한다. 다음은 bellman equation이다.

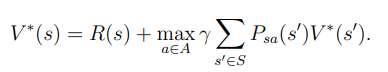
Optimal policy

Value faunciton과 Optimal value function을 살펴보면 어떤게 정책의 최적값인지 알 수 있다.

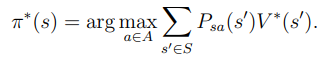
즉 최적의 정책은 우리가 $V^*$ 만 계산할 수 있다면 구할 수 있다.

Value iteration and policy iteration

이제까지 value fucntion이 무엇인지 배웠으므로, 어떻게 구하는지 알아보도록 하자. 최적의 정책을 구하는 방법에는 두가지가 있다. 하나는 value iteration을 통한 방법, 다른 하나는 policy iteration 을 통한 방법이다. 두가지 방법을 들어가기에 앞서 우선 우리가 state transition probabilities 와 reaward function을 안다고 가정하자.

Value iteration

우선 value iteration을 정의하면

For each state $s$ , initialize $V(s): = 0$
for until convergence do
```
  For evey state, update
```

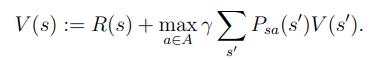
Value iteration을 실행하는 방법에는 두가지가 있다. 첫번째는 synchronous update, 두번째는 asynchronous update 이다. synchronous update이란 모든 state에 대한 value 값을 계산한뒤 한번에 업데이트 하는 방법이다. asynchronous update 방법은 하나의 state당 하나의 value 값을 계산하는 방법이다. 어떠한 방법을 사용해도 $V$ 가 $V^*$ 로 수렴하게 된다.

Policy iteration

Policy iteration을 정의하면

Initialize $\pi$ randomly
for until convergence do
Let $V:=V^\pi$ → typically by linear system solver
For each state s,

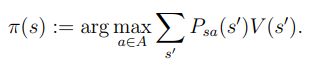
💡 Policy iteraion vs Value iteration

MDPs의 크기가 작은 경우, policy iteration의 경우 적은 반복수로 빠르게 수렴이 가능하다.

MDPs의 크기가 큰 경우, policy iteration에서 매우 큰 연립방정식을 풀게 된다면 계산 비용이 많이 들고 시간도 많이 걸리게 된다. 이러한 경우에는 value iteration을 쓰는게 더 바람직 하다.

Policy iteration 과 Value iteration 모두 MDPs를 풀기 위한 알고리즘 이지만 각각의 장단점이 존재하기에 어떠한 것이 더 좋다고 말할 수 없다.

Learning a model for an MDP

이전까지는 우리가 state transition probabilities 와 reward 를 안다는 가정하에 MDPs를 풀어 나갔다. 하지만 실제 상황에서는 그렇지 않은 경우가 대부분이기 때문에 각각의 값들을 구해야 한다. 이전 예제들 에서는 로봇이 제대로 방향을 찾아갈 확률을 0.8 각각 다른 방향으로 갈 가능성을 0.1로 정하였다. 하지만 실제 상황에서는 로봇이 바닥에서 미끄러 질수도, 아니면 잘못된 방향으로 갈 수도 있기 때문에 정확히 0.8이라는 확률이 나오지 않는다. 따라서 우리는 state transition probabilities를 다음과 같이 정의한다.

💡 Laplace smoothing

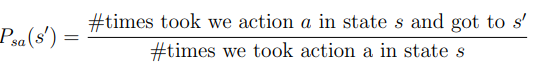
$P_{sa}(s')$ 이 $\frac{0}{0}$ 꼴이 나지 않도록 Laplace smooting을 사용할 수 있지만, 강화학습의 경우에는 0이라는 값이 치명적이지 않은 경우가 많아서 수행하지 않아도 된다.
Laplace smoothing → Laplace smoothing

따라서 다음의 과정들을 통해 MDPs를 해결하는 알고리즘을 완성할 수 있다.

Initialize π randomly.
Repeat {
1. Execute π in the MDP for some number of trials.
  183
2. Using the accumulated experience in the MDP, update our estimates for Psa (and R, if applicable).
3. Apply value iteration with the estimated state transition probabilities and rewards to get a new estimated value function V .
4. Update π to be the greedy policy with respect to V .
  }