Lecture 18

Continuous-state MDP

---

여태까지는 유한한 상태의 MDP에 대해 알아보았다면, 이제는 무한한 상태, 즉 연속적인 상태의 MDP에 대해 알아보자

예를 들어, 자동차의 경우 자동차에는 무한한 경우의 위치가 있기 때문에 state의 개수가 무한하다고 할 수 있다. ****

이 때, MDP를 어떻게 해결할 수 있는지 알아보도록 하자.

1. Discretization

Continuous-State MDP를 쉽게 해결하는 방법은 state space를 discretization하는 것이다

state space를 이산화하고 그 후에 value iteration이나 policy iteration같은 방법을 사용한다.

그러나 이산화를 사용하는 방법은 치명적인 단점 2가지가 있다.

1. 선형회귀의 경우, space를 이산화 하는 것이, 오히려 예측에 도움이 되지 않는다.
   • 데이터의 수가 많고 feature의 수가 적은 경우→ 이산화 하는 것이 나쁘지 않을 수 있다.
   • 그러나 그렇지 않은 경우, 원래의 선형회귀의 경우, 더 function을 부드럽게 만들 수 있음에도 이산화를 쓰면 그렇지 못하기 때문에 좋은 예측을 하지 못하고, 문제가 생긴다.

1. Curse of dimensionality

• 만약에 m개의 차원을 k value로 이산화를 했다면 state의 총 개수는 $k^m$ 개가 된다, 이 문제는 사실 작은 차원 때는 문제가 되지 않지만, 차원의 수가 커진다면 잘 작동하지 않는다.

2. Value function approximation

discretizaiton을 쓰지 않고 continuous-state MDP에서 policy를 찾는 방법인 value function approximation에 대해 알아보자.

value function approximation를 하기 위해서는 model(simulator)이 있어야 한다.

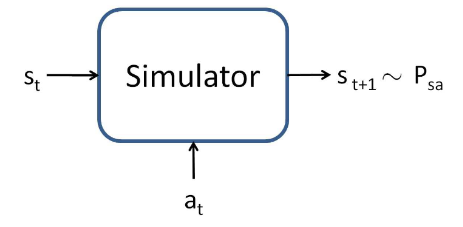
$s_t$는 연속적인 상태이고, $a_t$는 행동이며, simulator의 결과물은 다음 state와 확률 $P_{sa}$이다.

1. model을 만드는 여러가지 방법이 있는 데 그 중에 한 가지 방법은 physics simulator이다.

물리학적 문제에서 여러가지 상태를 알면, 그 때의 그 다음의 상태를 바로 알 수 있다.

예를 들어, 역진자 문제에서, 막대의 길이, 막대의 질량, 기타 등등을 알면 다음 진자의 상태를 알 수 있다.

1. Learn from a data collected in the MDP

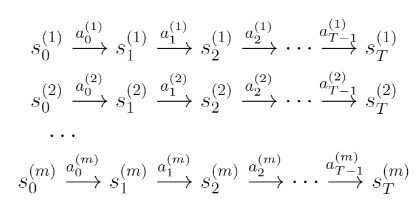
예를 들어, MDP에서 m개의 시도를 할 때, 각각 T개의 timestep이 있다.

이 때, 현재 상태와 현재의 행동을 통해 다음 상태를 예측할 수 있다. 곧,$s_{t+1}=As_t+Ba_t$라고 할 수 있다.

선형회귀의 알고리즘과 비슷하다고 할 수 있기 때문에 위의 A,B는 model의 파라미터라고 할 수 있다.

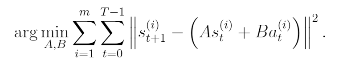
이 때, $s_t$와 $a_t$를 넣었을 때, $s_{t+1}$가 바로 결정 되기 때문에 deterministic model이라고 부른다.

또한, $s_{t+1}$이 랜덤함수의 결과물일 때, stochastic model 라고 한다.

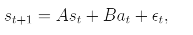
($\epsilon_t$는 noise로서 $\epsilon_t \sim N(0,\sum)$을 따른다.)

지금 까지 알아본 것은 모두 linear function에 대한 것이고,

non-linear function에서도 next state를 구할 수 있다.

$s_{t+1}=A\phi_s(s_t) + B\phi_s(a_t)$라고 할 때, $\phi_s$와$\phi_a$는 non-linear한 feature의 state 와 action의 집합이다.

3. Fitted value iteration

17강의 value iteration과 어떤 것이 다른지 비교하면서 보면 좋을 것 같다.

Fitted value iteration에서는 V(s)를 다음과 같은 식으로 정의할 것이다.

phi는 state의 몇가지 적절한 feature이다.

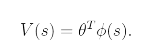
Fitted value iteration의 순서는 다음과 같다.

1. $s^1,s^2,s^3,...s^m\in S$ 랜덤하게 m개의 state를 sampling한다.
2. $\theta$를 0으로 초기화한다.
3. (선형회귀에서는 x→y로의 매핑을 하지만, 여기서는 s→v(s)로의 매핑을 한다.) 다음과 같은 과정을 반복한다.

결론적으로,

Fitted value iteration은 $V^*$에 대한 근사치를 준다.

$\pi^*$는 다음과 같은 식으로 표현 할 수 있기 때문에

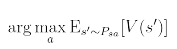
fitted value iteration을 통해 policy 또한 정의할 수 있다.

Computing과 approximating의 과정이 fitted value iteration의 loop 과정과 굉장히 유사하기 때문에, fitted value iteration을 통해 연속적인 state를 가진 상황속에서도 real time optimization 알고리즘을 쓸 수 있다.