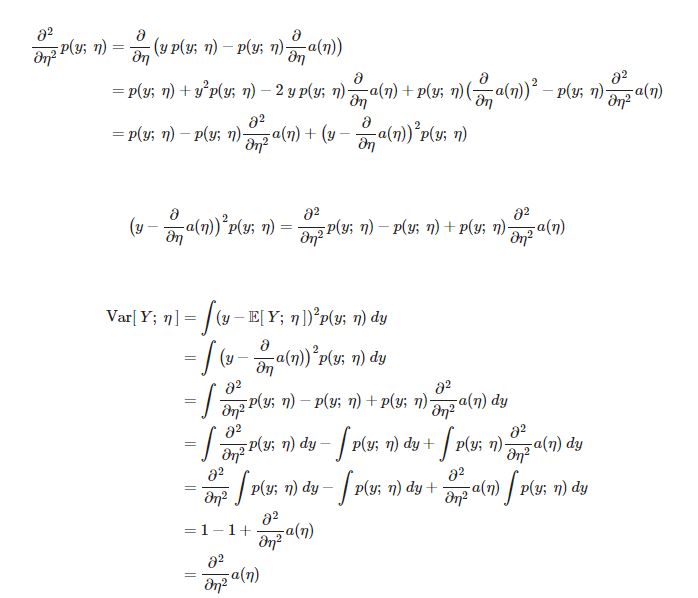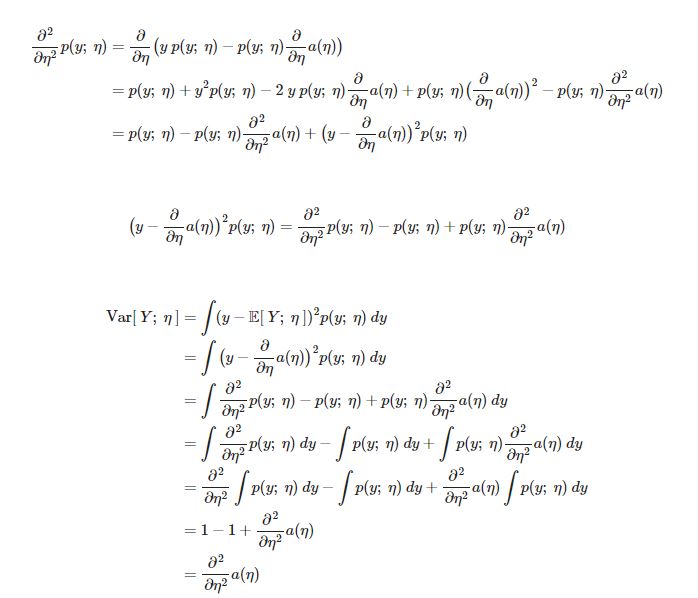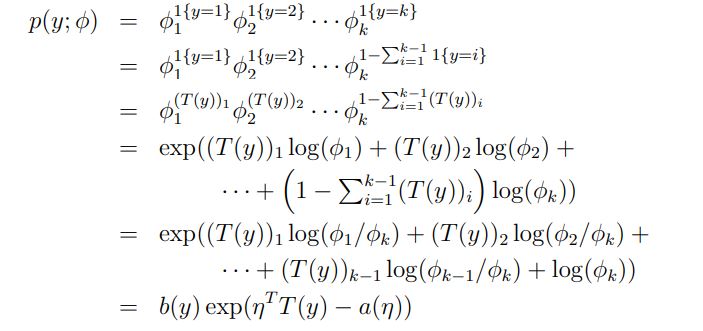deep.daiv 동아리에서 진행했으며 팀원과 함께 정리한 내용입니다.
Lecture 4
Part 3 Generalized Linear Models
지금까지 regression 예제 y∣x;θ N(μ,σ2)와 classification 예제 y∣x;θ Bernoulli(ϕ) 를 살펴보았다.
이번 강의 에서는 두가지 방법이 모두 GLM(Generalized Linear Models)라는 특정한 방법이라는 것임을 밝히고자 한다.
The Exponential family
- GLM 을 배우기 전에, 우리는 exponential family를 정의해야 한다.
p(y;η)=b(y)exp(ηTT(y)−a(η))
η 는 natural parameter(자연 매개변수) 라고 한다.
a(η)는 log partition function(로그분배함수) 이라고 한다.
T(y)는 sufficient statistic라고 부른다. 보통 T(y)=y 로 쓴다.
💡 대부분의 exponential family 예제를 살펴보면 $T(y)=y$ 임을 확인 할 수 있다.
- 베르누이 확률분포 함수를 exponenatial family 형식으로 변경하는 예제
p(y;ϕ)=ϕy(1−ϕ)1−y=exp(ylogϕ+(1−y)log(1−ϕ))=1×exp((log(1−ϕϕ)) + log(1−ϕ)
위의 식을 exponential family와 대조하면서 살펴보면
b(y)=1 , η=log(1−ϕϕ), a(η)=−log(1−ϕ)=log(1+eη) , T(y)=y 가 완성된다.
여기서 η를 ϕ에 관한 식으로 써보면, ϕ=1+e−η1 라는 식이 나오게 되는데 이것은 로지스틱 회귀에서 나왔던 sigmoid 함수와 닮은 형태이다.
그러므로 베르누이 분포를 적절한 T , a, b 를 쓰면 exponential family 형태로 사용이 가능하다.
- 가우스 확률분포 함수를 exponential family 형식으로 변경하는 예제
p(x;μ)=2π1exp(−21(y−μ)2)=2π1exp(−21y2)⋅exp(μy−21μ2)
베르누이 분포와 마찬가지로 exponential family와 대조해보면
η=μ, T(y)=y, a(η)=η2/2=μ2/2, b(y)=(1/2π)exp(−y2/2) 가 완성된다.
💡 σ2 은 선형회귀에서 θ와 hθ(x)를 도출해내는 과정에서 아무런 영향을 주지 않기 때문에 σ2=1이라고 가정한 상태에서 진행하였다.
- Exponential family 를 쓰는 이유
- 자연 매개변수로 매개변수화 된 Exponential family에 대해 최대우도법(maximum likelihood method)를 사용하게 되면 최적화 문제는 항상 위로 볼록한 형태를 그리게 된다.
- E[y;η]=∂η∂a(η) E는 자연 매개변수 η에 의해 매개변수화 된 y의 기대값을 뜻한다.
- Var[y;η]=∂η2∂2a(η) Var는 자연 매개변수 η에 의해 매개변수화 된 y의 분산을 뜻한다.
💡 확률분포의 평균과 분산을 구하기 위해선 무언가를 적분해야 하지만 exponential family에선 로그분배함수 a(η)를 미분하는 것만으로도 기대값과 분산을 구할 수 있다.
-
위의 3가지 이유의 증명
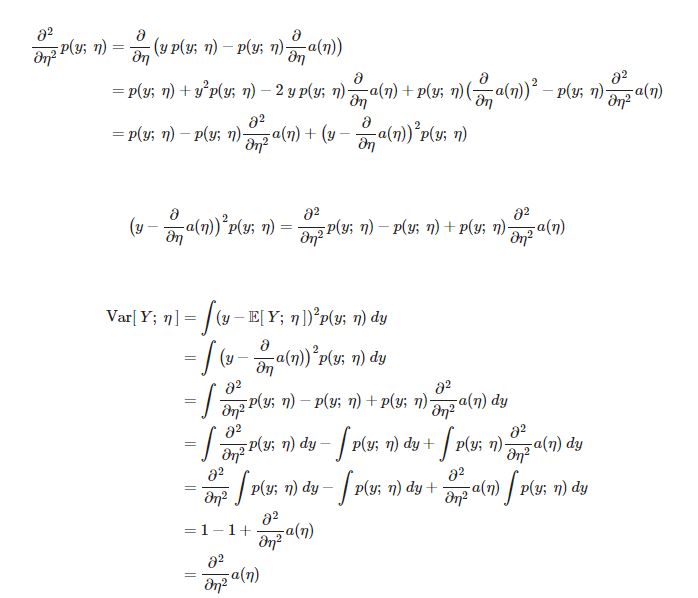
분산증명
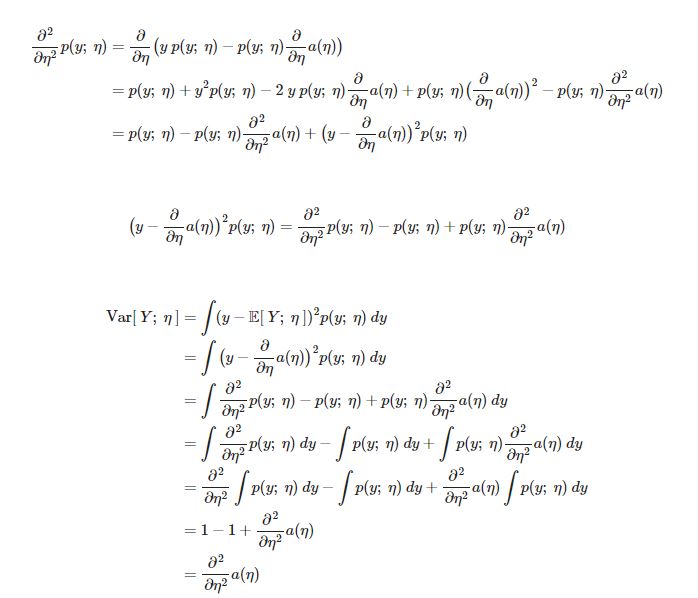
기대값 증명
Constructing GLMs
GLM 을 적용하기 위해선 아래의 3가지 가정이 필연적이다.
-
y∣x;θ ~ Exponential Family(η)
x , θ 와 y의 값을 가지는 분포는 매개변수 η를 가지는 exponential family를 따른다.
-
η=θTx
-
ouput = E[y∣x;θ],
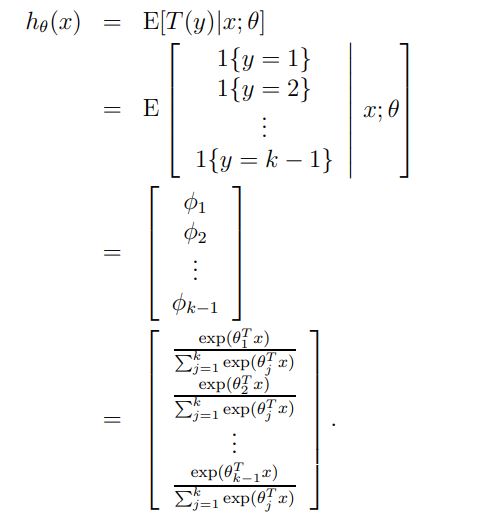
hθ(x)=E[y∣x;θ]
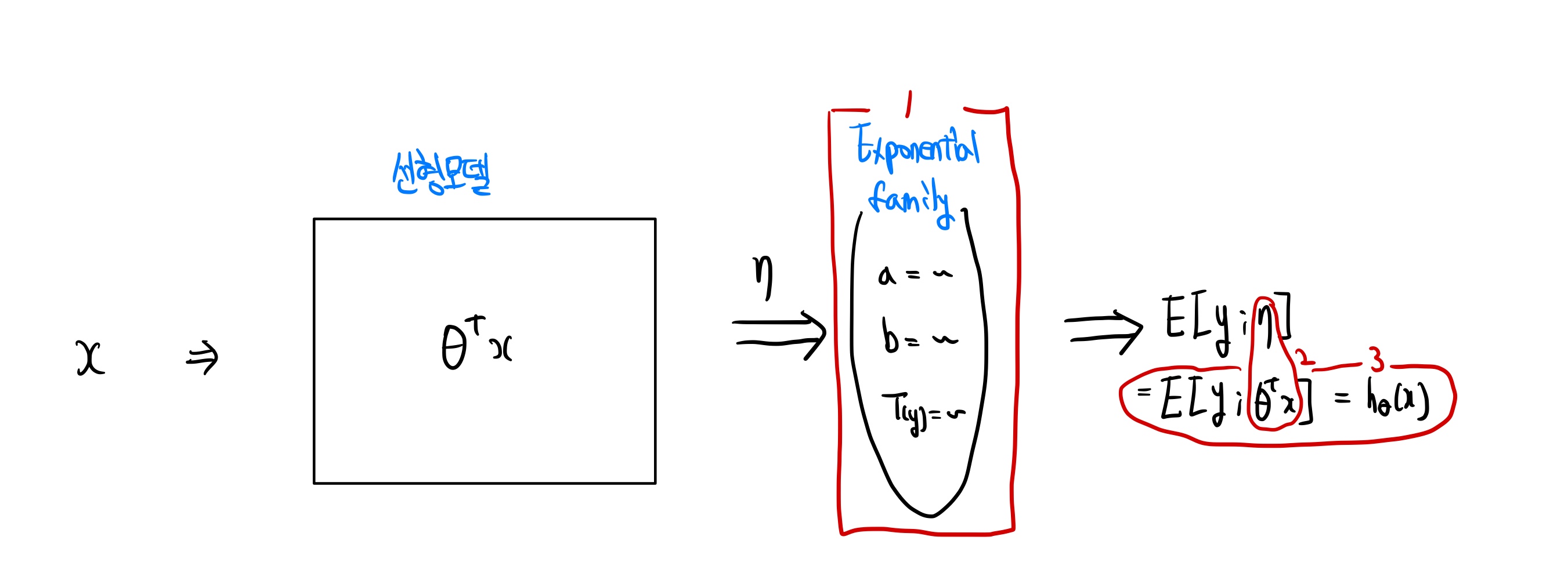
위의 가정들을 시각화 한 그림
💡 E[T(y);η]는 E[y;η]=g(η) 이라는 canonical response function 이라고 불린다.
반대로, g−1는 canonical link function 이라고 부른다.
💡 exponential family의 장점 중 하나였던 E[y;η]=∂η∂a(η) 와 위의 공식을 연결하면
∂η∂a(η)=g(η) 가 된다.
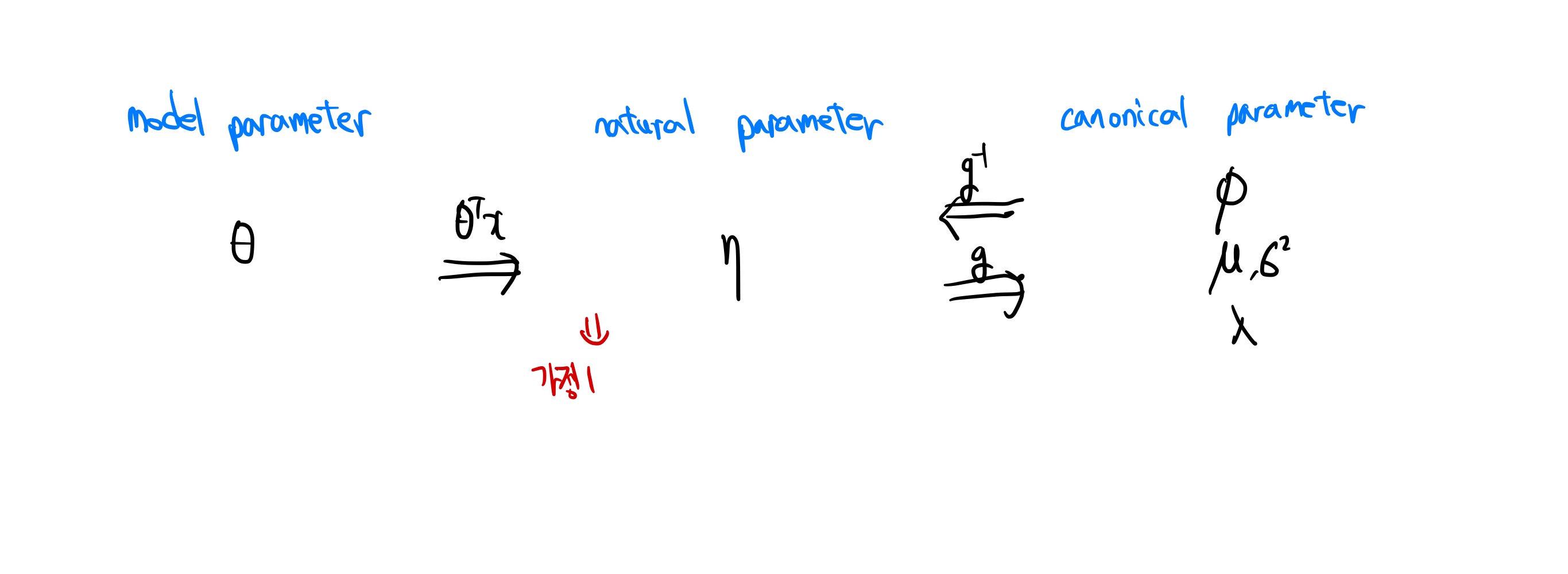
매개변수들 간의 관계를 나타낸 그림
GLM - Logistic Regression
- classification 에선 output y 가 0과 1의 값을 가지므로, 베르누이 분포를 사용하여 모델링 하는것이 자연스럽다.
hθ(x)=E[y∣x;θ]=ϕ=1/(1+e−η)=1/1(1+e−θTx)
- 첫번째 줄은 GLM의 3번째 가정에서 나오게 된 식이고, 베르누이 분포를 따르기 때문에 E[y∣x;θ]=ϕ 라는 식이 나오게 된 것이다.
**이렇게 나온 $h_\theta(x)= 1/1(1+e^{-\theta^Tx})$ 식은 왜 logistic function 이 $1/(1+e^{-z})$인지 알 수 있다.**
GLM - Softmax Regression
Logistic Regression 에서는 ouput y 가 0과1의 값만을 가졌지만, output이 k개라면 어떻게 해야할까?
이산적이고, 여러개의 변수(클래스)를 가지고 있는 경우엔 다항분포(Multinomial distribution)를 사용하는것이 바람직하다. 예제를 통해 softmax regression 이 무엇인지 알아보자.
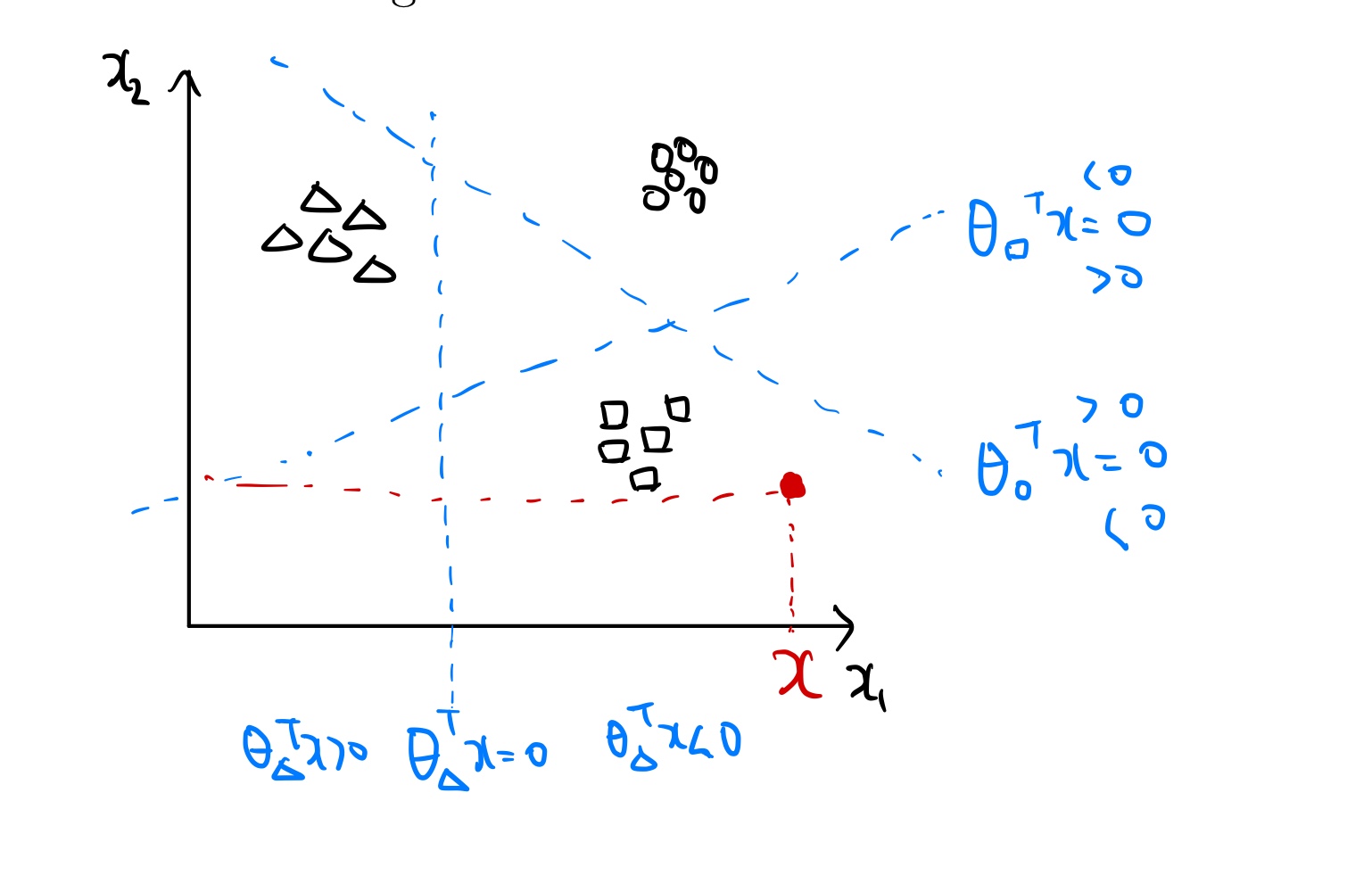
다음과 같이 ouput의 값이 동그라미, 네모, 세모 3가지 모양이 있는 데이터셋이 있다고 가정해보자.
만약우리가 x에서의 출력값은 어떤 변수(클래스)일지 나타내는 확률분포를 구해보자.
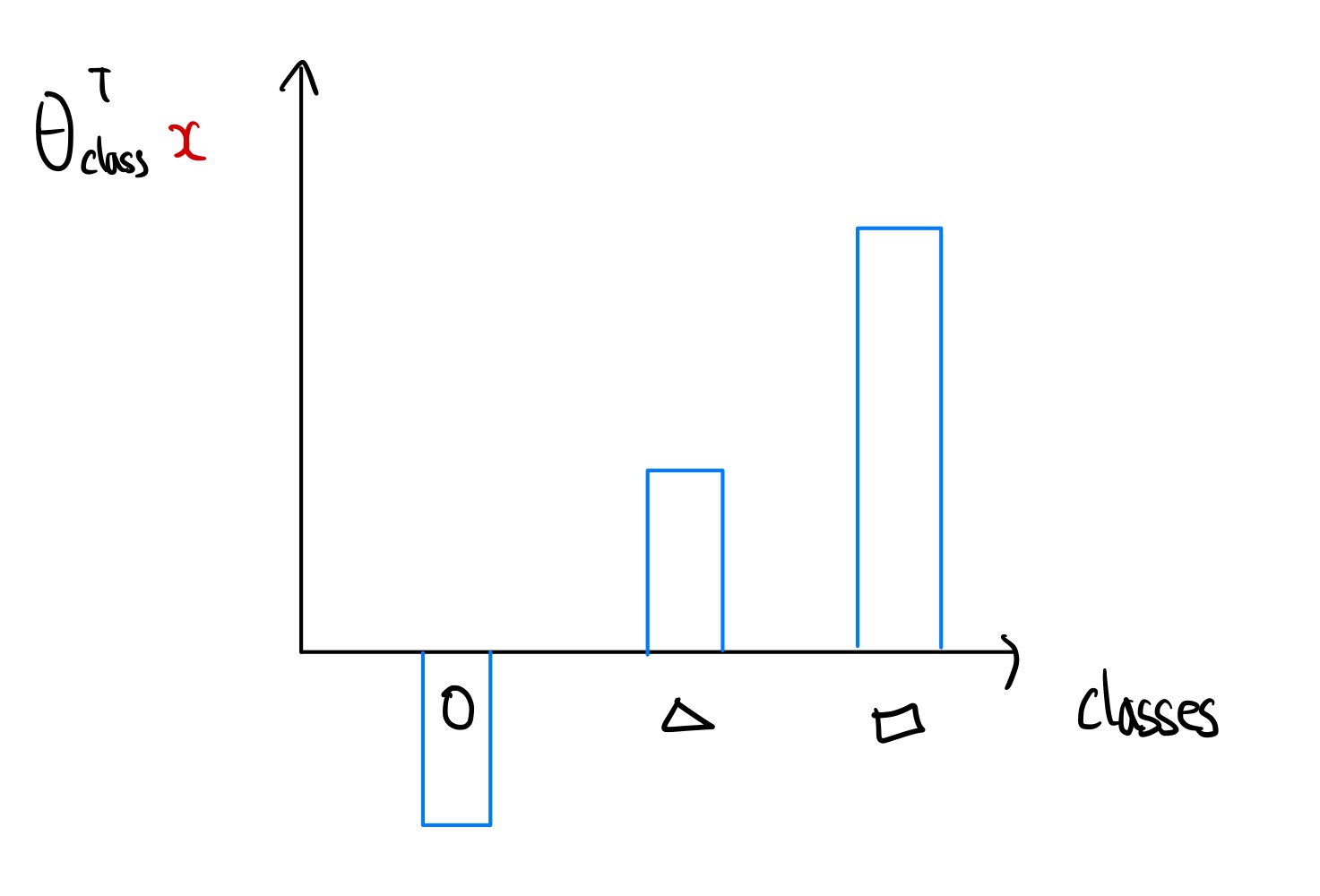
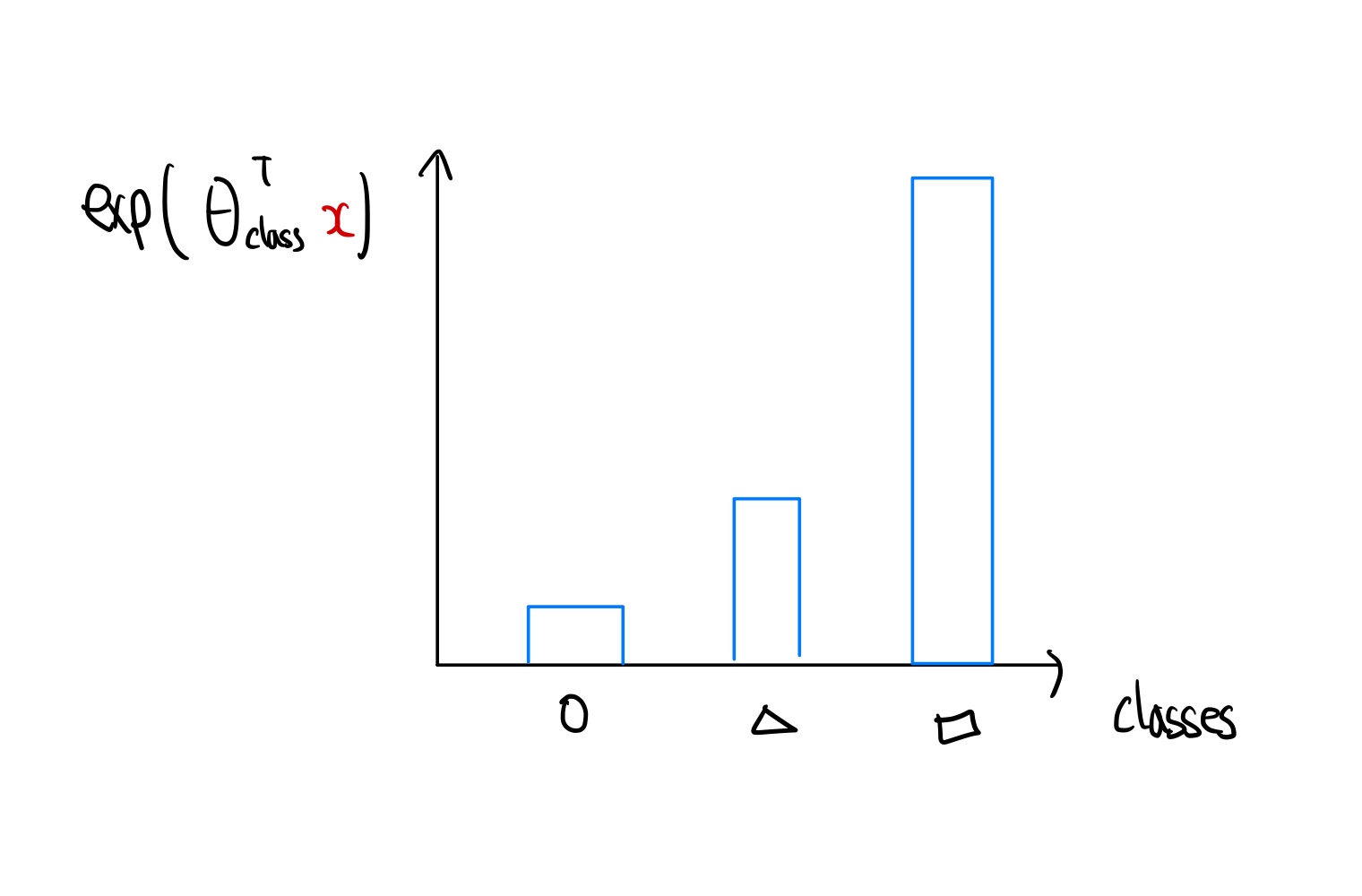
처음 θclassT(x)의 값은 모든 실수값을 가질 수 있다. 따라서 음수의 값을 양수의 값으로 변환하기 위해 모든 결과값에 exp를 취하여 양수로 변환해 준다.
그런다음 각 클래스의 확률값의 합이 1이 되도록 변환해 준다.
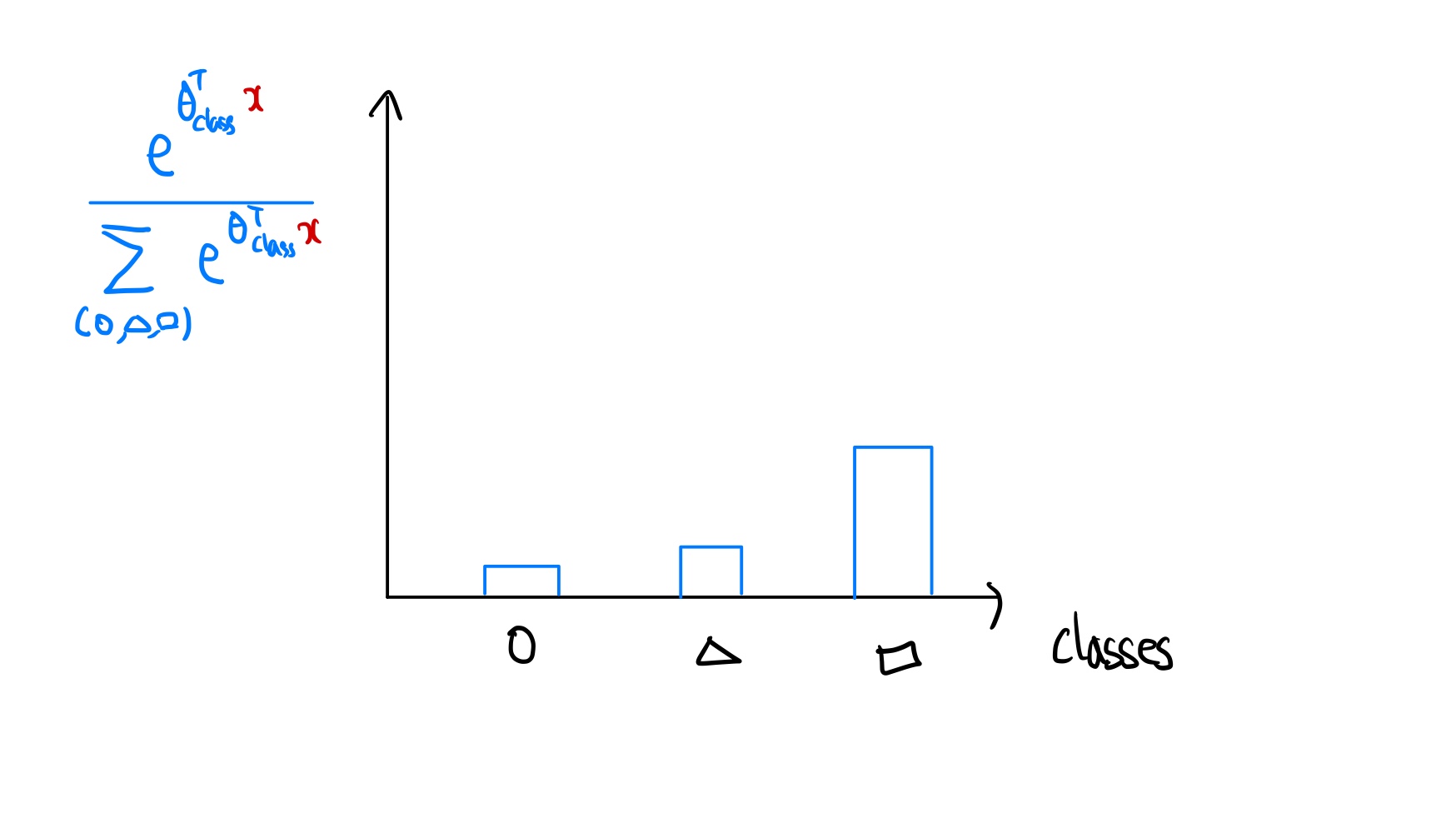
이렇게 각 클래스마다 결과값의 확률의 합이1 인 확률분포로 나타낸 것을 softmax regression 이라고 한다. 다음은 softmax regression을 수학적으로 풀어낸 것이다.
-
다항분포를 exponential family distribution으로 표현해야한다.
T(1)=⎣⎢⎢⎢⎢⎢⎢⎡100⋮0⎦⎥⎥⎥⎥⎥⎥⎤,T(2)=⎣⎢⎢⎢⎢⎢⎢⎡010⋮0⎦⎥⎥⎥⎥⎥⎥⎤,T(k−1)=⎣⎢⎢⎢⎢⎢⎢⎡000⋮1⎦⎥⎥⎥⎥⎥⎥⎤,T(k)=⎣⎢⎢⎢⎢⎢⎢⎡000⋮0⎦⎥⎥⎥⎥⎥⎥⎤
앞에서의 다른 예제들과 달리 $T(y)\ne y$ 이고 $T(y)$는 k-1 차원의 벡터이다.
k-1 차원인 이유는 k차원이 될 경우 각각의 ouput의 확률을 나타내는 매개변수 ϕ1,ϕ2,ϕ3,…,ϕk 가 1{True}=1, 1{False}=1라는 notation 을 사용하여 (T(y))i=1{y=i} 로 표현할 수 있다.
η=⎣⎢⎢⎢⎢⎡log(ϕ1/ϕk)log(ϕ2/ϕk)⋮log(ϕk−1/ϕk)⎦⎥⎥⎥⎥⎤a(η)=−log(ϕk)b(y)=1
- exponential family 로 표현하는 과정
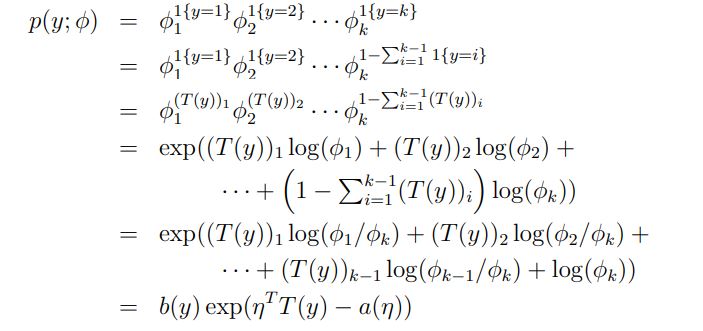
-
Softmax function 구하기
Softmax function이란 각각의 벡터들을 0과1 사이의 값으로 변화하여, 모든 벡터들의 합을 1로 만드는 함수이다.
multinomial distribution 의 link function은 ηi=logϕkϕi로 주어진다. 또한 우리는 ηk=log(ϕk/ϕk)라는 것을 알고있다.
link function을 response function으로 변환하기 위해서는 아래의 과정을 거치면 된다.
eiη=ϕkϕiϕkeηi=ϕiϕkΣi=1keηi=Σi=1kϕi=1ϕ=Σj=1keηjeηi
이렇게 η로 부터 ϕ를 이끌어내는 함수를 softmax 함수라고 한다.
GLM의 2번째 가정인 ηi=θiTx를 사용하면 다음과 같다.
p(y=i∣x;θ)=ϕi=Σj=1keηjeηi=Σj=1keθiTxeθiTx
- ∗∗hθ(x) 구하기**