Lecture 5
Part 4 Generative Learning algorithms
💡 Discriminative learning algorithms : Learn $p(y|x)$ ( or learn $h_\theta(x) = \{0,1\}$ ( x→ y directly) )
Generative learning algorithm : Learn p ( x ∣ y ) p(x|y) p ( x ∣ y ) p ( y ) p(y) p ( y )
Generative learning algorithm 은 p(x|y)와 p(y)를 학습한다. 하지만, 최종적으로 목표로하는 것은 p(y|x)이다. 이를, Bayes rule을 이용해 간접적으로 구한다.
Bayes rule :
p ( y ∣ x ) = p ( x ∣ y ) p ( y ) p ( x ) p ( y = 1 ∣ x ) = p ( x ∣ y = 1 ) p ( y = 1 ) p ( x ) p ( x ) = p ( x ∣ y = 1 ) p ( y = 1 ) + p ( x ∣ y = 0 ) p ( y = 0 ) \begin{aligned} &p(y|x) = \frac{p(x|y)p(y)}{p(x)} \\ &p(y=1|x) = \frac{p(x|y =1)p(y=1)}{p(x)} \\ &p(x) = p(x|y=1)p(y=1)+p(x|y=0)p(y=0) \end{aligned} p ( y ∣ x ) = p ( x ) p ( x ∣ y ) p ( y ) p ( y = 1 ∣ x ) = p ( x ) p ( x ∣ y = 1 ) p ( y = 1 ) p ( x ) = p ( x ∣ y = 1 ) p ( y = 1 ) + p ( x ∣ y = 0 ) p ( y = 0 ) 또한, p(y|x) 를 최대화 시키는 y값을 다음과 같이 표기한다.
a r g m a x y p ( y ∣ x ) = a r g m a x y p ( x ∣ y ) p ( y ) p ( x ) = a r g m a x y p ( x ∣ y ) p ( y ) \begin{aligned} arg\space \underset{y}{max}\space p(y|x) &= arg\space \underset{y}{max}\space \frac{p(x|y)p(y)}{p(x)} \\ &= arg\space \underset{y}{max}\space p(x|y)p(y) \end{aligned} a r g y ma x p ( y ∣ x ) = a r g y ma x p ( x ) p ( x ∣ y ) p ( y ) = a r g y ma x p ( x ∣ y ) p ( y ) 이때, p(x)의 값은 양수이므로 분모값에 상관없이 arg max 값은 오직 분자에 의해서 결정됨을 알 수 있다.
Gaussian Discriminant Analysis (GDA)
Generative learning algorithm에서 살펴볼 첫번째 알고리즘이 GDA이다.
이 모델에서는 다음과 같은 가정이 필요하다.
p ( x ∣ y ) i s d i s t r i b u t e d m u l t i v a r i a t e n o r m a l d i s t r i b u t i o n x ∈ R n a n d x 0 i s n o n e e d s t o b e 1 p(x|y) \space is \space distributed\space multivariate\space normal\space distribution \\ x \in \R^n \space and \space x_0 \space is \space no \space needs \space to\space be \space 1 p ( x ∣ y ) i s d i s t r i b u t e d m u l t i v a r i a t e n o r m a l d i s t r i b u t i o n x ∈ R n a n d x 0 i s n o n e e d s t o b e 1 The multivariate normal distribution
본격적으로 GDA에 들어가기 앞서, 다변량 정규분포의 개념에 대해 이해해야 한다.
다변량 정규분포 z z z
m e a n v e c t o r μ ∈ R n \\mean\space vector \space \mu\in\R^n \space m e a n v e c t o r μ ∈ R n C o v a r i a n c e m a t r i x Σ ∈ R n × n , w h e r e Σ > 0 i s s y m m e t r i c a n d p o s i t i v e s e m i − d e f i n i t e . \space Covariance\space matrix\space \Sigma\in\R^{n \times n}, \space where\space \Sigma >0 \space is \space symmetric \space and \space positive\space semi-definite. C o v a r i a n c e m a t r i x Σ ∈ R n × n , w h e r e Σ > 0 i s s y m m e t r i c a n d p o s i t i v e s e m i − d e f i n i t e .
z ∼ N ( μ ⃗ , Σ ) z ∈ R n z\sim N(\vec\mu, \Sigma) \quad z\in\R^n z ∼ N ( μ , Σ ) z ∈ R n p ( z ) = p ( x ; μ , Σ ) = 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 exp ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) p(z) = p(x;\mu,\Sigma) = \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^-1(x-\mu)) p ( z ) = p ( x ; μ , Σ ) = ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 1 exp ( − 2 1 ( x − μ ) T Σ − 1 ( x − μ ) ) E [ Z ] = ∫ x x p ( x ; μ , Σ ) d x = μ C o v ( Z ) = E [ ( Z − E [ Z ] ) ( Z − E [ Z ] ) T ] = E [ Z Z T ] − ( E [ Z ] ) ( E [ Z ] ) T \begin{aligned} E[Z] &= \int_x xp(x;\mu,\Sigma)dx = \mu \\ Cov(Z) &= E[(Z-E[Z])(Z-E[Z])^T] \\ &=E[ZZ^T] - (E[Z])(E[Z])^T \end{aligned} E [ Z ] C o v ( Z ) = ∫ x x p ( x ; μ , Σ ) d x = μ = E [ ( Z − E [ Z ] ) ( Z − E [ Z ] ) T ] = E [ Z Z T ] − ( E [ Z ] ) ( E [ Z ] ) T
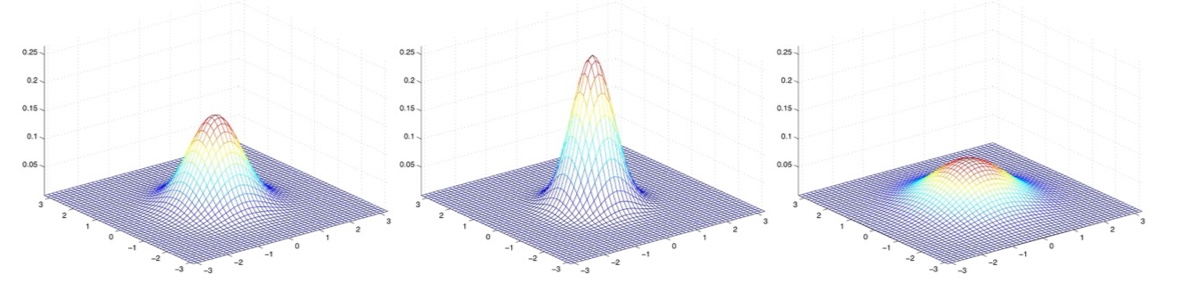
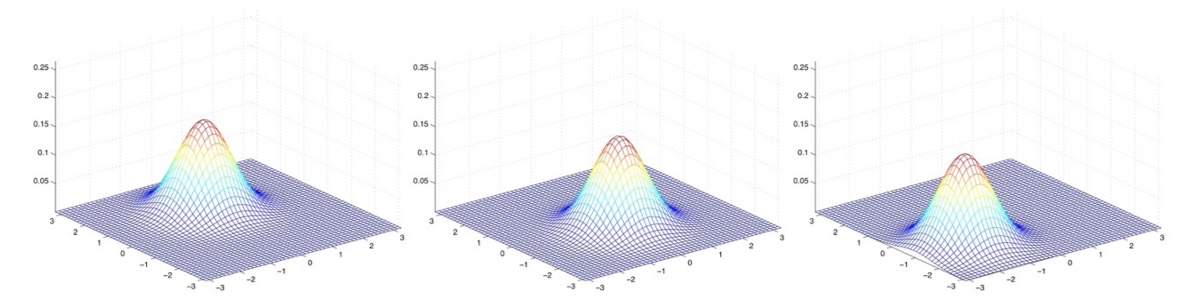
Examples of what the density of a GDA looks like :
μ ⃗ = 0 \vec\mu = 0 μ = 0
평균이 0이고, 공분산이 Identity matrix 일 경우, Standard normal distribution 이라 부른다.
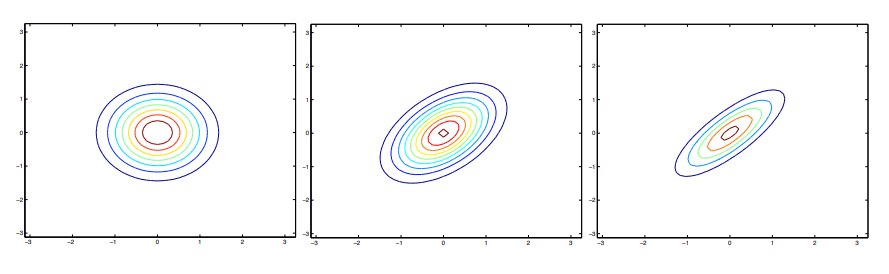
각각 다음과 같은 공분산을 가진다. Σ = [ 1 0 0 1 ] = I \Sigma = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I Σ = [ 1 0 0 1 ] = I Σ = 0.6 I \Sigma = 0.6I Σ = 0 . 6 I Σ = 2 I \Sigma = 2I Σ = 2 I
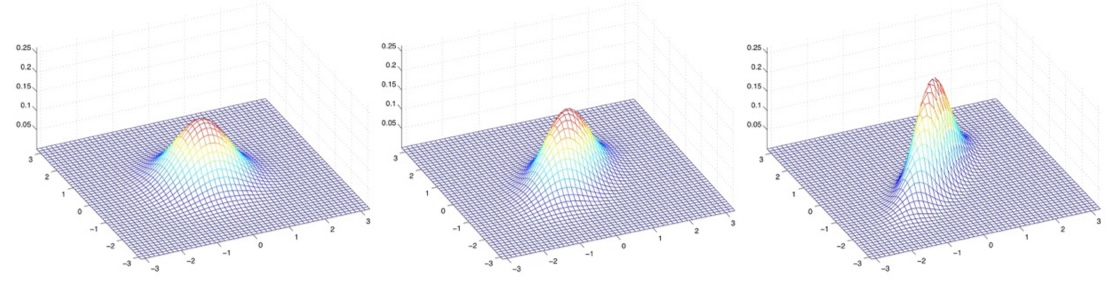
각각 다음과 같은 공분산을 가진다. Σ = I \Sigma = I Σ = I Σ = [ 1 0.5 0.5 1 ] \Sigma = \begin{bmatrix} 1 & 0.5 \\ 0.5 & 1 \end{bmatrix} Σ = [ 1 0 . 5 0 . 5 1 ] Σ = [ 1 0.8 0.8 1 ] \Sigma = \begin{bmatrix} 1 & 0.8 \\ 0.8 & 1 \end{bmatrix} Σ = [ 1 0 . 8 0 . 8 1 ]
이 예제에 대한 등고선은 다음과 같이 그려진다.
첫 번째 그림은 타원이 아니라 완변학 원이다.
다시 공분산에 변화를 주게 되면 다음과 같이 나타난다.
각각 다음과 같은 공분산을 가진다.
Σ = [ 1 − 0.5 − 0.5 1 ] \Sigma = \begin{bmatrix} 1 & -0.5 \\ -0.5 & 1 \end{bmatrix} Σ = [ 1 − 0 . 5 − 0 . 5 1 ] Σ = [ 1 − 0.8 − 0.8 1 ] \Sigma = \begin{bmatrix} 1 & -0.8 \\ -0.8 & 1 \end{bmatrix} Σ = [ 1 − 0 . 8 − 0 . 8 1 ] Σ = [ 3 0.8 0.8 1 ] \Sigma = \begin{bmatrix} 3 & 0.8 \\ 0.8 & 1 \end{bmatrix} Σ = [ 3 0 . 8 0 . 8 1 ]
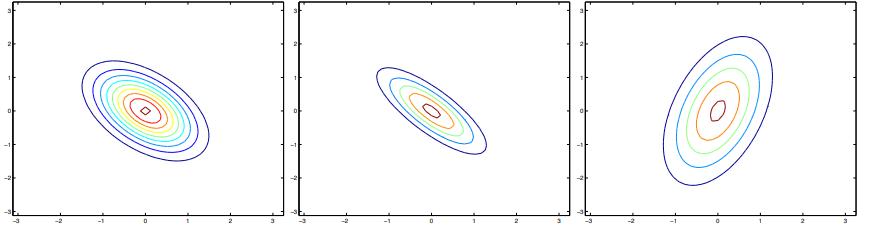
Σ = I \Sigma = I Σ = I μ ⃗ \vec\mu μ
각각 다음과 같은 평균을 가진다. μ = [ 1 0 ] \mu = \begin{bmatrix} 1 \\ 0 \end{bmatrix} μ = [ 1 0 ] μ = [ − 0.5 0 ] \mu = \begin{bmatrix} -0.5 \\ 0 \end{bmatrix} μ = [ − 0 . 5 0 ] μ = [ − 1 − 1.5 ] \mu = \begin{bmatrix} -1 \\ -1.5 \end{bmatrix} μ = [ − 1 − 1 . 5 ]
The Gaussian Discriminant Analysis model
분류 문제(Classification Problem)에서 p ( x ∣ y ) p(x|y) p ( x ∣ y )
이진 분류 문제를 GDA로 모델링 하면 다음과 같다.
Model :
y ∼ B e r n o u l l i ( ϕ ) x ∣ y = 0 ∼ N ( μ 0 , Σ ) x ∣ y = 1 ∼ N ( μ 1 , Σ ) y \sim Bernoulli(\phi) \\ x|y = 0\sim \mathcal{N}(\mu_0,\Sigma) \\x|y = 1\sim \mathcal{N}(\mu_1,\Sigma) y ∼ B e r n o u l l i ( ϕ ) x ∣ y = 0 ∼ N ( μ 0 , Σ ) x ∣ y = 1 ∼ N ( μ 1 , Σ ) 즉, ϕ , Σ , μ 0 , μ 1 \phi,\space \Sigma,\space\mu_0,\space\mu_1 ϕ , Σ , μ 0 , μ 1
About parameters
μ 0 , μ 1 ∈ R n \mu_0 , \space \mu_1 \in \R^n μ 0 , μ 1 ∈ R n Σ ∈ R n × n \Sigma \in \R^{n \times n} Σ ∈ R n × n ϕ ∈ R , 0 ≤ ϕ ≤ 1 \phi \in \R , \space 0 \leq \phi \leq 1 ϕ ∈ R , 0 ≤ ϕ ≤ 1 Σ \Sigma Σ
p ( x ∣ y = 0 ) = 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 exp ( − 1 2 ( x − μ 0 ) T Σ − 1 ( x − μ 0 ) ) p ( x ∣ y = 1 ) = 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 exp ( − 1 2 ( x − μ 1 ) T Σ − 1 ( x − μ 1 ) ) p ( y ) = ϕ y ( 1 − ϕ ) 1 − y p(x|y =0)= \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp(-\frac{1}{2}(x-\mu_0)^T\Sigma^{-1}(x-\mu_0)) \\ p(x|y =1)= \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp(-\frac{1}{2}(x-\mu_1)^T\Sigma{^-1}(x-\mu_1)) \\ p(y) = \phi^y(1-\phi)^{1-y} p ( x ∣ y = 0 ) = ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 1 exp ( − 2 1 ( x − μ 0 ) T Σ − 1 ( x − μ 0 ) ) p ( x ∣ y = 1 ) = ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 1 exp ( − 2 1 ( x − μ 1 ) T Σ − 1 ( x − μ 1 ) ) p ( y ) = ϕ y ( 1 − ϕ ) 1 − y 이 parameter들을 맞추기 위해서 joint likelihood를 최대화 시켜야 한다.
Joint likelihood :
L ( ϕ , μ 0 . μ 1 , Σ ) = ∏ i = 1 m p ( x ( i ) , y ( i ) ; ϕ , μ 0 . μ 1 , Σ ) = ∏ i = 1 m p ( x ( i ) ∣ y ( i ) ; μ 0 . μ 1 , Σ ) p ( y ( i ) ; ϕ ) \begin{aligned} L(\phi,\mu_0.\mu_1,\Sigma) &= \prod_{i=1}^m p(x^{(i)},y^{(i)};\phi,\mu_0.\mu_1,\Sigma) \\ &= \prod_{i=1}^m p(x^{(i)}|y^{(i)};\mu_0.\mu_1,\Sigma)p(y^{(i)};\phi) \end{aligned} L ( ϕ , μ 0 . μ 1 , Σ ) = i = 1 ∏ m p ( x ( i ) , y ( i ) ; ϕ , μ 0 . μ 1 , Σ ) = i = 1 ∏ m p ( x ( i ) ∣ y ( i ) ; μ 0 . μ 1 , Σ ) p ( y ( i ) ; ϕ )
Difference between Discriminative learning algorithm Conditional likelihood : L ( θ ) = ∏ i = 1 m p ( y ( i ) ∣ x ( i ) ; θ ) L(\theta) = \prod_{i=1}^m p(y^{(i)}|x^{(i)};\theta) L ( θ ) = i = 1 ∏ m p ( y ( i ) ∣ x ( i ) ; θ ) θ \theta θ
이제 MLE를 사용하여, likelihood를 최대화 시키는 매개변수 값을 얻을 수 있다.
ϕ = 1 m ∑ i = 1 m 1 { y ( i ) = 1 } μ 0 = ∑ i = 1 m 1 { y ( i ) = 0 } x ( i ) ∑ i = 1 m 1 { y ( i ) = 0 } μ 1 = ∑ i = 1 m 1 { y ( i ) = 1 } x ( i ) ∑ i = 1 m 1 { y ( i ) = 1 } Σ = 1 m ∑ i = 1 m ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T \phi = \frac{1}{m}\sum_{i=1}^m1\{{y^{(i)}=1\}} \\ \mu_0 = \frac{\sum_{i=1}^m1\{{y^{(i)}=0\}}x^{(i)}}{\sum_{i=1}^m1\{{y^{(i)}=0\}}} \\ \mu_1 = \frac{\sum_{i=1}^m1\{{y^{(i)}=1\}}x^{(i)}}{\sum_{i=1}^m1\{{y^{(i)}=1\}}} \\ \Sigma = \frac{1}{m}\sum_{i=1}^m(x^{(i)}-\mu_{y^{(i)}})(x^{(i)}-\mu_{y^{(i)}})^T ϕ = m 1 i = 1 ∑ m 1 { y ( i ) = 1 } μ 0 = ∑ i = 1 m 1 { y ( i ) = 0 } ∑ i = 1 m 1 { y ( i ) = 0 } x ( i ) μ 1 = ∑ i = 1 m 1 { y ( i ) = 1 } ∑ i = 1 m 1 { y ( i ) = 1 } x ( i ) Σ = m 1 i = 1 ∑ m ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T
How to calculate ?
Note that :
μ y ( i ) = 1 { y ( i ) = 0 } μ 0 + 1 { y ( i ) = 1 } μ 1 p ( x ( i ) ∣ y ( i ) ; μ 0 , μ 1 , Σ ) = 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 e x p ( − 1 2 ( x ( i ) − μ y ( i ) ) T Σ − 1 ( x ( i ) − μ y ( i ) ) ) p ( y ( i ) ; ϕ ) = ϕ 1 { y ( i ) = 1 } ( 1 − ϕ ) 1 − 1 { y ( i ) = 1 } \mu_{y^{(i)}}= 1\{{y^{(i)}}=0\}\mu_0+1\{{y^{(i)}}=1\}\mu_1 \\ p(x^{(i)}|y^{(i)};\mu_0,\mu_1,\Sigma) = \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}exp(-\frac{1}{2}(x^{(i)}-\mu_{y^{(i)}})^T\Sigma^{-1}(x^{(i)}-\mu_{y^{(i)}})) \\ p(y^{(i)};\phi) = \phi^{1\{y^{{(i)}=1}\}}(1-\phi)^{1-{1\{y^{{(i)}=1}\}}} μ y ( i ) = 1 { y ( i ) = 0 } μ 0 + 1 { y ( i ) = 1 } μ 1 p ( x ( i ) ∣ y ( i ) ; μ 0 , μ 1 , Σ ) = ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 1 e x p ( − 2 1 ( x ( i ) − μ y ( i ) ) T Σ − 1 ( x ( i ) − μ y ( i ) ) ) p ( y ( i ) ; ϕ ) = ϕ 1 { y ( i ) = 1 } ( 1 − ϕ ) 1 − 1 { y ( i ) = 1 } L e t l ( ( ϕ , μ 0 . μ 1 , Σ ) ) = l o g L ( ϕ , μ 0 . μ 1 , Σ ) Let \space l((\phi,\mu_0.\mu_1,\Sigma)) = log \space L(\phi,\mu_0.\mu_1,\Sigma) L e t l ( ( ϕ , μ 0 . μ 1 , Σ ) ) = l o g L ( ϕ , μ 0 . μ 1 , Σ )
l ( ( ϕ , μ 0 . μ 1 , Σ ) = ∑ i = 1 m l o g p ( x ( i ) ∣ y ( i ) ; μ 0 , μ 1 , Σ ) + ∑ i = 1 m l o g p ( y ( i ) ; ϕ ) = ∑ i = 1 m l o g 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 e x p ( − 1 2 ( x ( i ) − μ y ( i ) ) T Σ − 1 ( x ( i ) − μ y ( i ) ) ) + ∑ i = 1 m l o g ϕ 1 { y ( i ) = 1 } ( 1 − ϕ ) 1 − 1 { y ( i ) = 1 } \begin{aligned} l((\phi,\mu_0.\mu_1,\Sigma) &= \sum_{i=1}^m log\space p(x^{(i)}|y^{(i)};\mu_0,\mu_1,\Sigma) +\sum_{i=1}^m log\space p(y^{(i)};\phi) \\ &= \sum_{i=1}^m log\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}exp(-\frac{1}{2}(x^{(i)}-\mu_{y^{(i)}})^T\Sigma^{-1}(x^{(i)}-\mu_{y^{(i)}})) \\ &\qquad + \sum_{i=1}^m log\space \phi^{1\{y^{{(i)}=1}\}}(1-\phi)^{1-{1\{y^{{(i)}=1}\}}} \\ \end{aligned} l ( ( ϕ , μ 0 . μ 1 , Σ ) = i = 1 ∑ m l o g p ( x ( i ) ∣ y ( i ) ; μ 0 , μ 1 , Σ ) + i = 1 ∑ m l o g p ( y ( i ) ; ϕ ) = i = 1 ∑ m l o g ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 1 e x p ( − 2 1 ( x ( i ) − μ y ( i ) ) T Σ − 1 ( x ( i ) − μ y ( i ) ) ) + i = 1 ∑ m l o g ϕ 1 { y ( i ) = 1 } ( 1 − ϕ ) 1 − 1 { y ( i ) = 1 } By using log properties,
= − m n 2 l o g ( 2 π ) − m 2 l o g ∣ Σ ∣ − 1 2 ∑ i = 1 m ( x ( i ) − μ y ( i ) ) T Σ − 1 ( x ( i ) − μ y ( i ) ) + ∑ i = 1 m 1 { y ( i ) = 1 } l o g ϕ + ( m − ∑ i = 1 m { y ( i ) = 1 } ) l o g ( 1 − ϕ ) \begin{aligned} &= -\frac{mn}{2}log(2\pi)-\frac{m}{2}log|\Sigma|-\frac{1}{2}\sum_{i=1}^m (x^{(i)}-\mu_{y^{(i)}})^T\Sigma^{-1}(x^{(i)}-\mu_{y^{(i)}}) \\ \\ &\qquad + \sum_{i=1}^m1\{{y^{(i)}=1\}}log\phi+(m-\sum_{i=1}^m \{{y^{(i)}=1\}})log(1-\phi) \end{aligned} = − 2 m n l o g ( 2 π ) − 2 m l o g ∣ Σ ∣ − 2 1 i = 1 ∑ m ( x ( i ) − μ y ( i ) ) T Σ − 1 ( x ( i ) − μ y ( i ) ) + i = 1 ∑ m 1 { y ( i ) = 1 } l o g ϕ + ( m − i = 1 ∑ m { y ( i ) = 1 } ) l o g ( 1 − ϕ )
Taking the partial derivative for each variable,
∂ l ∂ μ y ( i ) = Σ − 1 ∑ i = 1 m ( x ( i ) − μ y ( i ) ) ∂ μ y ( i ) ∂ μ 0 = 1 { y ( i ) = 0 } , ∂ μ y ( i ) ∂ μ 1 = 1 { y ( i ) = 1 } \frac{\partial l}{\partial\mu_{y^{(i)}}} = \Sigma^{-1} \sum_{i=1}^m(x^{(i)}-\mu_{y^{(i)}}) \\ \frac{\partial\mu_{y^{(i)}}}{\partial\mu_0} = 1\{{y^{(i)}}=0\}, \frac{\partial\mu_{y^{(i)}}}{\partial\mu_1} = 1\{{y^{(i)}}=1\} ∂ μ y ( i ) ∂ l = Σ − 1 i = 1 ∑ m ( x ( i ) − μ y ( i ) ) ∂ μ 0 ∂ μ y ( i ) = 1 { y ( i ) = 0 } , ∂ μ 1 ∂ μ y ( i ) = 1 { y ( i ) = 1 } ∂ l ∂ ϕ = 1 ϕ ∑ i = 1 m 1 { y ( i ) = 1 } + 1 ϕ − 1 ( m − ∑ i = 1 m 1 { y ( i ) = 1 } ) ∂ l ∂ μ 0 = ∂ l ∂ μ y ( i ) ∂ μ y ( i ) ∂ μ 0 = Σ − 1 ∑ i = 1 m ( x ( i ) 1 { y ( i ) = 0 } − μ y ( i ) 1 { y ( i ) = 0 } ) ∂ l ∂ Σ = − m 2 Σ − 1 + 1 2 Σ − 1 ( ∑ i = 1 m ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T ) Σ − 1 \frac{\partial l}{\partial\phi} = \frac{1}{\phi}\sum_{i=1}^m1\{{y^{(i)}=1\}} + \frac{1}{\phi-1}(m-\sum_{i=1}^m1\{{y^{(i)}=1\}}) \\ \frac{\partial l}{\partial\mu_0} = \frac{\partial l}{\partial\mu_{y^{(i)}}} \frac{\partial\mu_{y^{(i)}}}{\partial\mu_0} = \Sigma^{-1} \sum_{i=1}^m(x^{(i)}1\{{y^{(i)}}=0\}-\mu_{y^{(i)}}1\{{y^{(i)}}=0\}) \\ \frac{\partial l}{\partial\Sigma} = -\frac{m}{2}\Sigma^{-1}+\frac{1}{2}\Sigma^{-1}(\sum_{i=1}^m (x^{(i)}-\mu_{y^{(i)}})(x^{(i)}-\mu_{y^{(i)}})^T)\Sigma^{-1} ∂ ϕ ∂ l = ϕ 1 i = 1 ∑ m 1 { y ( i ) = 1 } + ϕ − 1 1 ( m − i = 1 ∑ m 1 { y ( i ) = 1 } ) ∂ μ 0 ∂ l = ∂ μ y ( i ) ∂ l ∂ μ 0 ∂ μ y ( i ) = Σ − 1 i = 1 ∑ m ( x ( i ) 1 { y ( i ) = 0 } − μ y ( i ) 1 { y ( i ) = 0 } ) ∂ Σ ∂ l = − 2 m Σ − 1 + 2 1 Σ − 1 ( i = 1 ∑ m ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T ) Σ − 1 To maximizing, the value of each partial derivative should be set to zero.
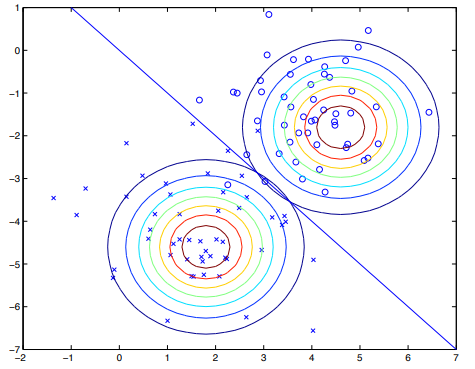
알고리즘은 다음과 같은 모습을 보이게 된다.
우선, 각 클래스에 대해 Gaussian을 설정하면, 다음과 같은 등고선 그려진다. 이후, 각 점에 대해서 Bayes rule을 사용한 후, 경계를 결정하면 다음과 같은 직선이 그려진다. Discriminative learning algorithm 중 하나인 logistic regression이 그리는 경계선과 약간 다르며, 서로 도달하는 방식 역시 다르다.
이 예제에서는 서로다른 평균 μ 0 , μ 1 \mu_0, \mu_1 μ 0 , μ 1 Σ \Sigma Σ
Discussion : GDA and logistic regression
ϕ , μ 0 , μ 1 , Σ \phi, \mu_0,\mu_1,\Sigma ϕ , μ 0 , μ 1 , Σ p ( y = 1 ∣ x ; ϕ , μ 0 , μ 1 , Σ ) p(y=1|x;\phi,\mu_0,\mu_1,\Sigma) p ( y = 1 ∣ x ; ϕ , μ 0 , μ 1 , Σ )
p ( y = 1 ∣ x ; ϕ , μ 0 μ 1 , Σ ) = 1 1 + exp ( − ( θ T x + θ 0 ) ) w h e r e θ ∈ R n a n d θ 0 ∈ R p(y=1|x;\phi,\mu_0\mu_1,\Sigma) = \frac{1}{1+\exp(-(\theta^Tx+\theta_0))} \\ where \space \theta\in\R^n\space and \space \theta_0\in\R p ( y = 1 ∣ x ; ϕ , μ 0 μ 1 , Σ ) = 1 + exp ( − ( θ T x + θ 0 ) ) 1 w h e r e θ ∈ R n a n d θ 0 ∈ R
How to get θ , θ 0 ? \theta,\theta_0 ? θ , θ 0 ? p ( y = 1 ∣ x ) = p ( x ∣ y = 1 ) p ( y = 1 ) p ( x ∣ y = 1 ) p ( y = 1 ) + p ( x ∣ y = 0 ) p ( y = 0 ) \begin{aligned} p(y=1|x) &= \frac{p(x|y =1)p(y=1)}{p(x|y=1)p(y=1)+p(x|y=0)p(y=0) } \end{aligned} p ( y = 1 ∣ x ) = p ( x ∣ y = 1 ) p ( y = 1 ) + p ( x ∣ y = 0 ) p ( y = 0 ) p ( x ∣ y = 1 ) p ( y = 1 ) = exp ( − 1 2 ( x − μ 1 ) T Σ − 1 ( x − μ 1 ) ) ϕ exp ( − 1 2 ( x − μ 1 ) T Σ − 1 ( x − μ 1 ) ) ϕ + exp ( − 1 2 ( x − μ 0 ) T Σ − 1 ( x − μ 0 ) ) ( 1 − ϕ ) = 1 1 + exp ( 1 2 ( x − μ 1 ) T Σ − 1 ( x − μ 1 ) − 1 2 ( x − μ 0 ) T Σ − 1 ( x − μ 0 ) ) 1 − ϕ ϕ \begin{aligned} &= \frac{\exp(-\frac{1}{2}(x-\mu_1)^T\Sigma^{-1}(x-\mu_1))\phi}{\exp(-\frac{1}{2}(x-\mu_1)^T\Sigma^{-1}(x-\mu_1))\phi+\exp(-\frac{1}{2}(x-\mu_0)^T\Sigma^{-1}(x-\mu_0))(1-\phi)} \\ &= \frac{1}{1+\exp(\frac{1}{2}(x-\mu_1)^T\Sigma^{-1}(x-\mu_1)-\frac{1}{2}(x-\mu_0)^T\Sigma^{-1}(x-\mu_0))\frac{1-\phi}{\phi}} \end{aligned} = exp ( − 2 1 ( x − μ 1 ) T Σ − 1 ( x − μ 1 ) ) ϕ + exp ( − 2 1 ( x − μ 0 ) T Σ − 1 ( x − μ 0 ) ) ( 1 − ϕ ) exp ( − 2 1 ( x − μ 1 ) T Σ − 1 ( x − μ 1 ) ) ϕ = 1 + exp ( 2 1 ( x − μ 1 ) T Σ − 1 ( x − μ 1 ) − 2 1 ( x − μ 0 ) T Σ − 1 ( x − μ 0 ) ) ϕ 1 − ϕ 1 N o t e : 1 − ϕ ϕ = exp ( log ( 1 − ϕ ϕ ) Note \space : \frac{1-\phi}{\phi} = \exp(\log(\frac{1-\phi}{\phi}) N o t e : ϕ 1 − ϕ = exp ( log ( ϕ 1 − ϕ ) θ = Σ − 1 ( u 1 − μ 0 ) θ 0 = 1 2 ( μ + 0 + μ 1 ) T Σ − 1 ( μ 0 − μ 1 ) − log ( 1 − ϕ ϕ ) \begin{aligned} &\theta = \Sigma^{-1}(\,u_1-\mu_0) \\ &\theta_0 = \frac{1}{2}(\mu+0+\mu_1)^T\Sigma^{-1}(\mu_0-\mu_1)-\log(\frac{1-\phi}{\phi}) \end{aligned} θ = Σ − 1 ( u 1 − μ 0 ) θ 0 = 2 1 ( μ + 0 + μ 1 ) T Σ − 1 ( μ 0 − μ 1 ) − log ( ϕ 1 − ϕ )
Logistic regression 에서 p(y=1|x) 를 구할 때와 동일한 모습을 보인다. (그러나, 앞서 말했듯 실제로 알고리즘이 나타내는 결정경계는 조금 다른 형태를 띄게 된다.)
GDA 모델에서 p(x|y)를 Gaussian이라 가정하고, y는 베르누이 분포를 따른다고 가정한다. 이때, p(y=1|x)는 logistic regression을 따름을 증명하였다. 그러나, p(y|x) 가 logistic regression일 때, p(x|y)가 꼭 Gaussian을 나타내지는 않는다. 이를 바탕으로, GDA의 가정이 strong assumption이고 logistic regression은 weak assumption이 된다.
이러한 이유로 데이터 셋이 Gaussian이더라도 logistic regression을 사용하는 것은 GDA와 비슷한 결과를 도출한다. 하지만, 분명하게 데이터 셋이 Gaussian임을 알 고 있다면 GDA 모델을 사용하는 것이 데이터에 관해 더 많은 정보를 주게 되는 것이므로 더 잘 작동하며 효율적이다. 즉, 모델링에 있어 strong assumption이 맞다면, weak assumption 보다 더 잘 작동하지만, 일반적으로는 logistic regression 사용을 권장한다. ( 데이터 셋이 적다면, GDA도 잘 작동한다.)
비슷하게 p(x|y)가 Poisson이며, y는 베르누이 분포를 따라갈 때, p(y|x)가 logistic 임을 증명할 수 있다.
Naive Bayes
이 알고리즘은 이메일 스팸분류를 예시로 들어 설명한다.
우선, 사전에 n개의 단어가 있다고 가정한다. 그리고, 이메일의 텍스트에 사전에 있는 단어가 있다면 1로 없다면 0으로 하는 벡터 x를 만든다.
x = [ 1 0 0 ⋮ 1 ⋮ 0 ] { a a a r d v a r a a r d w o l f ⋮ b u y ⋮ z y g m u r g y n t h x= \begin{bmatrix} 1 \\ 0 \\ 0 \\ \vdots \\ 1 \\ \vdots \\0 \end{bmatrix} \begin{cases} a \\ aardvar\\aardwolf\\ \vdots \\ buy \\ \vdots \\ zygmurgy \end{cases} n^{th} x = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 0 0 ⋮ 1 ⋮ 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ a a a r d v a r a a r d w o l f ⋮ b u y ⋮ z y g m u r g y n t h 따라서, x ∈ { 0 , 1 } n x \in \{0,1\}^n x ∈ { 0 , 1 } n x i = 1 { w o r d i a p p e a r s i n e m a i l } x_i = 1\{word\space i\space appears\space in\space email\} x i = 1 { w o r d i a p p e a r s i n e m a i l }
이제 Generative learning algorithm에서 p(x|y)와 p(y)를 모델링 해야한다. 하지만, x가 될 수 있는 경우의 수는 2 n 2^n 2 n 2 n − 1 2^n-1 2 n − 1
x i ′ s a r e c o n d i t i o n a l l y i n d e p e n d e n t g i v e y x_i\space's \space are\space conditionally\space independent\space give\space y x i ′ s a r e c o n d i t i o n a l l y i n d e p e n d e n t g i v e y 이 가정과 확률의 연쇄법칙을 사용하면 다음과 같이 나타난다.
p ( x 1 , ⋯ , x n ∣ y ) = p ( x 1 ∣ y ) p ( x 2 ∣ y , x 1 ) ⋯ p ( x n ∣ y , x 1 , ⋯ , x n − 1 ) = p ( x 1 ∣ y ) p ( x 2 ∣ y ) ⋯ p ( x n ∣ y ) ( b y a s s u m p t i o n ) = ∏ i = 1 n p ( x i ∣ y ) \begin{aligned} p(x_1, \cdots,x_n|y) &= p(x_1|y)p(x_2|y,x1)\cdots p(x_n|y,x_1,\cdots,x_{n-1}) \\ &= p(x_1|y)p(x_2|y)\cdots p(x_n|y) \quad (by \space assumption) \\ &= \prod_{i=1}^n p(x_i|y) \end{aligned} p ( x 1 , ⋯ , x n ∣ y ) = p ( x 1 ∣ y ) p ( x 2 ∣ y , x 1 ) ⋯ p ( x n ∣ y , x 1 , ⋯ , x n − 1 ) = p ( x 1 ∣ y ) p ( x 2 ∣ y ) ⋯ p ( x n ∣ y ) ( b y a s s u m p t i o n ) = i = 1 ∏ n p ( x i ∣ y ) 이 가정은 Conditional independence assumption 혹은 Naive Bayes assumption 이라 불린다. 이 가정은 수학적으로 증명된 가정이 아니다.
이 모델의 매개변수들은 다음과 같이 설정한다.
ϕ j ∣ y = 1 = p ( x j = 1 ∣ y = 1 ) ϕ j ∣ y = 0 = p ( x j = 1 ∣ y = 0 ) ϕ y = p ( y = 1 ) \phi_{j|y=1} = p(x_j=1|y=1) \\ \phi_{j|y=0} = p(x_j=1|y=0) \\ \phi_{y} = p(y=1) ϕ j ∣ y = 1 = p ( x j = 1 ∣ y = 1 ) ϕ j ∣ y = 0 = p ( x j = 1 ∣ y = 0 ) ϕ y = p ( y = 1 ) GDA 모델과 유사하게, joint likelihood 를 설정하면,
L ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) = ∏ i = 1 m p ( x ( i ) , y ( i ) ; ϕ y , ϕ j ∣ y ) \mathcal L(\phi_y,\phi_{j|y=0},\phi_{j|y=1}) = \prod_{i=1}^m p(x^{(i)},y^{(i)};\phi_y,\phi_{j|y}) L ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) = i = 1 ∏ m p ( x ( i ) , y ( i ) ; ϕ y , ϕ j ∣ y ) 마찬가지로 MLE를 사용하게 되면,
ϕ y = ∑ i = 1 m 1 { y ( i ) = 1 } m ϕ j ∣ y = 1 = ∑ i = 1 m 1 { x j ( i ) = 1 ∧ y ( i ) = 1 } ∑ i = 1 m 1 { y ( i ) = 1 } ϕ j ∣ y = 0 = ∑ i = 1 m 1 { x j ( i ) = 1 ∧ y ( i ) = 0 } ∑ i = 1 m 1 { y ( i ) = 0 } \phi_y = \frac{\sum_{i=1}^m 1\{y^{(i)}=1\}}{m} \\ \phi_{j|y=1} = \frac{\sum_{i=1}^m 1\{x_j^{(i)}=1 \wedge y^{(i)}=1 \}}{\sum_{i=1}^m 1\{y^{(i)}=1\}} \\ \phi_{j|y=0} = \frac{\sum_{i=1}^m 1\{x_j^{(i)}=1 \wedge y^{(i)}=0 \}}{\sum_{i=1}^m 1\{y^{(i)}=0\}} ϕ y = m ∑ i = 1 m 1 { y ( i ) = 1 } ϕ j ∣ y = 1 = ∑ i = 1 m 1 { y ( i ) = 1 } ∑ i = 1 m 1 { x j ( i ) = 1 ∧ y ( i ) = 1 } ϕ j ∣ y = 0 = ∑ i = 1 m 1 { y ( i ) = 0 } ∑ i = 1 m 1 { x j ( i ) = 1 ∧ y ( i ) = 0 }
How to calculate ? Note :p ( y ) = ϕ y y ( 1 − ϕ y ) 1 − y p ( x ∣ y = 0 ) = ∏ j = 1 n p ( x j ∣ y = 0 ) = ∏ j = 1 n ( ϕ j ∣ y = 0 ) x j ( 1 − ϕ j ∣ y = 0 ) 1 − x j p ( x ∣ y = 1 ) = ∏ j = 1 n p ( x j ∣ y = 1 ) = ∏ j = 1 n ( ϕ j ∣ y = 1 ) x j ( 1 − ϕ j ∣ y = 1 ) 1 − x j \begin{aligned} p(y) &= {\phi_y}^y(1-\phi_y)^{1-y} \\ p(x|y=0) &= \prod_{j=1}^n p(x_j|y=0) \\ &= \prod_{j=1}^n (\phi_{j|y=0})^{x_j}(1-\phi_{j|y=0})^{1-x_j} \\ p(x|y=1) &= \prod_{j=1}^n p(x_j|y=1) \\ &= \prod_{j=1}^n (\phi_{j|y=1})^{x_j}(1-\phi_{j|y=1})^{1-x_j} \end{aligned} p ( y ) p ( x ∣ y = 0 ) p ( x ∣ y = 1 ) = ϕ y y ( 1 − ϕ y ) 1 − y = j = 1 ∏ n p ( x j ∣ y = 0 ) = j = 1 ∏ n ( ϕ j ∣ y = 0 ) x j ( 1 − ϕ j ∣ y = 0 ) 1 − x j = j = 1 ∏ n p ( x j ∣ y = 1 ) = j = 1 ∏ n ( ϕ j ∣ y = 1 ) x j ( 1 − ϕ j ∣ y = 1 ) 1 − x j L e t log L ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) = l ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) Let \space \log \mathcal L(\phi_y,\phi_{j|y=0},\phi_{j|y=1}) = l(\phi_y,\phi_{j|y=0},\phi_{j|y=1}) L e t log L ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) = l ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) φ \varphi φ l ( φ ) = log ∏ i = 1 m ( ∏ j = 1 n p ( x j ( i ) ∣ y ( i ) ; φ ) ) p ( y ( i ) ; φ ) = ∑ i = 1 m ( log p ( y ( i ) ; φ ) + ∑ j = 1 n log p ( x j ( i ) ∣ y ( i ) ; φ ) ) = ∑ i = 1 m { y ( i ) log ϕ y + ( 1 − y ( i ) ) l o g ( 1 − ϕ y ) + ∑ j = 1 n ( x j ( i ) log ϕ j ∣ y ( i ) + ( 1 − x j ( i ) ) log ( 1 − ϕ j ∣ y ( i ) ) ) } \begin{aligned} l(\varphi) &=\log\prod_{i=1}^m \left( \prod_{j=1}^n p({x_j}^{(i)}|y^{(i)};\varphi)\right) p(y^{(i)};\varphi) \\ &= \sum_{i=1}^m \left( \log p(y^{(i)};\varphi)+\sum_{j=1}^n \log p({x_j}^{(i)}|y^{(i)};\varphi) \right) \\ &=\sum_{i=1}^m \{ y^{(i)}\log\phi_y + (1-y^{(i)})log(1-\phi_y) \\ &\qquad +\sum_{j=1}^n ( {x_j}^{(i)}\log\phi_{j|y^{(i)}} +(1-{x_j}^{(i)})\log(1-\phi_{j|y^{(i)}})) \} \end{aligned} l ( φ ) = log i = 1 ∏ m ( j = 1 ∏ n p ( x j ( i ) ∣ y ( i ) ; φ ) ) p ( y ( i ) ; φ ) = i = 1 ∑ m ( log p ( y ( i ) ; φ ) + j = 1 ∑ n log p ( x j ( i ) ∣ y ( i ) ; φ ) ) = i = 1 ∑ m { y ( i ) log ϕ y + ( 1 − y ( i ) ) l o g ( 1 − ϕ y ) + j = 1 ∑ n ( x j ( i ) log ϕ j ∣ y ( i ) + ( 1 − x j ( i ) ) log ( 1 − ϕ j ∣ y ( i ) ) ) } ∇ ϕ j ∣ y = 0 l ( φ ) = ∑ i = 1 m ( x j ( i ) 1 ϕ j ∣ y = 0 1 { y ( i ) = 0 } − ( 1 − x j ( i ) ) 1 1 − ϕ j ∣ y = 0 1 { y ( i ) = 0 } ) \begin{aligned} \nabla_{\phi_{j|y=0}} l(\varphi) &= \sum_{i=1}^m \left( {x_j}^{(i)}\frac{1}{\phi_{j|y=0}}1\{y^{(i)}=0\} - (1-{x_j}^{(i)})\frac{1}{1-\phi_{j|y=0}}1\{y^{(i)}=0\} \right) \end{aligned} ∇ ϕ j ∣ y = 0 l ( φ ) = i = 1 ∑ m ( x j ( i ) ϕ j ∣ y = 0 1 1 { y ( i ) = 0 } − ( 1 − x j ( i ) ) 1 − ϕ j ∣ y = 0 1 1 { y ( i ) = 0 } ) N o t e : ( 1 − ϕ j ∣ y = 0 ) = ϕ j ∣ y = 0 Note :\space(1-\phi_{j|y=0}) = \phi_{j|y=0} N o t e : ( 1 − ϕ j ∣ y = 0 ) = ϕ j ∣ y = 0 ∇ ϕ j ∣ y = 0 l ( φ ) = 0 = ∑ i = 1 m ( ( x j ( i ) − ϕ j ∣ y = 0 ) 1 { y ( i ) = 0 } ) = ∑ i = 1 m ( x j ( i ) 1 { y ( i ) = 0 } ) − ϕ j ∣ y = 0 ∑ i = 1 m 1 { y ( i ) = 0 } = ∑ i = 1 m ( 1 { x j ( i ) = 1 ∧ y ( i ) = 0 } ) − ϕ j ∣ y = 0 ∑ i = 1 m 1 { y ( i ) = 0 } \begin{aligned} \nabla_{\phi_{j|y=0}} l(\varphi) &= 0 \\ &=\sum_{i=1}^m \left( ({x_j}^{(i)}-\phi_{j|y=0})1\{y^{(i)}=0\} \right) \\ &= \sum_{i=1}^m ( {x_j}^{(i)}1\{y^{(i)}=0\})-\phi_{j|y=0}\sum_{i=1}^m1\{y^{(i)}=0\} \\ &= \sum_{i=1}^m (1\{ {x_j}^{(i)}=1\wedge y^{(i)}=0\})-\phi_{j|y=0}\sum_{i=1}^m1\{y^{(i)}=0\} \\ \end{aligned} ∇ ϕ j ∣ y = 0 l ( φ ) = 0 = i = 1 ∑ m ( ( x j ( i ) − ϕ j ∣ y = 0 ) 1 { y ( i ) = 0 } ) = i = 1 ∑ m ( x j ( i ) 1 { y ( i ) = 0 } ) − ϕ j ∣ y = 0 i = 1 ∑ m 1 { y ( i ) = 0 } = i = 1 ∑ m ( 1 { x j ( i ) = 1 ∧ y ( i ) = 0 } ) − ϕ j ∣ y = 0 i = 1 ∑ m 1 { y ( i ) = 0 } ϕ j ∣ y = 1 \phi_{j|y=1} ϕ j ∣ y = 1 ϕ y \phi_y ϕ y ∇ ϕ y l ( φ ) = ∑ i = 1 m ( y ( i ) 1 ϕ y − ( 1 − y ( i ) ) 1 1 − ϕ y ) = ∑ i = 1 m ( y ( i ) ( 1 − ϕ y ) − ( 1 − y ( i ) ) ϕ y ) = ∑ i = 1 m y ( i ) − ∑ i = 1 m ϕ y \begin{aligned} \nabla_{\phi_y}l(\varphi) &= \sum_{i=1}^m \left( y^{(i)}\frac{1}{\phi_y} -(1-y^{(i)})\frac{1}{1-\phi_y} \right) \\ &= \sum_{i=1}^m \left( y^{(i)}(1-\phi_y)-(1-y^{(i)})\phi_y \right) \\ &= \sum_{i=1}^m y^{(i)} - \sum_{i=1}^m \phi_y \end{aligned} ∇ ϕ y l ( φ ) = i = 1 ∑ m ( y ( i ) ϕ y 1 − ( 1 − y ( i ) ) 1 − ϕ y 1 ) = i = 1 ∑ m ( y ( i ) ( 1 − ϕ y ) − ( 1 − y ( i ) ) ϕ y ) = i = 1 ∑ m y ( i ) − i = 1 ∑ m ϕ y
이 모델은 반복전인 작업을 하지 않고 실제로 매우 효율적인 알고리즘이라 할 수 있지만, logistic regression모델을 사용할 경우 거의 항상 더 나은 모습을 보여준다. 하지만, 종종 확률이 0이되는 경우가 문제가 되어 Laplace smoothing을 사용하게 된다.