Lecture 6

Naive Bayes

---

Naive Bayes에서 feature x가 다음과 같은 베르누이 분포가 아닌 $x\in\{1,....,k\}$ 인 Multinomial value를 가질 때, 쉽고 빠르게 일반화가 가능하다. 또한, 입력값이 연속적인 경우에도 이를 부분으로 나누어 이산화 시켜 적용이 가능하다.

feet	< 400	400 - 800	800-1200	1200-1600	>1600
x	1	2	3	4	5

하지만, 이 Naive Bayes 알고리즘은 약간의 문제점이 존재한다.

예를 들어, 사전에 NIPS라는 단어가 6017번째에 있다고 가정한다. 하지만, 보통 이런 단어는 이메일에서 거의 등장하지 않는 단어다. 그렇기에 현재 이메일 데이터 셋을 이용해 매개변수들의 Maximum likelihood estimate를 구한다면 다음과 같다. ( 표현을 조금 간소화 했다. 조금 더 자세한 식은 앞선 강의를 참고하면 된다.)

또한, 최종적으로 구하고자 하는 것은 베이즈 정리에 의해서 다음 수식으로 정의됨을 알고있다.

그런데, 앞서 구한 $\phi_{6017|y=0}$ 과 $\phi_{6017|y=1}$ 모두 0 이므로, $p(y=1|x) = \frac{0}{0+0}$ 이 된다.

0을 0으로 나눈다는 오류와 별개로, 트레이닝 셋에서 한번도 보지 못한 단어가 나올 확률을 0으로 추정하는 것은 꽤 좋지 않은 방식임을 쉽게 알 수 있다.

Laplace smoothing

---

Naive Bayes는 실제로 많은 문제에서 잘 작동하지만, 앞서 말한 문제를 보완하고 조금 더 잘 작동시키기 위해 Laplace smoothing 기법이 나오게 되었다.

이번에는 text classification이 아닌, 어떤 팀의 승률 예측을 예로 한다.

토트넘이 다음과 같은 경기 결과를 얻었을 때, 토트넘이 이길 확률은 다음과 같다.

day	team	win / lose
8/6	사우샘프턴	0
8/15	첼시	0
8/20	울브스	0
9/3	풀럼	0
9/11	맨시티	predict

이와 같이 확률이 너무 극단적으로 가는 것을 방지하기 위해서, Laplace smoothing은 각 win/lose에 대한 경험을 한번 씩 추가하여 계산한다. 즉, 실제로 토트넘은 한번도 이기지 못했지만 1번 이겼다고 가정하며, 실제로 4번 졌지만 5번을 졌다고 가정한다.

$x\in\{1,...,k\}$에 대해 일반화를 시키면 , Maximum likelihood estimates는 다음과 같게 됨을 쉽게 알 수 있다.

또한 같은 방법으로, Naive Bayes에 Laplace smoothing을 적용하면, 매개변수들의 estimates는 다음과 같다.

Event models for text classification

---

Naive Bayes에서 사용하던 feature x의 표현은 다음과 같았다.

이때, 이메일에 “Drugs! Buy Drugs now!”라는 문장을 확인할 때 Naive Bayes 알고리즘은 Drugs 라는 단어가 두번 나왔다는 정보를 확인하지 않는다. 이런 모델을 Multivariate Bernoulli event model이라 부른다.

이러한 점을 보완해서 만든 모델을 Multinomial event model로 부른다. 이메일에 대해 다음과 같은 새로운 feature x를 생각할 수 있다. ($n_i$는 이메일 i의 길이에 해당한다.)

이 모델의 likelihood는 Navie Bayes assumption을 사용하면 다음과 같이 주어진다.

이는 앞에서 나왔던 Multivariate Bernoulli event model의 Likelihood와 모양이 같아 혼란이 있을 수 있지만, $x_j와 n_i$의 정의가 다름을 알아야 한다.

Maximum likelihood estimates을 사용하여 매개변수들을 구하면,

말로 풀어쓰면 $\phi_{k|y=0} = p(x_j=k|y=0)=Chance\space of\space word\space j\space being\space k\space if \space y=0$ 가 된다. 여기서는 이 확률이 j, 즉 단어의 위치와 관련 없다. ($x_j$는 이메일에서 j번째 단어를 말한다.)

이 식에 Laplace smoothing을 적용하면,

하지만, 사전에 모든 단어를 담을 수 없다. 사전에 없는 단어가 등장하게 되면 두 가지 방식을 사용할 수 있다. 이에 관한 자세한 내용은 다루지 않는다.

1. 그 단어를 없는 취급한다
2. 거의 등장하지 않는 단어들을 UNK라는 토큰에 대체하는 방법이 존재한다.

Naive Bayes의 장점은 계산이 매우 효율적이고, 구현이 빠르며, 반복적인 경사 하강법이 필요하지 않다는 것이다. 하지만, 대부분의 문제들을 푸는데 있어 Naive Bayes 알고리즘에 비해 Logistic regression이 조금 더 나은 정확성을 제공하고 잘 작동한다는 것이 알려져있다.

Part 5 Support Vector Machines

---

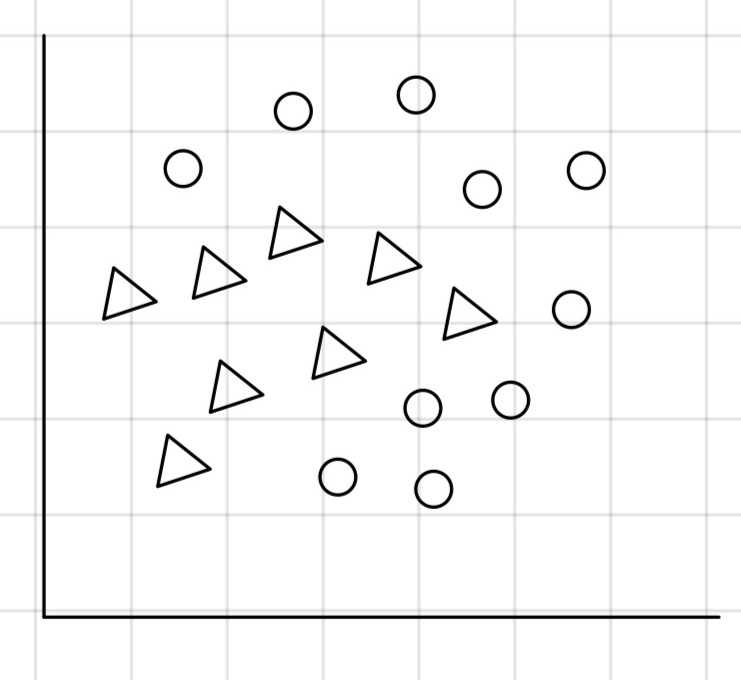
다음과 같은 비선형 결정경계를 선태해야 하는 상황에서 Gaussian Discriminant Analysis는 직선 결정 경계를 선택할 것이다.

Logistic regression에서는 feature 벡터 $x_1, x_2$를 더 높은 차원에 대응시킨 새로운 feature 벡터 $\phi_x$를 직접 선택하고 적용시킨 다면, 비선형 결정경계를 학습하여 얻어 낼 수 있다.

하지만, 이런 방식은 너무 어렵고 경계가 단순한 도형이 아니라면 더욱 더 복잡하다.

Support Vector Machine에서는 feature $x_1,x_2$를 더 높은 차원의 featrue set으로 매핑하는 알고리즘을 도출하고, Linear Classifier을 적용한다. 이는 Logistic regression의 방식과 유사하지만, 세부적으로 비선형 결정경계를 학습하는 방법이 다르다.

오늘날 SVM이 후에 배울 neural newtworks에 비해 효과적이지 않지만, 사용되는 이유 중 하나는 turn-key의 속성을 가진 알고리즘이기 때문이다. 즉, 조작하는 매개변수의 양이 상대적으로 적다.

Margins: Intuition

---

먼저, Margin에 대해 이해해야 한다. 다음 그림과 같은 데이터 셋이 존재하고 Logistic regression을 사용하면, 검은 선이 그려지게 될 것이다.

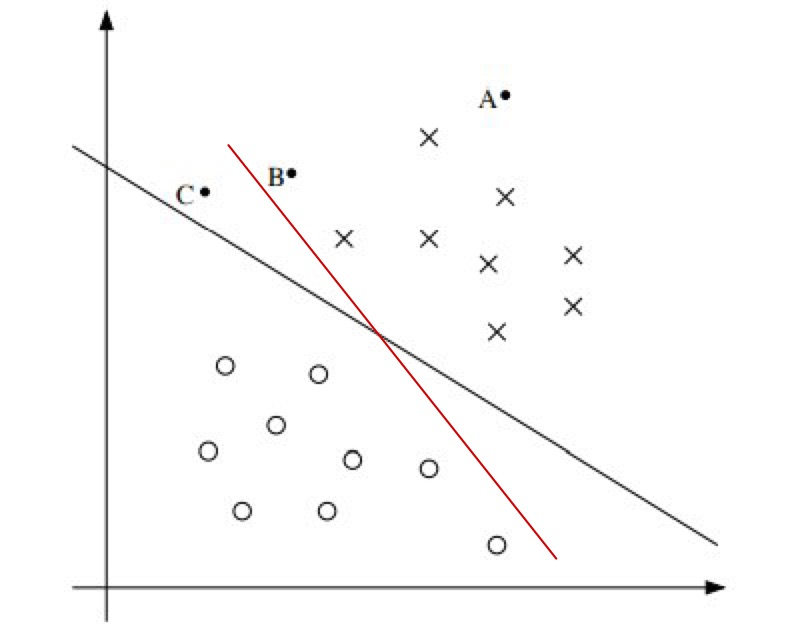
그림의 결정 경계는 Seperating hyperplane으로 불린다.

알다시피, Logistic regression은 $h_\theta(x) = g(\theta^Tx)$로 만약 $\theta^Tx \leq 0$ 이라면 $y =0$ 으로 예측한다. 반대로, $\theta^Tx \geq 0$ 이라면 $y=1$으로 예측하게 된다.

바꿔 말하면, $y^{(i)}=1$ 이라면 Sigmoid function의 모양에 의해 $\theta^Tx \gg 0$ 이어야 confident prediction을 할 수 있다.

그렇기에 왼쪽 그림에서 빨간 선 보다 검은 선을 더 좋은 결정경계라 판단하는 근거가 된다.

A,B,C 세개의 점에 대한 y의 값을 판별 할 경우 A점에 대해 가장 강하고 정확한 예측이 가능하다.

Notation

---

SVM에서는 새로운 표기법을 사용한다. 기존의 $y\in\{0,1\}$과 $h_\theta(x) = g(\theta^Tx)$에서 다음과 같이 표기한다.

$x_0$는 1로 생각하지 않는다.

Functional and geometric margins

---

앞서 정한 표기법과 margin을 최대화 시키고자 하는 것을 이용해 다음 $\hat{\gamma}^{(i)}$를 매개변수 w와 b로 정의할 수 있다. 이를 Functional margin of hyperplane이라 한다. 표기는 다음과 같다.

$\hat{\gamma}^{(i)}$의 값이 0보다 클수록 알고리즘이 정확하고 confident한 예측을 할 수 있음을 말한다.

이제 전체 트레이닝 예제에 대해서 다음을 정의한다.

이는 가장 안좋은 예제에서 이 알고리즘이 얼마나 잘 수행하는지 확인 할 수 있는 값이다.

Functional margin의 특징 중 하나는 매개변수의 값을 손쉽게 조절이 가능하다는 점이다. 가령, (w,b)에서 (2w,2b)로 바꾸어도 결정경계는 변하지 않는다. 이를 이용해 매개변수 w,b 를 normalize가 가능하다.

다음 그림에서 $\gamma^{(i)}$의 값을 구해보면,

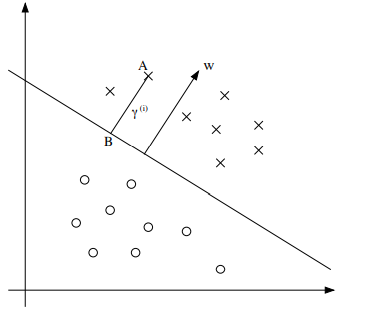
직선은 $w^Tx+b= 0$을 나타낸다.

따라서 직선과 수직인 벡터는 $w$가 되고 이때, $\frac{w}{\lVert w \rVert}$는 수직벡터의 방향을 나타낸다.

현재 A는 벡터 $x^{(i)}$에 위치해있으므로, B지점의 x좌표는 쉽게 구할 수 있다.

위의 식에서 $\gamma^{(i)}$로 정리하면,

그리고 Geometric Margin은 다음과 같이 정의가 된다. ( $y^{(i)} = 1 \text{ or } -1$이므로 다음 식이 성립한다.)

앞서 functional margin과 마찬가지로 geometric margin에 대해 다음을 정의한다.