Lecture 7
The optimal margin classifier
maximizing (geometric margin)
SVM의 목적은 margin을 최대화 하는 것이기 때문에 다음과 같이 식을 쓸 수 있다.
💡 training set 은 선형적으로 분리되어 있다는 가정을 해야 한다. 즉, hyperplane을 이용해 양과 음의 예제들로 완벽하게 분리가 가능하다는 가정이다.optimization problem
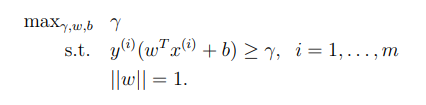
는 functional margin 과 geometric margin이 똑같게 해주는 식이다. 위의 optimization problem을 풀게되면 의 최대값을 구할 수 있다. 하지만 이 볼록하지 않기 때문에 공식을 사용하기에 불편하다. 따라서 식을 변경하면,
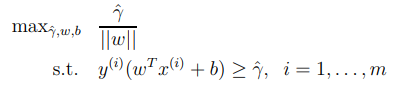
그라나 아직 도 공식을 사용하기엔 불편하므로 다음과 같이 변경 할 수 있다.
와 는 어떠한 값을 곱해도 선형 경계는 변하지 않는다는 것을 알고 있다(e.x 10와 10를 사용하여도 선형경계는 변하지 않는다.) 따라서 매개변수 와 를 조정하여 이 되게 하여 위의 공식을 변형 시켜보자.
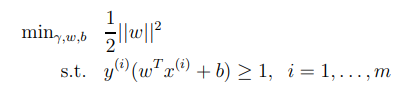
Lagrange duality
💡 Lagrange duality는 optimization problem과는 다른 얘기지만 우리가 optimization problem의 dual form(쌍대형)을 만들어내는데 꼭 필요하다. dual form은 앞으로 나올 내용인 kernel을 사용해 문제를 효율적으로 풀어내는데 꼭 필요한 형태이다.- 다음과 같은 형태의 문제가 있다고 생각해보자
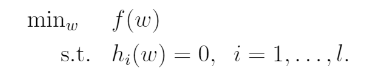
- 즉 의 최솟값을 제약식 을 사용하여 풀어내는 문제이다. 우리는 위의 문제를 Lagrangian form 으로 변경할 수 있다.
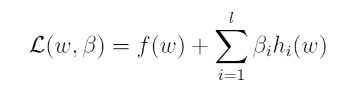
- 여기서 는 Lagrange multipliers 이다.
- 만약 가 KKT(Karush-kuhn-Trucker) 조건을 따른다면, 위의 식은 dual problem의 답을 찾을 수 있다.
- KKT(Karush-kuhn-Trucker) 조건이란
- KKT(Karush-kuhn-Trucker) 조건이란
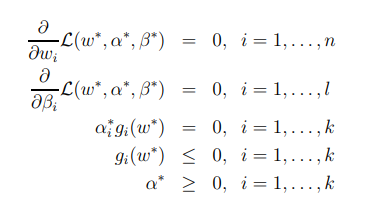
- KKT 조건에서는 은 을 각각의 매개변수로 편미분해서 0이 되는 지점에서 최솟값을 갖는다.
Optimal margin classifiers
Dual optimization problem
우리가 이전에 살펴보았던 optimization problem은 다음과 같다.
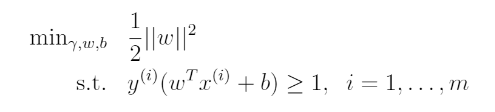
위의 제약식을 다른 방식으로 쓰면 다음과 같다.
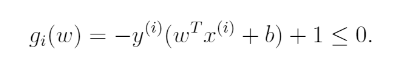
위에서 살펴보았던 Lagrangian을 우리의 optimization problem 에 적용시키면 다음과 같이 된다.
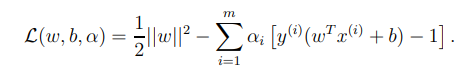
을 각각의 매개변수로 편미분해서 0이 되는 지점에서 최솟값이 되므로 다음의 과정을 거쳐 dual optimization problem을 도출 할 수 있다.
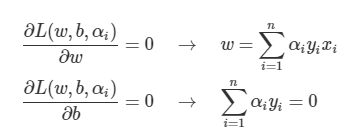
위의 식을 원래의 optimization problem 에 대입하면 다음과 같은 식이 나온다.
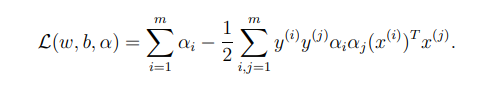
계산과정은 아래의 내요을 참고하면 된다.
- 첫번째 항
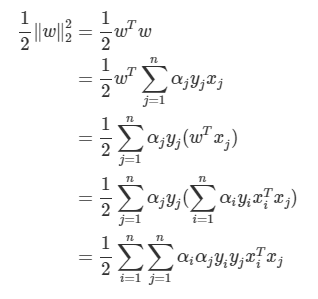
- 두번째 항
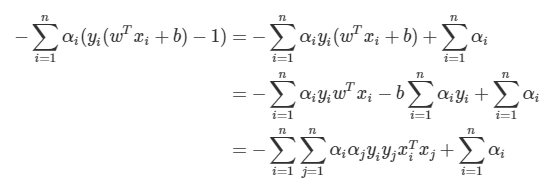
우리는 의 값을 최소화 하는 것이 목표이기 때문에 제약식과 함께 공식을 써보면
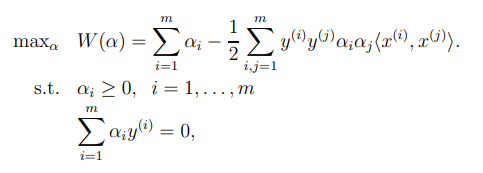
우리는 이렇게 KKT조건 하에, Lagrange duality를 사용하여 dual problem을 primal problem 형태로 풀 수 있게 된 것이다.
SVM의 해
우리가 최종적으로 찾고자 하는 것은 margin이 최대화된 분류 경계면 이다. 즉 와 를 찾으면 분류 경계면을 찾을 수 있는 것 이다. 위의 식에서 파생된 를 확인해 보자.
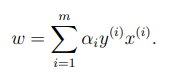
만약 이라면 이러한 관측치는 결정 경계를 만드는 데 아무런 영향을 끼치지 못한다. 즉 이여야 margin 결정에 유의미 하다.
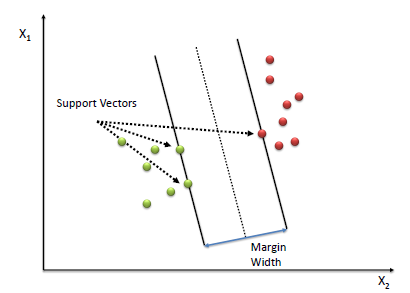
위의 그림에서 결정 경계와 가장 가까운 점은 3개 인 것을 확인 할 수 있다. 이 3개의 점은 모두 결정 경계와 평행한 선에 위치해 있다. 이렇게 margin 결정에 영향을 끼치는 점들을 support vector(서포트 벡터) 라고 부른다.
이때, 은 다음과 같이 쓸 수 있다.
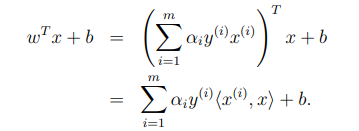
Kernel
Why we use Kernel SVM?
일반적으로 SVM은 두 범주를 잘 분류하면서 margin이 최대화된 hyperplane을 찾는 방법이다.
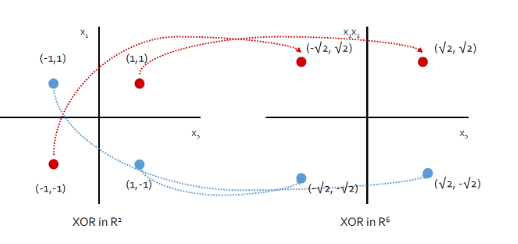
그러나 만약 두 범주가 선형으로 잘 분리되지 않는다면 어떻게 될까? 다음의 예제를 살펴보자.
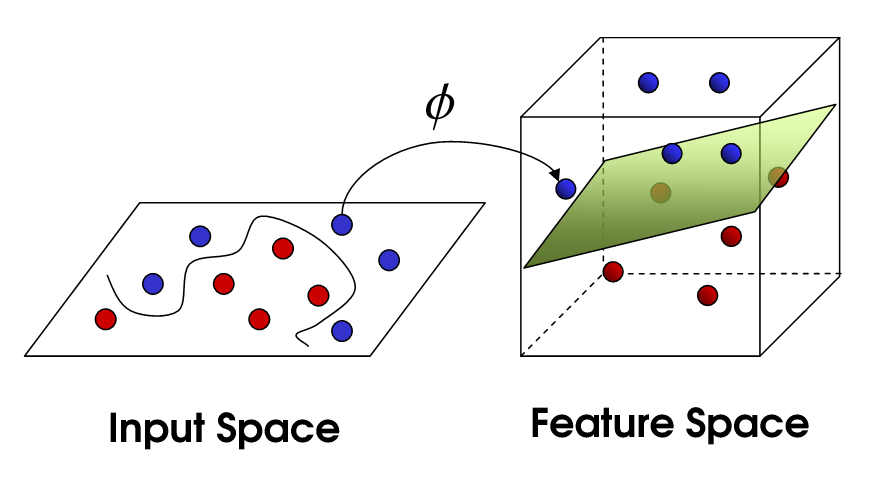
위의 input space의 예제를 보면 선형적으로 구분할 수 없는 input 값들이 보인다. 하지만 이 데이터를 고차원 평면(feature space)으로 mapping한뒤 분류하면, 두 범주를 분류할 수 있는 hyperplane을 찾을 수 있다. 우리는 이러한 방법을 kernel SVM 이라고 한다.
Kernel SVM
how to make kernel?
- Write algorithm in terms of
- Let there be mapping from →
- Find way to xompute
- Replace in algorithm with
mapping function
kernel trick에서 가장 중요한것은 input space와 feature space를 연결 시켜주는 mapping function이다. 예를들어 다음과 같은 예제를 통해 알아보자
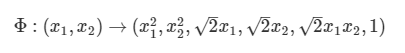
원래의 는 2차원의 벡터였지만 mapping function 를 통해 6차원의 벡터로 변환시킨다. 이렇게 변환시킨 데이터를 살펴보면 다음과 같이 선형으로 분리가 불가능 했던 데이터가 선형으로 분리가 가능하게 된다.
이전 SVM은 input space의 값을 적용했다면 kernel SVM은 input space의 값들이 mapping function으로 변환된 feature 데이터들을 적용한다. 그렇게 하려면 SVM 알고리즘에서의 모든 값들을 의 값들로 변환시켜주면 된다.
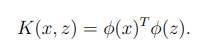
Kernel trick
💡 흥미로운 점은 $K(x,z)$는 고차원의 데이터를 다루어야 해서 매우 expensive 할 것 같지만 실제로는 그렇지 않다. 바로 kernel trick이 있기 때문이다.가 차원의 값이라고 가정할 때 하나의 예시를 살펴보자
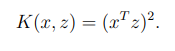
이것은 다음과 같이 쓰여질 수 있다.
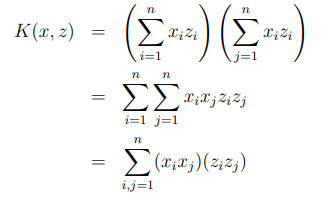
이므로 n=3일때 는 다음과 같은 형태가 된다.
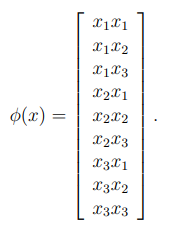
여기서 알 수 있듯이, 고차원의 를 계산하는데 의 시간이 걸리지만, 를 찾는데는 의 시간이 걸린다.