Lecture 8

Bias and variance

---

데이터셋에 어떤한 Bias가 있는지, 어떠한 variance가 있는지 알아보고 학습 알고리즘을 개선한다.

Bias and variance in linear regression

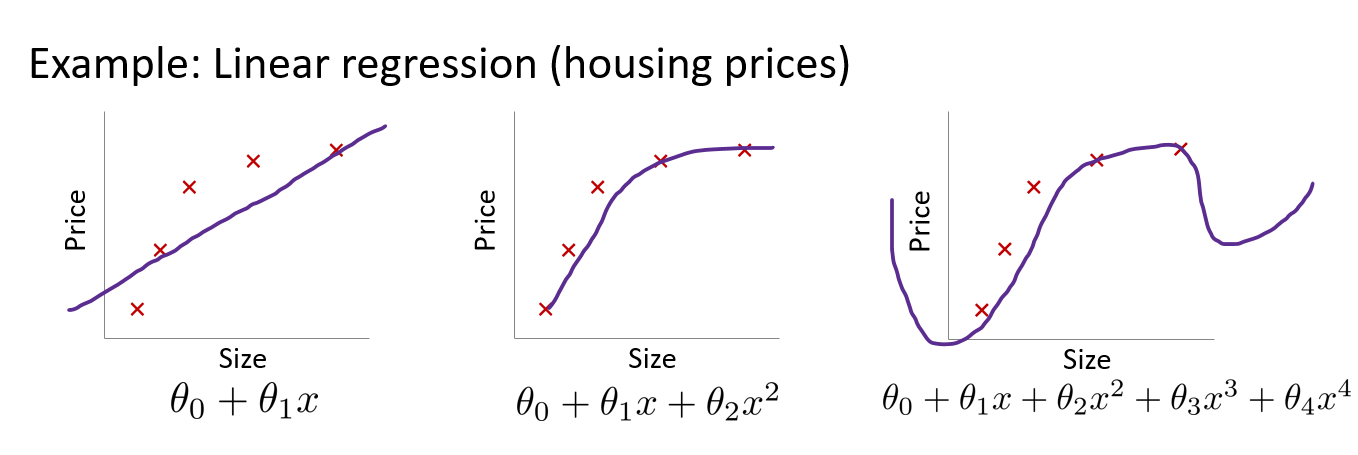
Underfitting, high bias

1. 집의 가격과 집의 크기 사이의 관계가 선형적이라는 강한 편견)
2. 예측값과 실제 정답과의 차이가 크다.

Just fit

Overfitting, high variance

1. 예측값이 정답과 유사하므로, bias는 작다.
2. 그러나 모델의 예측값이 다양하므로 편차가 크다, variance 가 크다.

Bias and variance in classification

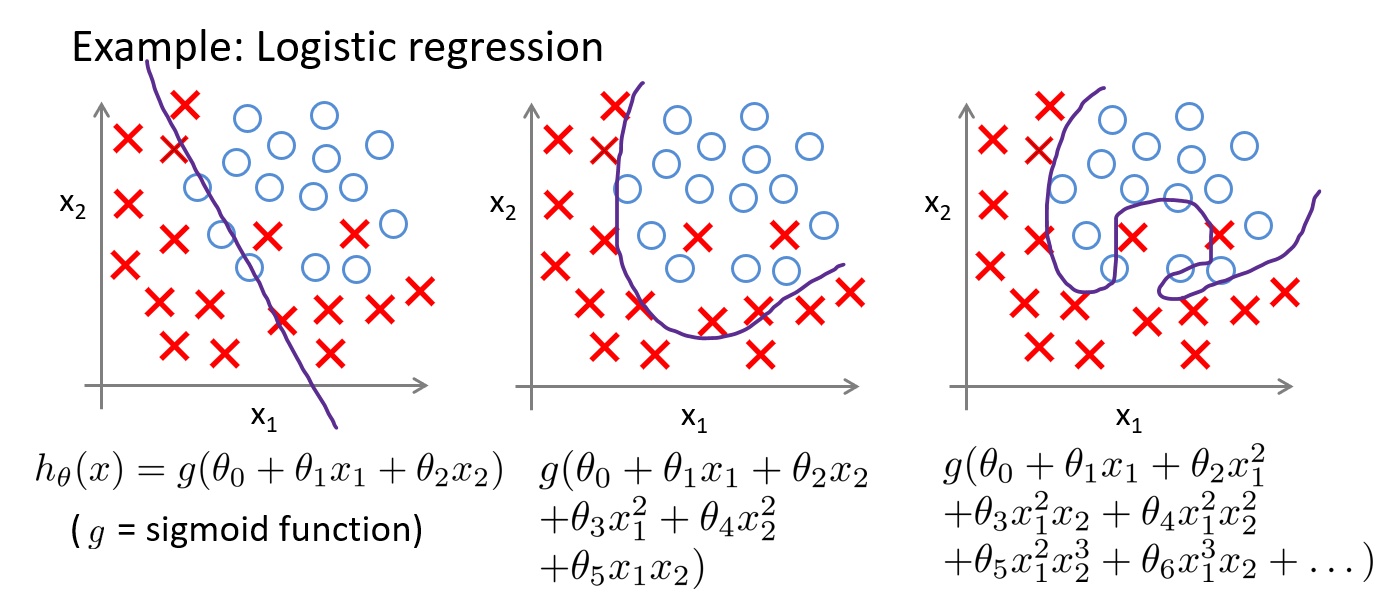
Underfitting

Just fit

Overfitting

Regularization

---

One of the most effective ways to prevent overfitting

Optimization objective for linear regression : $min{1 \over 2}\sum_{i=0}^{m}||y^i-\theta^Tx^i||^2$

→ 여기서 정규화를 추가하면 $min{1 \over 2}\sum_{i=0}^{m}||y^i-\theta^Tx^i||^2+{1 \over 2}\lambda||\theta||^2$

In logistic regression: $argmax \sum_{i=1}^{m}logP(y^i|x^i;\theta)-\lambda||\theta||^2$

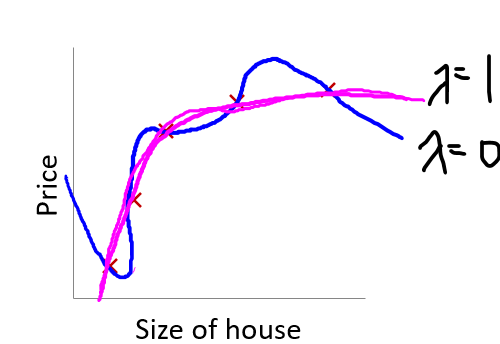
• 람다가 0일 때는 데이터셋에 딱 맞아 overfitting이 생긴다.
• 람다가 적절한 값일 때는 Just fit 이라고 할 수 있다.
• 람다가 너무 큰 값을 가질 때는 underfitting이 생긴다.
• 람다가 $10^{100}$과 같이 매우 큰 값을 가질 때는 함수가 h(x)가 0을 가리킨다.

정규화가 진행되는 간략한 과정

$S=[{x^i,y^i}]_{i=1}^{m}$ 라고 할 때, $p(\theta|S)={p(S|\theta)\times p(\theta) \over p(s)}$라고 할 수 있다. (by bayes rule)

$argmax P(\theta|S)=argmax{P(S|\theta)\times p(\theta)} = argmax(\prod_{i=1}^{m}P(y^i|x^i,\theta)P(\theta))$

P가 가우시안 분포를 따른다고 가정할 때, $P(\theta)$를 구할 수 있다.

→이러한 과정을 거친 후에 컴퓨터 과정을 거쳐 정규화를 할 수 있다.

Generalization Error

머신러닝의 목표는 학습데이터에 대해 잘 작동하는 것이 아닌 새로운, 보지 못 했던 데이터에 대해 잘 작동하는 것

관측하지 못한 데이터에 대해 잘 작동하는 능력을 “generalization “

보통 overfitting 한 경우, 새로운 데이터 셋에 대하여 적응하지 못해 Error 가 올라간다.

→ 이를 generalization error라고 한다.

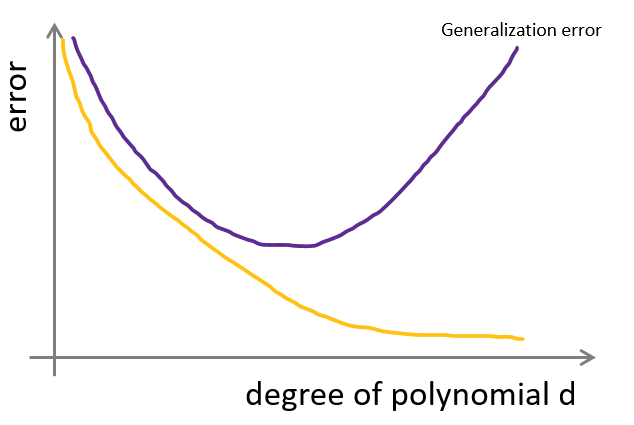
그래프의 좌측에서는 underfitting 하고 중앙에서는 fitting하고 우측에서는 overfitting 하다. 보통 그래프의 차수가 올라갈수록 train data에 대해서는 error가 낮아진다. 그러나 새로운 데이터가 들어왔을 때,
적응하지 못해 error가 올라간다.

Data Splits

Generalization error를 줄이기 위해 data split을 사용한다.

데이터셋을 하위 집합으로 분할하는 것으로부터 시작한다. (train, dev, test sets)

$S_{train}, S_{dev},S_{test}$

데이터 셋이 있고, h(x)를 찾기 위한 모델을 차수별(polynomial)로 다양하게 준비하고

1. 각각의 모델을 train set에서 학습하고, h(x)를 얻을 수 있다.
2. 각각의 error를 development set에서 구하고, 가장 적은 error를 가진 모델을 선택한다.

일반적으로 data set을 (70% train, 30% test ), (60% train, 20% dev, 20% test) 와 같은 방식으로 구성한다.

Cross Validation

Overfitting을 해결하기 위한 방법이다, Data split 은 Hold-out cross validation이다.

development set = “Cross validation set”

In small datasets:

100개의 data가 있다고 가정할 때, train set에 70개, test set에 30개의 데이터를 가지도록 분할한다.

단점: model을 test하기 위한 데이터가 너무 적다.

→ K fold cross validation이 등장

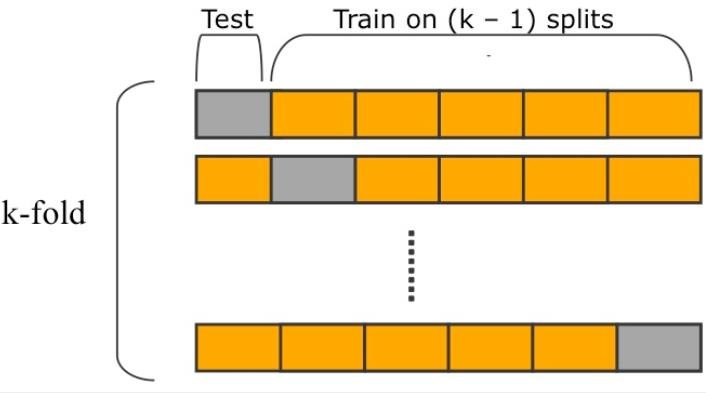
K fold cross validation

데이터 셋을 k개로 나눠서 학습하는 방법 (k=10이 일반적이다.)

k=5일 때, 4번 학습하고 1번은 테스트한다.

ex) (train 1234, test 5) , (train 1245, test 3)

다양한 차수의 함수에 대해 실험한 후, 각각의 실험에서 가장 error 가 적은 경우를 선택한다.

error는 실험에서 평균치를 내서 결정한다.

마지막으로 가장 error가 적은 경우의 모델을 고른 후, 전체 데이터 셋을 대상으로 재 학습을 한다.

K fold c.v의 장점: hold out에서 30퍼센트의 데이터를 test로 씀으로서 데이터를 생략하는 대신 데이터의 1/k 만큼만 생략한다.

k fold c.v의 단점: k회만큼의 iteration이 생긴다.

leave-one-out cross validation

극단적인 버전의 K fold c.v: 데이터셋의 크기가 더 극적으로 적을 때 사용한다.

이 때의 k=데이터셋의 크기

데이터 셋의 크기만큼 반복해야 하기 때문에 expensive한 방법이라고 할 수 있다.

k<100 인 경우가 아니면 거의 사용하지 않는다.

Feature Selection

---

Feature 가 굉장히 많을 때, 그러나 소수의 feature만이 학습에 관련이 있다고 의심이 될때

feature를 고르는 것은 중요하다.

Foward Search: 빈 feature set로부터 시작해서 feature 를 하나씩 추가하는 방법

1단계:

1. script f = 비어있는 feature set
2. 반복적으로 f에 feature들을 추가하려고 한다.
3. 여기서 어떠한 feature이 dev set의 성능을 향상시키는지 확인한다.

2단계:

1. f에 성능을 향상시키는 feature를 추가한다.

ex)

$[x_1,x_2,...x_5]$라는 feature가 있을 때,

1. empty feature set을 대상으로 학습하면 $h(x)=\theta_0$
2. 각각의 feature를 가져와 empty feature set에 추가한다.
3. 어떤 모델이 dev set에서 가장 성능을 잘 향상시키는지 확인해야한다. feature 2를 추가하는 것이 제일 좋다고 가정하자.
4. feature set ={feature2}
5. 2단계로 돌아가 다른 feature들을 추가한다.