[miniRT] #10 평면 구현 [추가]

sham·2022년 3월 31일

[miniRT]

목록 보기

10/19

실습에는 평면을 구현하는 부분이 없었기에 기존 코드, 구조체에 평면에 대한 함수를 추가하였다. ~~드디어 실습 자료를 벗어났다...!~~

추가된 코드

structures.h

struct s_plane
{
	t_point3    center; // 평면의 어느 한 지점.
	t_vec3      dir; // 평면이 가리키는 방향, 어떻게 기울여져 있는지
};

평면에 대한 정보를 담을 구조체를 만들어준다. 평면은 특정 지점에서 특정 벡터를 바라보며 무한히 뻗어나가는 형태이기에 범위는 존재하지 않는다.

hit.c

#include "trace.h"

t_bool hit(t_object *world, t_ray *ray, t_hit_record *rec)
{
    t_bool  hit_anything;
    t_hit_record *temp_rec;

    temp_rec = rec;
    hit_anything = FALSE;
    while (world) // world->next로 훑어가며 등록된 구조체를 전부 체크함
    {
        if (hit_obj(world, ray, temp_rec))
        {
            hit_anything = TRUE;
            temp_rec->tmax = temp_rec->t;
            rec = temp_rec;
        }
        world = world->next;
    }

    return (hit_anything);
}

t_bool hit_obj(t_object *world, t_ray *ray, t_hit_record *rec)
{
    t_bool hit_result;

    hit_result = FALSE;
    if (world->type == SP)
        hit_result = hit_sphere(world, ray, rec);
    else if (world->type == PL)
        hit_result = hit_plane(world, ray, rec);
    else if (world->type == CY)
        hit_result = hit_cylinder(world, ray, rec);
    return (hit_result);
}

도형에 따라 다른 충돌 체크 식이 들어가므로 조건문으로 분기를 걸어주자.

hit_plane.c

#include "structures.h"
#include "utils.h"
#include "trace.h"

t_bool	hit_plane(t_object *pl_obj, t_ray *ray, t_hit_record *rec)
{
	t_plane	*pl;
	float	numrator;
	float	denominator;
	float	root;

	pl = pl_obj->element;
	denominator = vdot(ray->dir, pl->dir);
	if (fabs(denominator) < EPSILON)
		return (FALSE);
	numrator = vdot(vminus(pl->center, ray->origin), pl->dir);
	root = numrator / denominator;
	if (root < rec->tmin || rec->tmax < root)
		return (FALSE);
	rec->t = root;
	rec->p = ray_at(ray, root);
	rec->normal = pl->dir;
	set_face_normal(ray, rec);
	rec->color = pl_obj->color;
	return (TRUE);
}

공식

수직인 벡터끼리의 내적 결과는 0

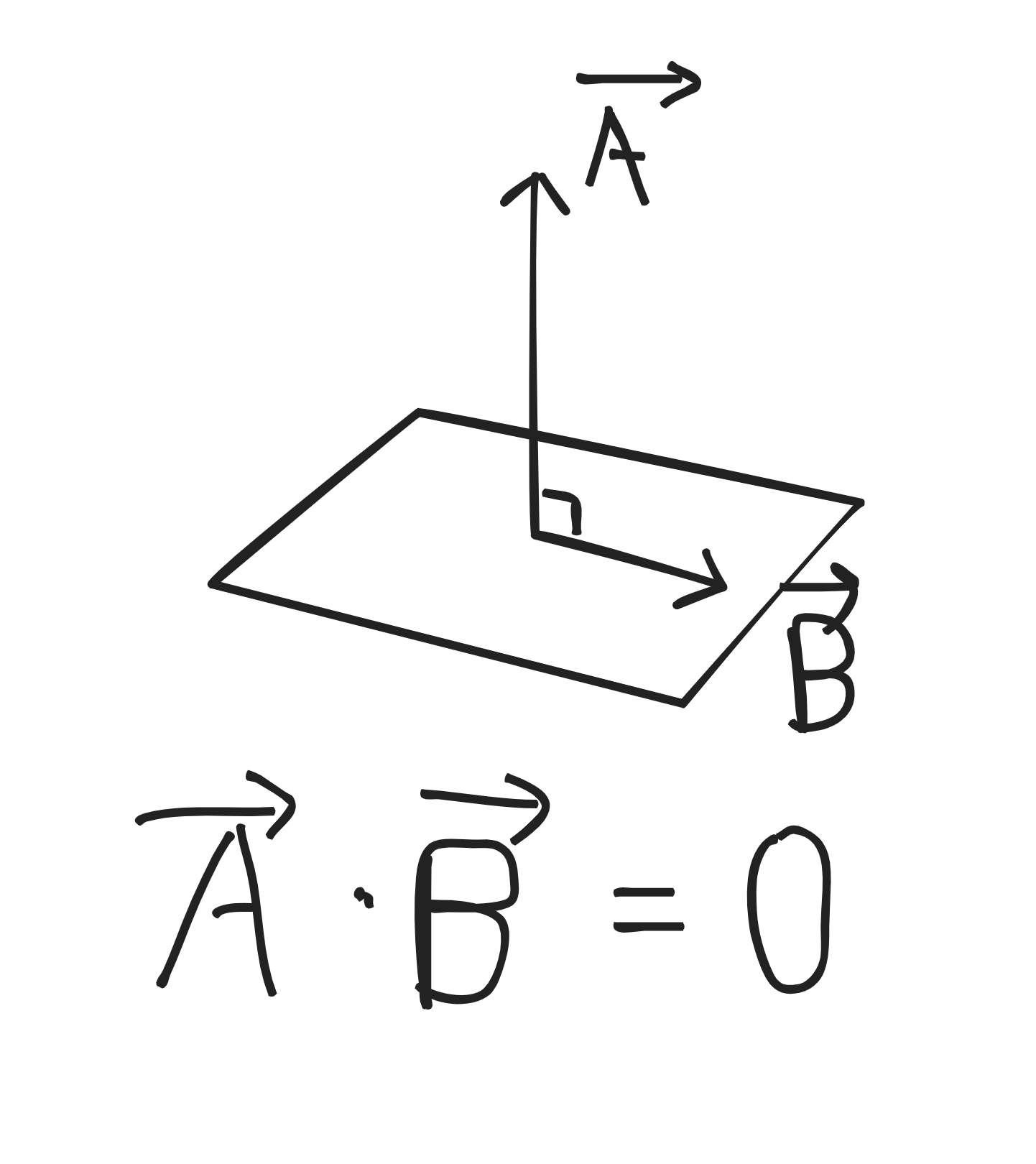
벡터의 내적이 또 등장한다. 서로 수직인 벡터를 내적하면 결과값이 0이 나온다는데, 생각해보면 당연한 결과다. 내적의 뜻은 어떤 벡터가 다른 벡터의 방향에 얼마만큼 도움을 주었는가 라고 말할 수도 있는데, 서로 수직이라면 그 어떤 도움도 주지 않았지만 방해도 주지 않았기에 0이라는 값이 나올 수 있는 것이다.

출처 : [https://ansohxxn.github.io/c++ games/chapter3-2-2/](https://ansohxxn.github.io/c++%20games/chapter3-2-2/)

출처 : https://ansohxxn.github.io/c++ games/chapter3-2-2/

판별식을 이용한 충돌 공식

이제 다시 한 번 사진을 보자.

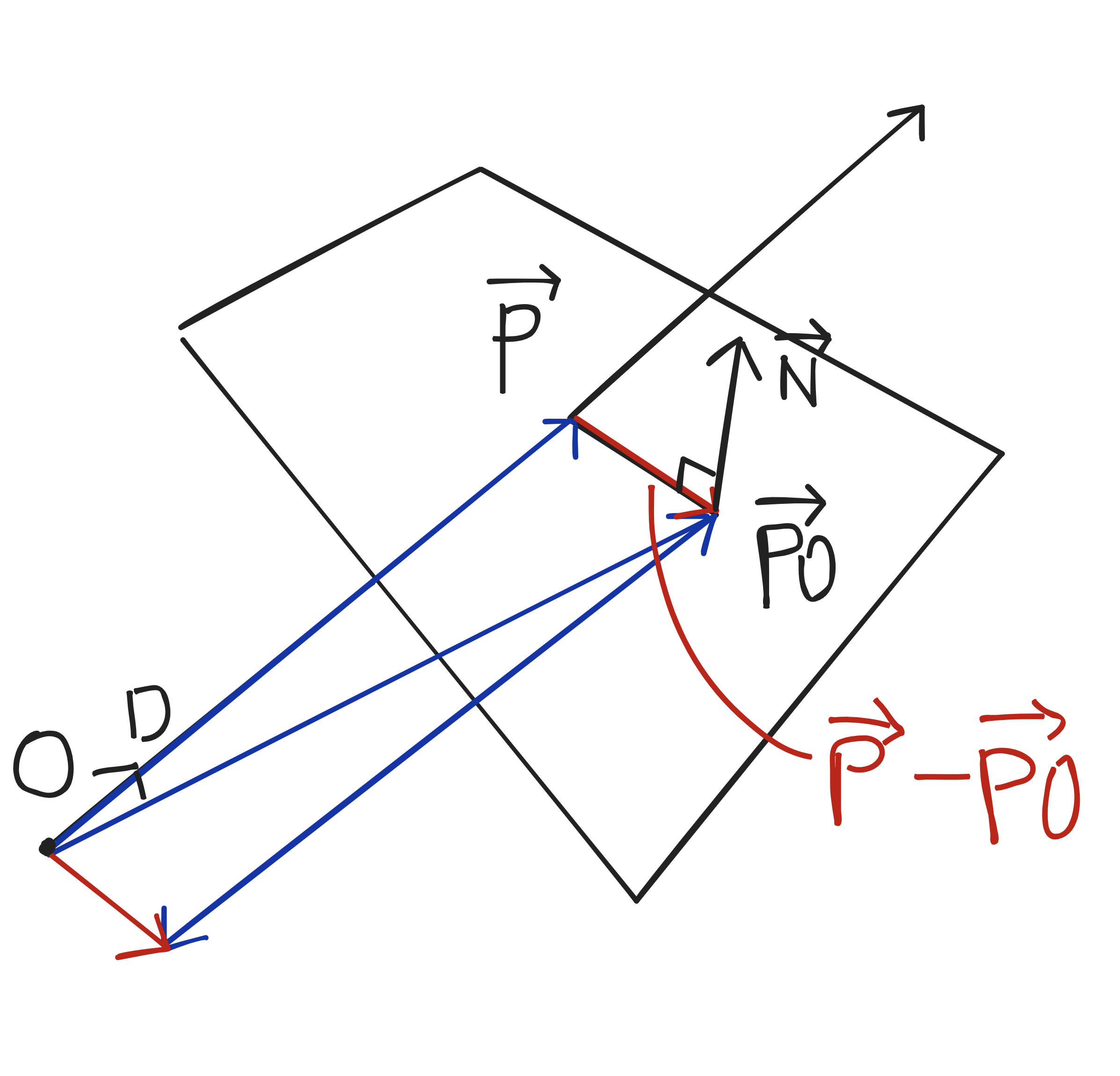
벡터 P는 카메라에서 출발한 임의의 광선이다.

벡터 P0는 인자로 제공되는 평면 상에 어딘가에 존재하는 점이다. 평면의 일부분이라고 할 수 있다.

벡터 N은 인자로 제공되는 평면의 방향 벡터이다. 이 방향 벡터의 수직으로 평면은 뻗어나가고 있다.

바로 위에서 언급했던 것처럼 서로 수직인 두 벡터를 내적하면 0이 나온다는 사실을 우리는 알고 있다.

벡터 N과 수직인 벡터라고 함은 평면의 일부분인 P0과 평면을 지나고 있는 점 P를 이은 벡터, 벡터 P - 벡터 P0이라고 할 수 있을 것이다.

이를 수식으로 표현한다면 다음과 같다.

(\vec P - \vec P_0) \cdot \vec N = 0

이 수식을 전개하면 다음과 같아진다.

(O + \vec D * t - \vec P_0) \cdot \vec N = 0

t(\vec D \cdot \vec N) + (O - \vec P_0) \cdot \vec N = 0

O는 원점, 벡터 D는 벡터 P의 단위 벡터, t는 P까지의 거리(스칼라)이다!

이 수식을 거리인 t에 대한 식으로 전개하면 다음과 같다.

t(\vec D \cdot \vec N)= -(O - \vec P_0) \cdot \vec N

t = { -(O - \vec P_0) \cdot \vec N\over \vec D \cdot \vec N}= { (\vec P_0 - O) \cdot \vec N\over \vec D \cdot \vec N}

위의 식이 판별식이 되어 t가 음수라면 해당 광선, 벡터 P는 평면과 만나지 않는 벡터가 된다.

평면의 벡터가 카메라의 벡터와 반대편일 경우에도 충돌이라고 판정을 해주어야 한다. 판별식의 조건을 절대값으로 체크하자.

코드로 구현할 경우

t_bool      hit_plane(t_object *pl_obj, t_ray *ray, t_hit_record *rec)
{
    t_plane *pl = pl_obj->element;
    float numrator; // 판별식의 분자
    float denominator; // 판별식의 분모
    float root;
    denominator = vdot(ray->dir, pl->normal);
    if (denominator < EPSILON) // 분모의 값이 0보다 작거나 같을 경우 충돌하지 않는다.
        return (FALSE);
    numrator = vdot(vminus(pl->point, ray->orig), pl->normal);
    root = numrator / denominator;
    if (root < rec->tmin || rec->tmax < root) 
        return (FALSE);
    rec->t = root;
    rec->p = ray_at(ray, root);    
    // rec->normal = pl->normal;
    rec->albedo = pl_obj->albedo;
    // print_vec(normal);
    return (TRUE);
}