역시나 실습 자료를 기반으로 진행하였다.
레이 트레이싱

광원으로부터 출발한 (1, 1, 1)의 백색광이 반사율(=albedo)(0.7, 0, 0)인 구에 반사되어 우리 눈에 들어온다면, (1, 1, 1) 중 G와 B에 해당하는 1은 구에 흡수될 것이고 R에 해당하는 1 중 70퍼센트만 반사되어 우리 눈에 들어올 것이다.
백색광(1, 1, 1)이 하나 더 있다면, 교점에 들어오는 광량은 (2, 2, 2)이 될 것이고 오브젝트는 (1.4, 0, 0)를 반사할 것이다(RGB값을 [0, 1]로 매핑했으므로 1을 초과하는 값은 1이 되겠지만 말이다).
반대로 공간 안에 광원이 하나도 없다면 오브젝트는 반사할 빛이 없으므로 검은색일 것이다(밤에 불꺼진 방에서 아무것도 보이지 않듯이).
광원의 개수 말고도 오브젝트 사이의 거리, 물체의 표면, 정반사 난반사 여부 등 다양한 외부 조건에 따라 빛에 대한 반사가 달라지는데, 이 모든 조건을 전부 고려하는 렌더링 기법이 ray tracing이다.
퐁 조명 모델
이론적인 부분은 퐁 조명 모델를 참조.
광원 구현
3차원 벡터 상에서 광원이 위치할 때, 가지게 되는 정보는 총 3가지다.
해당 광원이 위치한 좌표, 해당 광원의 세기, 광원의 색깔.
빛 구조체는 코드 상에서 다음과 같이 설정한다.
structures.h
struct s_light
{
t_point3 origin; // 빛이 위치하는 좌표.
t_color3 light_color; // 빛의 색깔
double bright_ratio;
};이제 광선을 쏘아서 픽셀의 색깔을 정할 때 실제 물체의 색깔 + 명암 처리를 진행한 결과를 토대로 정하게 될 것이다. phong_lighting 함수가 그 빛의 결과를 정하는 함수가 될 것이다. 하나하나 추가해보자.
ray.c
//광선이 최종적으로 얻게된 픽셀의 색상 값을 리턴.
t_color3 ray_color(t_scene *scene)
{
double t;
// t_vec3 n;
scene->rec = record_init();
if (hit(scene->world, &scene->ray, &scene->rec)) // 모든 구조체에 대한 정보를 담은 연결리스트 world로 광선과의 충돌을 테스트한다.
return (phong_lighting(scene)); // 법선 벡터를 기반으로 구한 값이 아닌 실제 빛 반사를 계산한 값을 리턴한다.
else
{
// ray의 방향벡터의 y 값을 기준으로 그라데이션을 주기 위한 계수.
t = 0.5 * (scene->ray.dir.y + 1.0);
// (1-t) * 흰색 + t * 하늘색
return (vplus(vmult(color3(1, 1, 1), 1.0 - t), vmult(color3(0.5, 0.7, 1.0), t)));
}
}phong_lighting.c
t_color3 phong_lighting(t_scene *scene)
{
t_color3 light_color;
t_object *lights;
light_color = color3(0, 0, 0);
lights = scene->light;
while (lights) // 존재하는 모든 광원들에 대한 정반사, 난반사 값을 연결리스트로 돌아가면서 구해준다.
{
if (lights->type == LIGHT_POINT)
light_color = vplus(light_color, point_light_get(scene, lights->element));
lights = lights->next;
}
// 정반사, 난반사 값을 더했다면 주변광을 더해준다.
light_color = vplus(light_color, scene->ambient);
return (vmin(vmult_(light_color, scene->rec.albedo), color3(1, 1, 1)));
// 이걸 왜 해주는데?
// 모든 광원에 의한 빛의 양을 구한 후, 오브젝트의 반사율과 곱해준다. 그 값이 (1, 1, 1)을 넘으면 (1, 1, 1)을 반환한다.
}주변광(Ambient) 적용
기본적으로 적용되는 빛.
main.c
t_scene *scene_init(void)
{
...
ka = 0.1;
scene->ambient = vmult(color3(1,1,1), ka); // 주변광(ambient), 기본적으로 들어가는 빛.
...
}이 부분에서 주변광이 설정하는데, ambient lighting의 색과 ambient lighting의 강도(ambient strength) 계수인 ka 의 곱으로 표현된다. ka는 [0 ~ 1] 사이의 값으로 설정된다.
phong_lighting.c
t_color3 phong_lighting(t_scene *scene)
{
t_color3 light_color;
t_object *lights;
light_color = color3(0, 0, 0);
lights = scene->light;
// while (lights) // 존재하는 모든 광원들에 대한 정반사, 난반사 값을 연결리스트로 돌아가면서 구해준다.
// {
// if (lights->type == LIGHT_POINT)
// light_color = vplus(light_color, point_light_get(scene, lights->element));
// lights = lights->next;
// }
// 정반사, 난반사 값을 더했다면 주변광(기본적으로 들어가는 빛, scene->ambient)을 더해준다.
light_color = vplus(light_color, scene->ambient);
return (vmin(vmult_(light_color, scene->rec.albedo), color3(1, 1, 1)));
// 모든 광원에 의한 빛의 양을 구한 후, 오브젝트의 반사율과 곱해준다. 그 값이 (1, 1, 1)을 넘으면 (1, 1, 1)을 반환한다.
}주변광만 적용하였을 때 결과는 다음처럼 나온다. 까맣게 보이는 것 같아도 도형의 원색인 빨간색, 초록색이 희미하게 보이는 것을 알 수 있다.

난반사(diffuse) 적용
광원에서 나온 빛이 직접 물체면에 부딪쳐 여러방향으로 확산되는 것을 표현한다.
교점에 도달한 빛의 양은 광원에서 출발한 빛 입자의 양을 도달한 교점의 면적(미소 면적)으로 나눈 값이다. 광원에서 출발한 빛 입자의 양은 항상 일정할 것이기 때문에, 빛이 도달한 미소 면적이 작을 수록 단위 면적당 도달한 빛 입자의 양은 많아질 것이고, 반대의 경우는 줄어들 것이다. 빛이 도달한 미소 면적이 가장 작을 때는 빛의 벡터가 교점의 법선 벡터와 일치할 때(사이각 0도)일 것이고, 사이각이 90도 이상이되면 미소 면적은 무한해지므로 빛 입자가 도달하지 못할 것이다.

두 벡터 사이의 각도는 벡터의 내적을 통해서 알 수 있다.
3차원 공간에서 벡터 두 개가 이루는 각을 cosθ(코사인세타)라고 할 때, 두 벡터의 내적을 구하는 수식은 다음과 같다.
이 때 두 벡터 A와 B가 크기가 1인 단위 벡터일 때, 내적의 결과는 사이각에 대한 코사인 값이 된다.
코사인과 사이각의 관계
다음 사이트에서 코사인 값과 사이각이 어떻게 서로 영향을 주는지 알 수 있다.
https://www.geogebra.org/m/XJsuYtVd
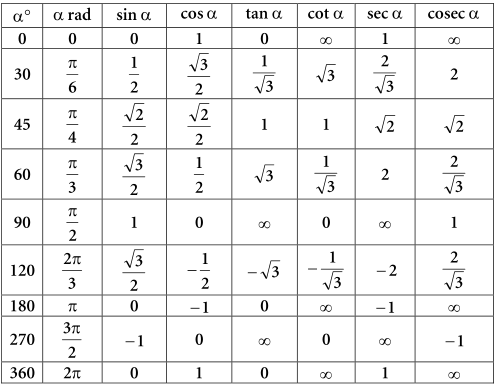
위의 표를 통해 우리는 코사인 값에 따라 사이각이 정해진다는 것을 유추할 수가 있게 된다.
즉, 단위 벡터끼리 내적 시의 사이각에 대해 알게 되는 것이다.
사이각 θ가 [0 ~ 90] 도 일 때, cosθ 값은 [1 ~ 0] 이므로, diffuse의 강도 계수인 kd를 cosθ 값으로 하게 될 것이다. 사이각이 0도라면 광원의 벡터와 표면적의 법선 벡터가 완벽하게 일치하는 수직이라는 의미이므로 빛이 가장 강하다고 할 수 있을 것이다.
이 난반사의 강도와 빛의 양을 곱해주면, 난반사를 통해 교점에 도달한 빛의 양을 계산할 수 있게 된다.
t_color3 point_light_get(t_scene *scene, t_light *light)
{
t_color3 diffuse;
t_vec3 light_dir;
double kd; // diffuse의 강도
light_dir = vunit(vminus(light->origin, scene->rec.p)); //교점에서 출발하여 광원을 향하는 벡터(정규화 됨)
// cosΘ는 Θ 값이 90도 일 때 0이고 Θ가 둔각이 되면 음수가 되므로 0.0보다 작은 경우는 0.0으로 대체한다.
kd = fmax(vdot(scene->rec.normal, light_dir), 0.0);// (교점에서 출발하여 광원을 향하는 벡터)와 (교점에서의 법선벡터)의 내적값.
// fmax 함수는 두 개의 인자 중 큰 값을 리턴한다. 만약 코사인세타가 둔각이 될 경우 음수가 되기에 0을 리턴하도록 한다.
diffuse = vmult(light->light_color, kd);
return (diffuse));
}주변광과 난반사를 적용했을 때의 결과는 다음처럼 된다. lights를 설정하는 코드에서 빛의 좌표를 바꾸면 도형도 해당 빛의 위치에 대응해서 빛을 반사한다.
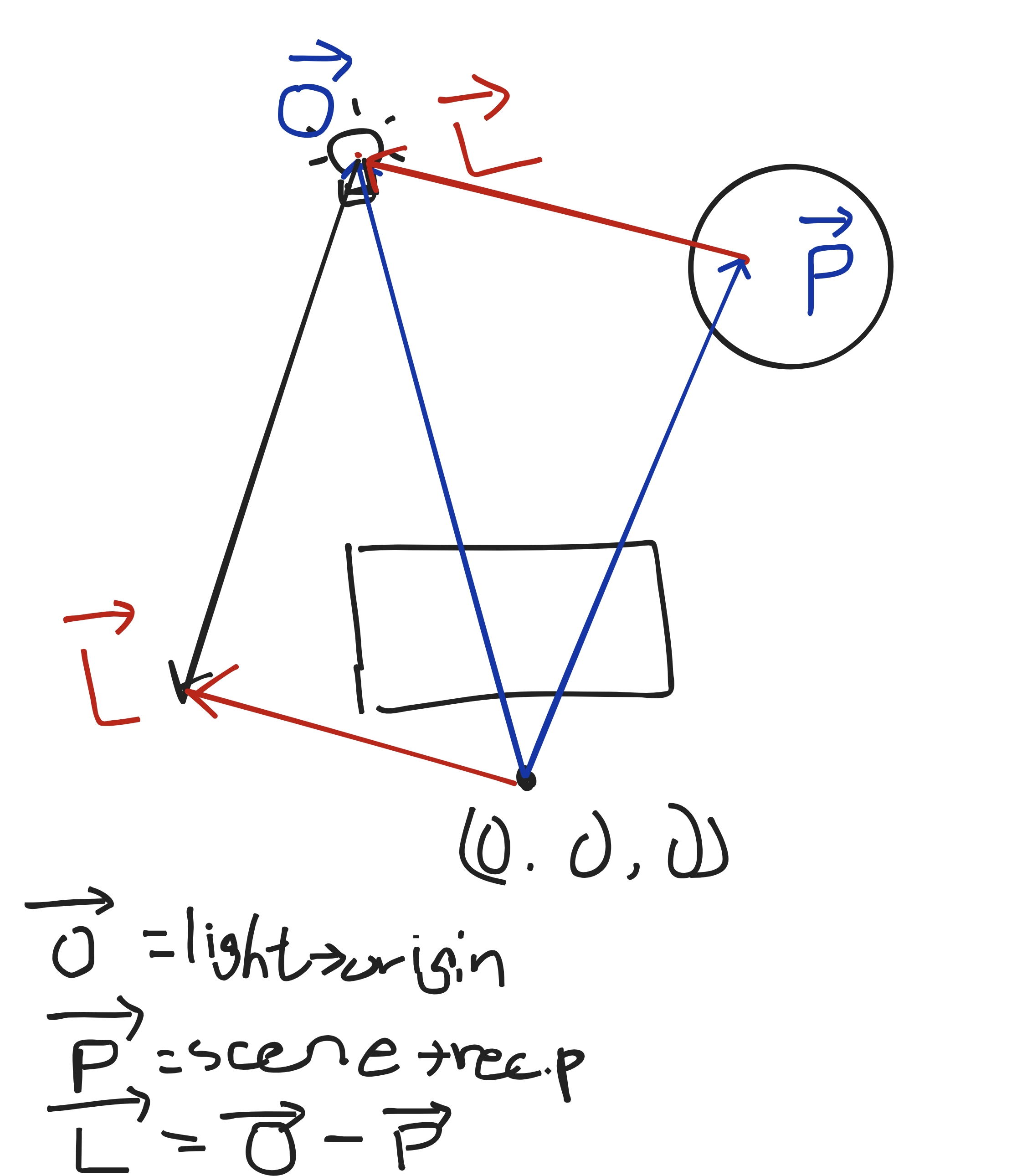
벡터 O는 light→origin, 벡터 P는 scene→rec.p, 벡터 L은 벡터 O - 벡터 P다.
- rec.p는 해당 광선(레이)가 뻗어나가면서 가장 먼저 마주친 물체의 교점에 대한 값이다.
- light->origin는 광원의 좌표이자 원점에서부터 해당 좌표를 향하는 벡터인데, 이 벡터에서 교점의 좌표이자 원점에서 해당 좌표를 향하는 벡터를 빼준다면 교점에서부터 광원을 향하는 벡터가 된다.
- light_dir은 벡터 L을 정규화시켜서 표준벡터로 만들어 준 것이다.
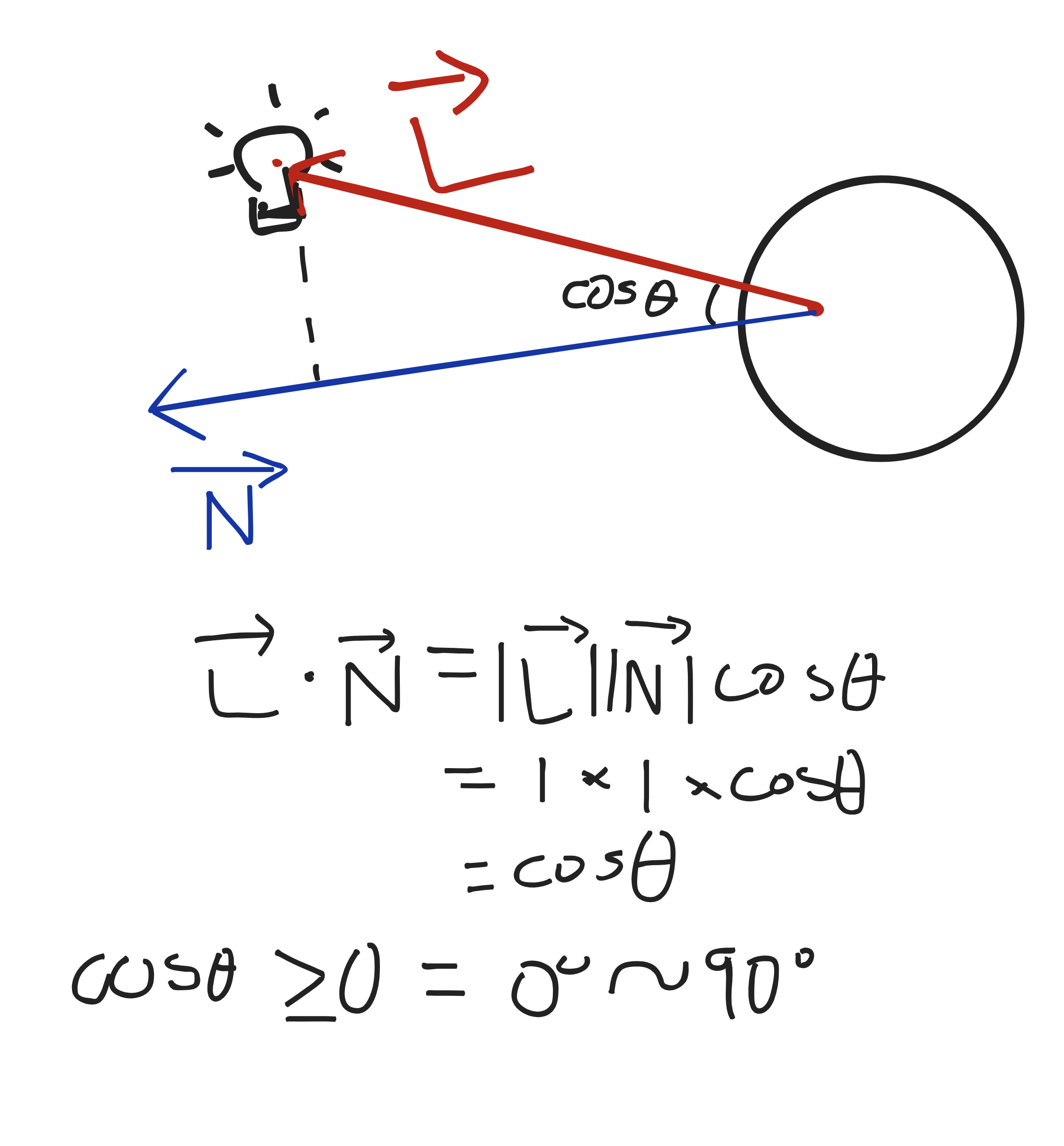
- scene->rec.normal는 충돌한 교점의 법선 벡터를 정규화한 것이다.
- 교점의 법선 벡터와 교점에서부터 광원으로 향하는 벡터를 내적하면 스칼라 값이 나오는데, 두 벡터 전부 단위 벡터이기에 이 값은 사이각에 대한 코사인 값이 된다.
- 위의 표에서도 나와있듯 코사인값에 따라 사이각이 얼마인지를 알 수 있게 된다.
- 사이각이 0도에 가까울 수록 빛을 정면으로 받고 있다는 의미가 된다.

정반사(specular) 적용
정반사는 특정 방향에서 바라볼 때에 광택이 나는 반질반질한 표면에서 반사되는 빛을 나타낸다.
specular의 값은 교점에서 카메라 원점을 향하는 벡터인 view_dir / **교점에서부터 광원까지의 표준벡터 light_dir를 대칭시킨 reflect_dir**의 사이각의 크기에 따른 코사인 값(spec 변수), 물체의 반짝거리는 정도를 나타내는 값인 shininess value(ksn 변수), [0 ~ 1] 사이의 임의의 값으로 설정하는 specular 강도(ks 변수)의 연산을 통해 결정된다.
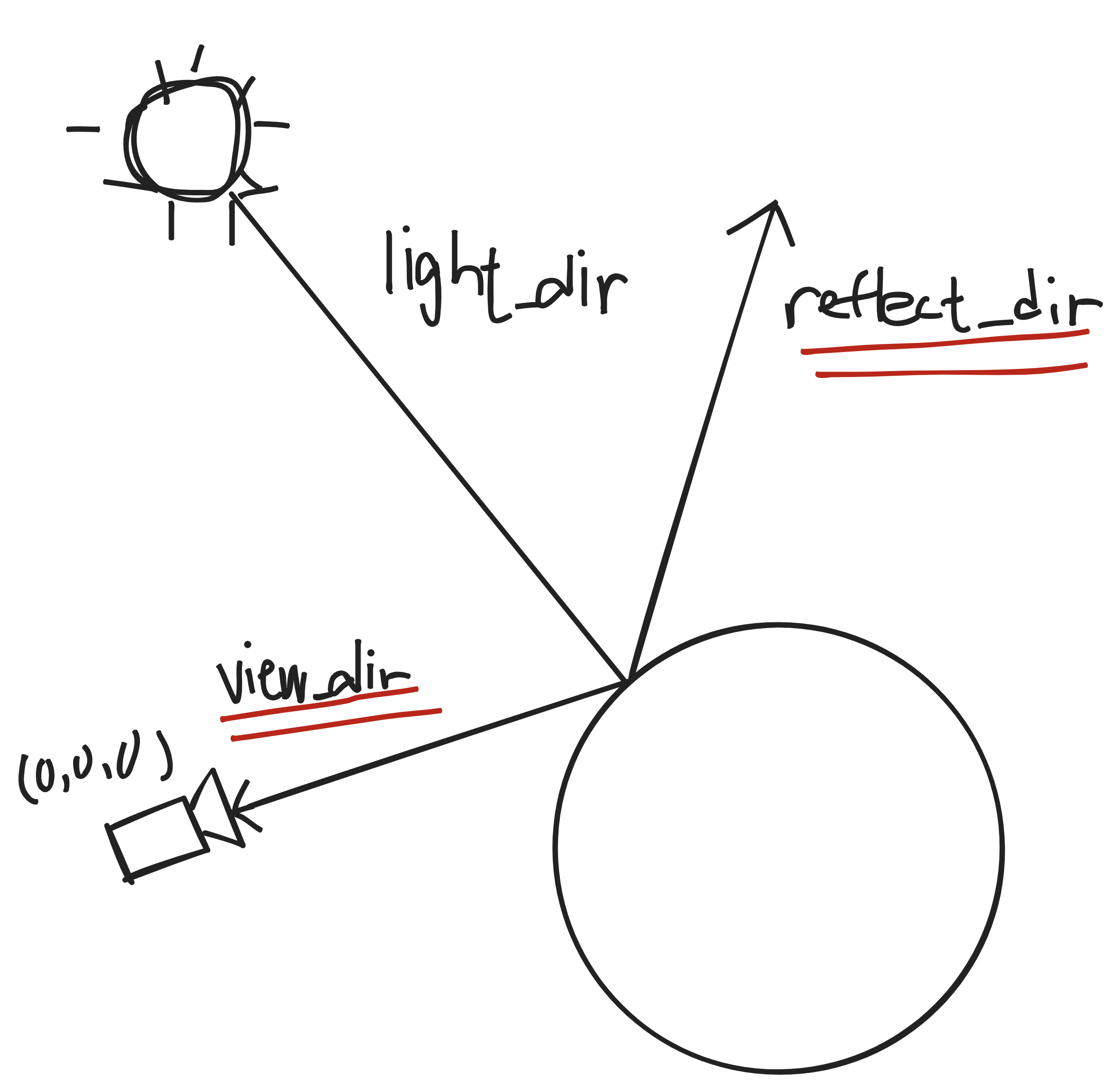
view_dir와 reflect_dir이 완전히 일치할 때(사이각 0도)가 정반사를 통해 카메라에 도달한 빛의 양이 가장 많을 것이고, 사이각이 커질 수록 정반사를 통해 카메라에 도달한 빛의 양은 줄어들 것이다. diffuse에서와 마찬가지로, 두 벡터(view_dir, reflect_dir)의 내적을 통해 cosθ 값을 구하고, 이 값을 spec으로 한다.
specular = spec
물체의 반짝거리는 정도를 표현하는 값인 Shininess value ksn 값은 앞서 계산한 spec에 지수로서 계산 된다. spec의 값은 [0 ~ 1] 사이의 실수 이므로 ksn 값이 커질 수록 물체의 하이라이팅 범위가 줄어든다(더 반짝거리는 물체)
specular = spec ^ ksn
마지막으로 specular의 강도 계수인 ks를 식에 곱해주면 specular 값을 얻게된다.
specular = ks * (spec ^ ksn)

코드로 구현하면 다음과 같다.
#include "trace.h"
t_vec3 reflect(t_vec3 v, t_vec3 n) // 반사광 벡터 구하기
{
double ray_light_dot; // 교점에서 카메라로 향하는 벡터 v와 교점의 법선 벡터 N를 내적한 스칼라 값
t_vec3 dot_vec;
t_vec3 reverse_v; // 벡터 V를 반대방향으로 돌린 것, 역벡터
ray_light_dot = vdot(v, n); // 벡터 V와 벡터 N를 내적한 값.
dot_vec = vmult(n, ray_light_dot * 2); // 내적한 값을 벡터화 시킨것 (벡터 N이 단위 벡터이기에 가능)
// 2를 곱해주는 이유는 벡터 V를 역벡터화시켰기 때문.
reverse_v = vmult(v, -1);
return (vplus(reverse_v, dot_vec));
}
t_color3 point_light_get(t_scene *scene, t_light *light)
{
t_color3 diffuse;
t_vec3 light_dir; // 빛의 방향 벡터
double kd; // 난반사의 강도
t_color3 specular;
t_vec3 view_dir; // 카메라 원점을 향하는 벡터
t_vec3 reflect_dir; // 법전을 기준으로 광선의 벡터를 대칭시킨 벡터
double spec; // 사이각의 크기에 따른 코사인 값
double ksn; // 반짝거리는 정도
double ks; //
light_dir = vunit(vminus(light->origin, scene->rec.p)); //교점에서 출발하여 광원을 향하는 벡터(정규화)
// rec.p는 해당 광선(레이)가 뻗어나가면서 가장 먼저 마주친 물체의 교점에 대한 값이다.
// cosΘ는 Θ 값이 90도 일 때 0이고 Θ가 둔각이 되면 음수가 되므로 0.0보다 작은 경우는 0.0으로 대체한다.
kd = fmax(vdot(scene->rec.normal, light_dir), 0.0);// (교점에서 출발하여 광원을 향하는 벡터)와 (교점에서의 법선벡터)의 내적값.
// fmax 함수는 두 개의 인자 중 큰 값을 리턴한다. 만약 코사인세타가 둔각이 될 경우 음수가 되기에 0을 리턴하도록 한다.
diffuse = vmult(light->light_color, kd);
view_dir = vunit(vmult(scene->ray.dir, -1));
reflect_dir = reflect(light_dir, scene->rec.normal);
ksn = 30; // 작을 수록 정반사를 받는 범위는 늘어나지만 빛의 세기는 약해진다.
ks = 0.8; // 정반사의 강도
spec = pow(fmax(vdot(view_dir, reflect_dir), 0.0), ksn);
specular = vmult(vmult(light->light_color, ks), spec);
return (vplus(diffuse, specular));
}
t_color3 phong_lighting(t_scene *scene)
{
t_color3 light_color;
t_object *lights;
light_color = color3(0, 0, 0);
lights = scene->light;
while (lights) // 존재하는 모든 광원들에 대한 정반사, 난반사 값을 연결리스트로 돌아가면서 구해준다.
{
if (lights->type == LIGHT_POINT)
light_color = vplus(light_color, point_light_get(scene, lights->element));
lights = lights->next;
}
// 정반사, 난반사 값을 더했다면 주변광(기본적으로 들어가는 빛, scene->ambient)을 더해준다.
light_color = vplus(light_color, scene->ambient);
return (vmin(vmult_(light_color, scene->rec.albedo), color3(1, 1, 1)));
// 모든 광원에 의한 빛의 양을 구한 후, 오브젝트의 반사율과 곱해준다. 그 값이 (1, 1, 1)을 넘으면 (1, 1, 1)을 반환한다.
}레퍼런스
mini_raytracing_in_c/08.phong_lighting.md at main · GaepoMorningEagles/mini_raytracing_in_c
